{ "cells": [ { "cell_type": "code", "execution_count": 1, "metadata": { "tags": [ "remove_input" ] }, "outputs": [], "source": [ "path_data = '../../../../data/'\n", "\n", "import numpy as np\n", "import pandas as pd\n", "import math\n", "import scipy.stats as stats\n", "\n", "%matplotlib inline\n", "import matplotlib.pyplot as plt\n", "from mpl_toolkits.mplot3d import Axes3D\n", "plt.style.use('fivethirtyeight')\n", "\n", "import warnings\n", "warnings.filterwarnings('ignore')" ] }, { "cell_type": "code", "execution_count": 2, "metadata": { "tags": [ "remove_input" ] }, "outputs": [], "source": [ "\n", "def distance(point1, point2):\n", " \"\"\"Returns the distance between point1 and point2\n", " where each argument is an array \n", " consisting of the coordinates of the point\"\"\"\n", " return np.sqrt(np.sum((point1 - point2)**2))\n", "\n", "def all_distances(training, new_point):\n", " \"\"\"Returns an array of distances\n", " #between each point in the training set\n", " #and the new point (which is a row of attributes)\"\"\"\n", " attributes = training.drop(columns=['Class'])\n", " def distance_from_point(row):\n", " return distance(new_point, np.array(row)) # --- possible issue as original = np.array(new_point)\n", " return attributes.apply(distance_from_point, axis=1)\n", "\n", "def table_with_distances(training, new_point):\n", " \"\"\"Augments the training table \n", " with a column of distances from new_point\"\"\"\n", " training1 = training.copy()\n", " training1['Distance'] = all_distances(training1, new_point)\n", " return training1\n", "\n", "def closest(training, new_point, k):\n", " \"\"\"Returns a table of the k rows of the augmented table\n", " corresponding to the k smallest distances\"\"\"\n", " with_dists = table_with_distances(training, new_point)\n", " sorted_by_distance = with_dists.sort_values(by=['Distance'])\n", " topk = sorted_by_distance.take(np.arange(k))\n", " return topk\n", "\n", "def majority(topkclasses):\n", " ones = len(topkclasses[topkclasses['Class'] == 1])\n", " zeros = len(topkclasses[topkclasses['Class'] == 0])\n", " if ones > zeros:\n", " return 1\n", " else:\n", " return 0\n", "\n", "def classify(training, new_point, k):\n", " closestk = closest(training, new_point, k)\n", " topkclasses = closestk[['Class']]\n", " return majority(topkclasses)" ] }, { "cell_type": "code", "execution_count": 3, "metadata": { "tags": [ "remove_input" ] }, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
ClassAlcoholMalic AcidAshAlcalinity of AshMagnesiumTotal PhenolsFlavanoidsNonflavanoid phenolsProanthocyaninsColor IntensityHueOD280/OD315 of diulted winesProline
0114.231.712.4315.61272.803.060.282.295.641.043.921065
1113.201.782.1411.21002.652.760.261.284.381.053.401050
2113.162.362.6718.61012.803.240.302.815.681.033.171185
3114.371.952.5016.81133.853.490.242.187.800.863.451480
4113.242.592.8721.01182.802.690.391.824.321.042.93735
\n", "
" ], "text/plain": [ " Class Alcohol Malic Acid Ash Alcalinity of Ash Magnesium \\\n", "0 1 14.23 1.71 2.43 15.6 127 \n", "1 1 13.20 1.78 2.14 11.2 100 \n", "2 1 13.16 2.36 2.67 18.6 101 \n", "3 1 14.37 1.95 2.50 16.8 113 \n", "4 1 13.24 2.59 2.87 21.0 118 \n", "\n", " Total Phenols Flavanoids Nonflavanoid phenols Proanthocyanins \\\n", "0 2.80 3.06 0.28 2.29 \n", "1 2.65 2.76 0.26 1.28 \n", "2 2.80 3.24 0.30 2.81 \n", "3 3.85 3.49 0.24 2.18 \n", "4 2.80 2.69 0.39 1.82 \n", "\n", " Color Intensity Hue OD280/OD315 of diulted wines Proline \n", "0 5.64 1.04 3.92 1065 \n", "1 4.38 1.05 3.40 1050 \n", "2 5.68 1.03 3.17 1185 \n", "3 7.80 0.86 3.45 1480 \n", "4 4.32 1.04 2.93 735 " ] }, "execution_count": 3, "metadata": {}, "output_type": "execute_result" } ], "source": [ "wine = pd.read_csv(path_data + 'wine.csv')\n", "\n", "# For converting Class to binary\n", "\n", "def is_one(x):\n", " if x == 1:\n", " return 1\n", " else:\n", " return 0\n", "\n", "wine['Class1'] = wine['Class'].apply(is_one)\n", "\n", "# This creates a column 'Class1' - we drop the 'Class' column, rename 'Class1' as 'Class'\n", "# then move the column to the first position using 'pop' and 'insert'\n", "\n", "wine = wine.drop(columns=['Class'])\n", "\n", "wine = wine.rename(columns={'Class1': 'Class'})\n", "\n", "class_label = wine.pop('Class')\n", "\n", "wine.insert(0, 'Class', class_label)\n", "\n", "wine.head(5)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### The Accuracy of the Classifier ###\n", "To see how well our classifier does, we might put 50% of the data into the training set and the other 50% into the test set. Basically, we are setting aside some data for later use, so we can use it to measure the accuracy of our classifier. We've been calling that the *test set*. Sometimes people will call the data that you set aside for testing a *hold-out set*, and they'll call this strategy for estimating accuracy the *hold-out method*.\n", "\n", "Note that this approach requires great discipline. Before you start applying machine learning methods, you have to take some of your data and set it aside for testing. You must avoid using the test set for developing your classifier: you shouldn't use it to help train your classifier or tweak its settings or for brainstorming ways to improve your classifier. Instead, you should use it only once, at the very end, after you've finalized your classifier, when you want an unbiased estimate of its accuracy." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Measuring the Accuracy of Our Wine Classifier ###\n", "OK, so let's apply the hold-out method to evaluate the effectiveness of the $k$-nearest neighbor classifier for identifying wines. The data set has 178 wines, so we'll randomly permute the data set and put 89 of them in the training set and the remaining 89 in the test set." ] }, { "cell_type": "code", "execution_count": 4, "metadata": {}, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
ClassAlcoholMalic AcidAshAlcalinity of AshMagnesiumTotal PhenolsFlavanoidsNonflavanoid phenolsProanthocyaninsColor IntensityHueOD280/OD315 of diulted winesProline
50113.051.732.0412.4922.723.270.172.917.201.122.911150
131012.882.992.4020.01041.301.220.240.835.400.741.42530
136012.254.722.5421.0891.380.470.530.803.850.751.27720
110011.463.741.8219.51073.182.580.243.582.900.752.81562
130012.861.352.3218.01221.511.250.210.944.100.761.29630
\n", "
" ], "text/plain": [ " Class Alcohol Malic Acid Ash Alcalinity of Ash Magnesium \\\n", "50 1 13.05 1.73 2.04 12.4 92 \n", "131 0 12.88 2.99 2.40 20.0 104 \n", "136 0 12.25 4.72 2.54 21.0 89 \n", "110 0 11.46 3.74 1.82 19.5 107 \n", "130 0 12.86 1.35 2.32 18.0 122 \n", "\n", " Total Phenols Flavanoids Nonflavanoid phenols Proanthocyanins \\\n", "50 2.72 3.27 0.17 2.91 \n", "131 1.30 1.22 0.24 0.83 \n", "136 1.38 0.47 0.53 0.80 \n", "110 3.18 2.58 0.24 3.58 \n", "130 1.51 1.25 0.21 0.94 \n", "\n", " Color Intensity Hue OD280/OD315 of diulted wines Proline \n", "50 7.20 1.12 2.91 1150 \n", "131 5.40 0.74 1.42 530 \n", "136 3.85 0.75 1.27 720 \n", "110 2.90 0.75 2.81 562 \n", "130 4.10 0.76 1.29 630 " ] }, "execution_count": 4, "metadata": {}, "output_type": "execute_result" } ], "source": [ "shuffled_wine = wine.sample(len(wine), replace=False) \n", "training_set = shuffled_wine.take(np.arange(89))\n", "training_set.head()" ] }, { "cell_type": "code", "execution_count": 5, "metadata": {}, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
ClassAlcoholMalic AcidAshAlcalinity of AshMagnesiumTotal PhenolsFlavanoidsNonflavanoid phenolsProanthocyaninsColor IntensityHueOD280/OD315 of diulted winesProline
150013.503.122.6224.01231.401.570.221.258.600.591.30500
117012.421.612.1922.51082.002.090.341.612.061.062.96345
98012.371.072.1018.5883.523.750.241.954.501.042.77660
140012.932.812.7021.0961.540.500.530.754.600.772.31600
129012.044.302.3822.0802.101.750.421.352.600.792.57580
\n", "
" ], "text/plain": [ " Class Alcohol Malic Acid Ash Alcalinity of Ash Magnesium \\\n", "150 0 13.50 3.12 2.62 24.0 123 \n", "117 0 12.42 1.61 2.19 22.5 108 \n", "98 0 12.37 1.07 2.10 18.5 88 \n", "140 0 12.93 2.81 2.70 21.0 96 \n", "129 0 12.04 4.30 2.38 22.0 80 \n", "\n", " Total Phenols Flavanoids Nonflavanoid phenols Proanthocyanins \\\n", "150 1.40 1.57 0.22 1.25 \n", "117 2.00 2.09 0.34 1.61 \n", "98 3.52 3.75 0.24 1.95 \n", "140 1.54 0.50 0.53 0.75 \n", "129 2.10 1.75 0.42 1.35 \n", "\n", " Color Intensity Hue OD280/OD315 of diulted wines Proline \n", "150 8.60 0.59 1.30 500 \n", "117 2.06 1.06 2.96 345 \n", "98 4.50 1.04 2.77 660 \n", "140 4.60 0.77 2.31 600 \n", "129 2.60 0.79 2.57 580 " ] }, "execution_count": 5, "metadata": {}, "output_type": "execute_result" } ], "source": [ "test_set = shuffled_wine.take(np.arange(89, 178))\n", "test_set.head()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "We'll train the classifier using the 89 wines in the training set, and evaluate how well it performs on the test set. To make our lives easier, we'll write a function to evaluate a classifier on every wine in the test set:" ] }, { "cell_type": "code", "execution_count": 6, "metadata": {}, "outputs": [], "source": [ "def count_zero(array):\n", " \"\"\"Counts the number of 0's in an array\"\"\"\n", " return len(array) - np.count_nonzero(array)\n", "\n", "def count_equal(array1, array2):\n", " \"\"\"Takes two numerical arrays of equal length\n", " and counts the indices where the two are equal\"\"\"\n", " return count_zero(array1 - array2)\n", "\n", "def evaluate_accuracy(training, test, k):\n", " test_attributes = test.drop(columns=['Class'])\n", " def classify_testrow(row):\n", " return classify(training, row, k)\n", " c = test_attributes.apply(classify_testrow, axis=1)\n", " return count_equal(c, test['Class']) / len(test)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Now for the grand reveal -- let's see how we did. We'll arbitrarily use $k=5$." ] }, { "cell_type": "code", "execution_count": 7, "metadata": {}, "outputs": [ { "data": { "text/plain": [ "0.898876404494382" ] }, "execution_count": 7, "metadata": {}, "output_type": "execute_result" } ], "source": [ "evaluate_accuracy(training_set, test_set, 5)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The accuracy rate isn't bad at all for a simple classifier." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Breast Cancer Diagnosis ###\n", "\n", "Now I want to do an example based on diagnosing breast cancer. I was inspired by Brittany Wenger, who won the Google national science fair in 2012 a 17-year old high school student. Here's Brittany:\n", "\n", "![Brittany Wenger](http://i.huffpost.com/gen/701499/thumbs/o-GSF83-570.jpg?3)\n", "\n", "Brittany's [science fair project](https://sites.google.com/a/googlesciencefair.com/science-fair-2012-project-64a91af142a459cfb486ed5cb05f803b2eb41354-1333130785-87/home) was to build a classification algorithm to diagnose breast cancer. She won grand prize for building an algorithm whose accuracy was almost 99%. \n", "\n", "Let's see how well we can do, with the ideas we've learned in this course.\n", "\n", "So, let me tell you a little bit about the data set. Basically, if a woman has a lump in her breast, the doctors may want to take a biopsy to see if it is cancerous. There are several different procedures for doing that. Brittany focused on fine needle aspiration (FNA), because it is less invasive than the alternatives. The doctor gets a sample of the mass, puts it under a microscope, takes a picture, and a trained lab tech analyzes the picture to determine whether it is cancer or not. 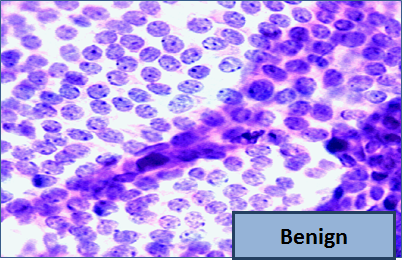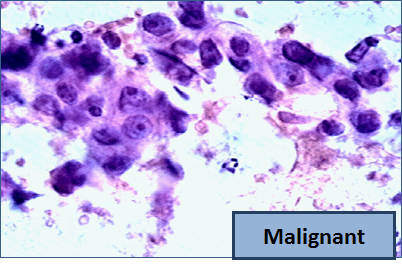We get a picture like one of the following:\n", "\n", "![benign](benign.png)\n", "\n", "![cancer](malignant.png)\n", "\n", "Unfortunately, distinguishing between benign vs malignant can be tricky. So, researchers have studied the use of machine learning to help with this task. The idea is that we'll ask the lab tech to analyze the image and compute various attributes: things like the typical size of a cell, how much variation there is among the cell sizes, and so on. Then, we'll try to use this information to predict (classify) whether the sample is malignant or not. We have a training set of past samples from women where the correct diagnosis is known, and we'll hope that our machine learning algorithm can use those to learn how to predict the diagnosis for future samples.\n", "\n", "We end up with the following data set. For the \"Class\" column, 1 means malignant (cancer); 0 means benign (not cancer)." ] }, { "cell_type": "code", "execution_count": 8, "metadata": {}, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
Clump ThicknessUniformity of Cell SizeUniformity of Cell ShapeMarginal AdhesionSingle Epithelial Cell SizeBare NucleiBland ChromatinNormal NucleoliMitosesClass
05111213110
154457103210
23111223110
36881343710
44113213110
.................................
6783111321110
6792111211110
6805101037381021
68148643410611
68248854510411
\n", "

683 rows × 10 columns

\n", "
" ], "text/plain": [ " Clump Thickness Uniformity of Cell Size Uniformity of Cell Shape \\\n", "0 5 1 1 \n", "1 5 4 4 \n", "2 3 1 1 \n", "3 6 8 8 \n", "4 4 1 1 \n", ".. ... ... ... \n", "678 3 1 1 \n", "679 2 1 1 \n", "680 5 10 10 \n", "681 4 8 6 \n", "682 4 8 8 \n", "\n", " Marginal Adhesion Single Epithelial Cell Size Bare Nuclei \\\n", "0 1 2 1 \n", "1 5 7 10 \n", "2 1 2 2 \n", "3 1 3 4 \n", "4 3 2 1 \n", ".. ... ... ... \n", "678 1 3 2 \n", "679 1 2 1 \n", "680 3 7 3 \n", "681 4 3 4 \n", "682 5 4 5 \n", "\n", " Bland Chromatin Normal Nucleoli Mitoses Class \n", "0 3 1 1 0 \n", "1 3 2 1 0 \n", "2 3 1 1 0 \n", "3 3 7 1 0 \n", "4 3 1 1 0 \n", ".. ... ... ... ... \n", "678 1 1 1 0 \n", "679 1 1 1 0 \n", "680 8 10 2 1 \n", "681 10 6 1 1 \n", "682 10 4 1 1 \n", "\n", "[683 rows x 10 columns]" ] }, "execution_count": 8, "metadata": {}, "output_type": "execute_result" } ], "source": [ "patients = pd.read_csv(path_data + 'breast-cancer.csv').drop(columns=['ID'])\n", "patients" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "So we have 9 different attributes. I don't know how to make a 9-dimensional scatterplot of all of them, so I'm going to pick two and plot them:" ] }, { "cell_type": "code", "execution_count": 9, "metadata": {}, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
ClassClump ThicknessUniformity of Cell SizeUniformity of Cell ShapeMarginal AdhesionSingle Epithelial Cell SizeBare NucleiBland ChromatinNormal NucleoliMitosesColor
00511121311gold
105445710321gold
20311122311gold
\n", "
" ], "text/plain": [ " Class Clump Thickness Uniformity of Cell Size Uniformity of Cell Shape \\\n", "0 0 5 1 1 \n", "1 0 5 4 4 \n", "2 0 3 1 1 \n", "\n", " Marginal Adhesion Single Epithelial Cell Size Bare Nuclei \\\n", "0 1 2 1 \n", "1 5 7 10 \n", "2 1 2 2 \n", "\n", " Bland Chromatin Normal Nucleoli Mitoses Color \n", "0 3 1 1 gold \n", "1 3 2 1 gold \n", "2 3 1 1 gold " ] }, "execution_count": 9, "metadata": {}, "output_type": "execute_result" } ], "source": [ "color_table = pd.DataFrame(\n", " {'Class':np.array([1, 0]),\n", " 'Color':np.array(['darkblue', 'gold'])}\n", ")\n", "patients_with_colors = pd.merge(patients, color_table, on='Class')\n", "\n", "patent_label = patients_with_colors.pop('Class')\n", "\n", "patients_with_colors.insert(0, 'Class', patent_label)\n", "\n", "patients_with_colors.head(3)" ] }, { "cell_type": "code", "execution_count": 10, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAqkAAAGTCAYAAAALL4uRAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Il7ecAAAACXBIWXMAAAsTAAALEwEAmpwYAABaaElEQVR4nO3deVhUZf8G8PsAAirIACriAiLgvi+5i0uvSu6iuWaZAWL2e80Vk/TV3Nd8sUjRTMvcF1wyy1RC1BLT1EoDUUQBF2BAVFCc+f3By+gwMzjIwHlo7s91eeV8z5kzt88Z4+s55zlHUiqVahARERERCcRC7gBERERERAWxSSUiIiIi4bBJJSIiIiLhsEklIiIiIuGwSSUiIiIi4bBJJSIiIiLhsEklIiIiIuGwSSUAQGxsrNwRyjSOX/Fw/F4dx654OH5E4mKTSkRERETCYZNKRERERMJhk0pEREREwmGTSkRERETCsZI7ABEREcknNzcXDx8+lDsGmaGKFSvCyspwK8omlYiIyEzl5ubiwYMHUCgUkCRJ7jhkRtRqNZRKJezt7Q02qjzdT0REZKYePnzIBpVkIUkSFApFoUfx2aQSERGZMTaoJJeXfffYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIREZFZ2rJlC2rUqCF3DABAaGgomjRpUuztREVFQaFQIDU1Ve/yhIQEKBQKnD9/3uA2jFmnNLBJJSIiojLp7t27mDFjBpo3b46qVauiQYMGGDJkCH744Qe5o5EJ8D6pREREVOYkJCSgd+/esLOzw5w5c9C4cWOoVCpERkZi8uTJuHz5cqnkePLkCaytrUvls17myZMnckcwKR5JJSIiomJJSMiEv/8x9O17EP7+x5CQkFninzl16lSo1WocP34cgwYNgre3N+rVq4eAgACcPHkSAJCYmIhRo0ahZs2aqFmzJkaPHo3bt28Xut2NGzeiRYsWqFKlClq0aIFNmzZpLVcoFAgPD8fo0aNRvXp1zJs375Xyr169GnXr1kWNGjUQGBiIrKwsreW//fYbBg0ahDp16qBWrVro3bs3fv311yJnycnJwahRo9ClSxfcu3dPU4+Li0Pv3r3h4uKCNm3a4NixYwaz6ruEQN8lAVeuXMGbb76JmjVrwsvLC+PGjcOdO3eKPDb52KQSERHRK0tIyMTAgYexc+c1nDyZjJ07r2HgwMMl2qimp6fj6NGj8Pf3h52dnc5yhUIBtVqNUaNG4d69e9i/fz8OHDiAlJQUjBo1Cmq1Wu92Dxw4gGnTpiEoKAinT5/G+PHjMWXKFBw+fFhrvSVLlqBnz544deoU3nvvPQBAjRo1Cv01ZMgQzfv37t2L+fPnY+bMmYiMjIS3tzc+//xzrc948OABhg0bhsOHD+Onn35CkyZNMHToUJ1rTfVlyZeZmQk/Pz+kp6fj4MGDqFKlimbZnDlzEBgYiKioKHTt2hUjR45EUlKSEaOvX0pKCt544w00aNAAP/30E/bt24esrCyMGDECKpXqlbbJ0/1ERET0yubPj8H169oN6fXrmZg/Pwbh4d1L5DPj4+OhVqtRt25dg+ucOHECly9fxvnz5+Hu7g4AWL9+PVq0aIHIyEh07dpV5z1r1qzBsGHDEBAQAADw8vLChQsXsHr1avj6+mrWGzRoEMaMGaP13qioqEIz29raan4fFhaGESNGYOzYsQDyjgpHRUUhPj5es46Pj4/W+5cuXYr9+/fj6NGjGDZsmMEsiYmJAID79+8jICAArq6u+Oqrr7Q+HwDeffddDBo0CEBeo3vs2DF8+eWXCAkJKfTPYciGDRvQuHFjzJ07V1Nbu3YtateujfPnz6NVq1ZF3iabVCIiInplycmP9NZTUvTXTcHQkdAXXb16Fa6urpoGFQBq164NV1dXXLlyRW+TevXqVYwaNUqr1r59e50jqS1atNB5b506dYxMn/c5b731llatTZs2Wk3qvXv3sGDBAkRFReHevXt49uwZHj9+jFu3br00CwAMHjwYTZs2xddffw0rK912r02bNprfW1hYoFWrVrhy5YrRf4aCfv/9d5w6dUrv3RKuX7/OJpWIiIhKl6trBb31atX0103B09MTkiTh77//NriOWq02+NjNwh7HqW9ZwVrFihV11nnZrazat2+PXbt2FbrOi4KCgnD37l0sXLgQbm5usLGxQf/+/XUmR+nLAgC9evXC3r178ccff6BZs2ZGf64+FhZ5V4e++I+D3NxcrXVUKhV69uyJ+fPn67z/xcsMioJNKhEREb2ykJDWiIm5p3XK38OjEkJCWpfYZzo6OqJHjx4IDw9HYGCgznWpSqUS9evXR1JSEhISEjRHU2/cuIHk5GTUr19f73br1auHM2fOaB3lPH36tMH1X1SU0/316tVDTEyM1ufExMRorX/mzBksXrwYvXr1ApB3u62iTEKaNWsWHB0dMXDgQERERKBp06Zay2NiYjSXFKjVavz2228YMGCA3m1VrlwZQN51p/m/v3TpktY6zZo1w969e1GrVi2UK1fO6JyFYZNKREREr8zdvRL27fPF/PkxSEl5hGrVKiAkpDXc3SuV6OcuX74cvXr1Qrdu3TBr1iw0atQIarUaUVFRWLVqFS5duoTGjRsjICAAS5YsgVqtxvTp09GsWTN06dJF7zY/+OADvPPOO2jevDm6d++Oo0ePYufOnfj6669fmqcop/vHjx+P8ePHo2XLlujUqRMiIiJw7tw5KBQKzTqenp7YsWMHWrdujUePHmH27NlFvtXVxx9/DLVarWlUX3xYwJdffgkvLy80bNgQ69evR2JiIt59912Df7aaNWti8eLF+M9//oObN29i2bJlWuu899572LRpE8aOHYtJkyahcuXKuHHjhmaSmL29fZGyA2xSiYiIqJjc3SuV2CQpQ2rXro3IyEisWLECc+bMQXJyMpycnNC4cWOsWrUKkiRhy5YtmDFjBvr27QsgbzLS0qVLDZ7u79u3L5YuXYrQ0FDMnDkTtWrVwooVK7QmTZnC4MGDcePGDXzyySd4/PgxfH19MWHCBHz77beaddasWYNJkyaha9euqFatGoKDgw0+Raows2fPhlqtxoABAxAREYFKlfL+8TBnzhx89tln+P3331GrVi188803Bi9ZKFeuHDZs2IApU6agU6dOaNKkCWbPnq01gcvV1RVHjhzB3Llz4efnh5ycHNSsWRPdunWDjY1NkXMDgKRUKl9+9TH948XGxsLb21vuGGUWx694OH6vjmNXPOY+fhkZGXBwcJA7Bpmxwr6DvE8qEREREQmHTSoRERERCYdNKhEREREJR9YmNTo6GsOHD0eDBg2gUCiwZcsWreVqtRqLFi1C/fr1Ua1aNfTp0wd//fWXTGlfjZSbgPLp/qh4vy/Kp/tDyk2QO5KW/Octjx9/vtSet1wUCxachaNjOBSKcDg6hmPBgrNyR9Kye3ccqlffiLZtT6B69Y3YvTtO7kha8vM5O4cLmU9kon/38vO1aXNCyHyif/dEHz8ikrlJffjwIRo2bIjFixejfPnyOstXr16Nzz77TPO4ripVqmDQoEF48OCBDGmLTspNQMW0gbDO3gmrpydhnb0TFdMGCtOovvi85XPnMkrlectFsWDBWSxbdgH59w5Wq4Flyy4I88Nk9+44jBt3HI8e5UKlAh49ysW4cceF+WH8Yr5nz8TLJzLRv3ui5xP9uyf6+BFRHmFm99eoUQNLly7VPI5MrVajfv368Pf3x9SpUwEAjx8/hre3Nz755BPN825FVj7dH9bZO3XqT2yH4rFjuAyJtPn7H8POndd06kOHepb6rUT0cXQMh74n30kSkJ7uX/qBCqhefSMePcrVqVeoYIWkJPm/n6Lne5FoM6xF/+6Jnk/0757o41eaOLuf5FbYd1DY+6QmJCTgzp076N79ebNUvnx5dOjQAb/88ovBJjU2Nra0Ir5UXdt4WOsZ4eyseMTelz9nfPx9A/VUIcbR0KOZ1Wox9nN2tu4P4fw68xWdSJlE/+6Jnk/0757o45dPpH+4EclB2CY1/9FfBZ/3WqVKFSQnJxt8n0h/qW3T6wDZ53TrdnXgXUv+nHXqJOLcuQw9dWchxlGSThg82iFCPlvbk3qPFtnaWjFfEYl2JFX0757o+UT/7ok+fkSUR/jZ/QWfCqFWqw0+KUI02fYheGbpoVV7ZumBbPsQmRJpCwlpDQ8P7cfWlfTzloti6tTmRaqXttDQzkWqlzbR84lM9O+e6PlE/+6JPn5ElEfYJtXFxQUAcPfuXa36/fv3dY6uikpt5Y6HTvvwxHYocst1xhPboXjotA9qK3e5owF4/rzloUM90aqVAkOHemLfPt8Sf96ysWbNaoNp05oj/98kkgRMm9Ycs2a1kTfY//j5eWHDhm6oUMEKFhZ519tt2NANfn5eckcDoJ3P0lK8fCIT/bsnej7Rv3uijx+Vni1bthh8FGhZoFAoEBERYXB5amoqFAoFoqKiSjGV6Qg/cSogIABTpkwBAGRnZ8Pb2xvz5s0rExOnyhLRTreWNRy/4uH4vTqOXfGY+/iV9YlTd+/exYoVK3DkyBEkJSXB2dkZjRo1QkBAAHr27PnS92/ZsgXTp0/H7du3SyGt6SkUCmzatAkDBgzQuzw1NRWenp44cOAAOncW40xGQcJOnMrKykJ8fDwAQKVS4datW7h48SIcHR1Rq1YtBAUFYcWKFfD29oaXlxeWL1+OihUrYsiQIXLGJiIiIpklJCSgd+/esLOzw5w5c9C4cWOoVCpERkZi8uTJuHz5cqnkePLkCaytrUvls8yNrKf7z58/jy5duqBLly54/PgxFi1ahC5dumDhwoUAgH//+9+YMGECpk2bhm7duiElJQV79uyBvb29nLGJiIjoBXI8uGbq1KlQq9U4fvw4Bg0aBG9vb9SrVw8BAQE4efIkACAxMRGjRo1CzZo1UbNmTYwePfqlR003btyIFi1aoEqVKmjRogU2bdqktVyhUCA8PByjR49G9erVMW/evFfKv3LlSnh7e6NGjRoIDAzE4sWL0aRJE81ylUqFpUuXolGjRqhatSo6dOiAQ4cOFbrN3377DT4+PnBxcUHnzp0RExPzStlEIeuR1M6dO0OpVBpcLkkSZs6ciZkzZ5ZeKCIiIjJa/oNrLJ9dzys8BSyfxpToHIz09HQcPXoUISEhsLOz01muUCigVqsxatQo2NraYv/+/ZAkCdOmTcOoUaNw/PhxvZOwDxw4gGnTpmHhwoXo3r07fvrpJ0yZMgVVq1aFr6+vZr0lS5Zg9uzZmD9/vqb2smtb27dvj127dgEAdu/ejSVLlmDZsmXo0KED9u/fj08//VTrtHdYWBhCQ0OxcuVKtGjRAtu3b8dbb72FEydOoGnTpjrbf/jwId5880107NgRYWFhSE5OLvP9k7C3oCIiIiLx2T6Y/7xB/R/LZ9dh+2B+iT24Jj4+Hmq1GnXr1jW4zokTJ3D58mWcP38e7u55zfL69evRokULREZGomvXrjrvWbNmDYYNG4aAgAAAgJeXFy5cuIDVq1drNamDBg3CmDFjtN77sslJtra2mt9/8cUXGDlypGYbkydPRlRUFOLinj+Vbc2aNZg4cSKGDh0KAJg1axZOnTqFNWvWYN26dTrb37lzJ548eYLPPvsMdnZ2aNiwIaZMmYLAwMBCc4mMTSoRERG9Motn+u9dbvEspcQ+U23oiQwvuHr1KlxdXTUNKgDUrl0brq6uuHLlit4m9erVq5oJ3Pnat2+Pw4cPa9VatGih8946deoYmR74+++/dZrcVq1aaZrUzMxMJCcno127djpZfvjhB73bvHr1Kho1aqR1ZPm1114zOpOI2KQSERHRK1NZugJP9dWrldhnenp6QpIk/P333wbXKey+6oXdb13fsoK1ihUr6qxTlNP9L8tQGEPvM6ZxL2vYpBIREdEry7YPgeXTGK1T/iX94BpHR0f06NED4eHhCAwM1LkuValUon79+khKSkJCQoLmaOqNGzeQnJyM+vXr691uvXr1cObMGbz11lua2unTpw2u/6KinO6vW7cufvvtN4wePVpT++233zS/r1SpElxdXXHmzBn4+PhoZalXr57e7devXx9bt27Fw4cPNU302bNnX5pbZGxSiYiI6JXlP7jG9sF8WDxLgcqyGrLtQ0r8wTXLly9Hr1690K1bN8yaNQuNGjWCWq1GVFQUVq1ahUuXLqFx48YICAjAkiVLoFarMX36dDRr1gxdunTRu80PPvgA77zzDpo3b47u3bvj6NGj2LlzJ77++uuX5inK6f7x48fj/fffR4sWLdChQwccPHgQMTExUCgUWlkWLVoET09PNG/eHNu3b8fp06dx4sQJvdscMmQIPvnkE0ycOBHTp09HSkoKVqxYYXQmEbFJJSIiomJRW7mX2CQpQ2rXro3IyEisWLECc+bMQXJyMpycnNC4cWOsWrUKkiRhy5YtmDFjBvr27QsA8PHxwdKlSw2eMu/bty+WLl2K0NBQzJw5E7Vq1cKKFSu0Jk2Zgp+fH27cuIG5c+fi8ePH6Nu3L95991189913mnXGjx+PrKwszJkzB3fv3oW3tzc2b96sd2Y/ANjZ2WH79u2YPHkyfHx84O3tjf/85z8YMWKESbOXJmGeOEXyMvenrhQXx694OH6vjmNXPOY+fmX9iVP/JKNGjUJubi62b98ud5RSJewTp4iIiIjMzaNHj7Bhwwa8/vrrsLKywv79+/Hdd99h8+bNckcTCptUIiIiolIkSRKOHj2KlStXIjs7G3Xq1MHatWvRr18/uaMJhU0qERERUSkqX748IiIi5I4hPAu5AxARERERFcQmlYiIiIiEwyaViIjIjP0Tn1REZcPLvntsUomIiMxUxYoVoVQq2ahSqVOr1VAqlXofMZuPE6eIiIjMlJWVFezt7ZGZmSl3FDJD9vb2sLIy3IqySSUiIjJjVlZWvKE/CYmn+4mIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4nN1PRKRHQkIm5s+PQXLyI7i6VkBISGu4u1eSO5ZGfr74+PuoUydRuHxERMXFJpWIqICEhEwMHHgY168/v3dkTMw97NvnK0QjWDDfuXMZQuUjIjIFnu4nIipg/vwYrQYVAK5fzztyKQLR8xERmQKbVCKiApKTH+mtp6Tor5c20fMREZkCm1QiogJcXSvorVerpr9e2kTPR0RkCmxSiYgKCAlpDQ8P7Ws7PTwqISSktUyJtImej4jIFDhxioioAHf3Sti3zxfz58cgJeURqlUTa3b/i/ni41NRp46zUPmIiEyBTSoRkR7u7pUQHt5d7hgG5eeLjY2Ft7e33HGIiEyOp/uJiIiISDhsUomIiIhIOK/UpN66dQsXLlxAVlaWqfMQERERERWtST148CBatmyJpk2bonv37jh37hwAIDU1FR06dMCBAwdKJCQRERERmRejm9QjR45gzJgxqFy5MmbMmAG1Wq1Z5uzsjJo1a+Lbb78tkZBEREREZF6MblKXLl2Ktm3b4ocffoC/v7/O8jZt2uDSpUsmDUdERERE5snoJvXPP//E4MGDDS53cXHB/fv3TRKKiIiIiMyb0U2qtbU1cnJyDC5PTExEpUq8kTQRERERFZ/RTWq7du2wd+9evcsyMzOxZcsWdO7c2WTBiIiIiMh8Gd2kBgcH448//sDAgQNx+PBhAMDFixfx5ZdfwsfHB5mZmZg+fXqJBSUiIiIi82F0k9qiRQvs2rULt2/fxsSJEwEAs2fPxpQpU2BpaYldu3ahXr16JRaUiIiIiMyHVVFW7tSpE86ePYtLly7h2rVrUKlU8PDwQPPmzSFJUkllJCIiIiIzU6QmNV+TJk3QpEkTU2chIiIiIgJQhNP9jo6OqFu3LqKjo/Uu37FjB5ycnEwWjIiIiIjMV5Eei5qTk4OBAwciLCyspPIQERERERWtSV24cCFGjhyJjz76CAEBAcjOzi6pXERERERkxorUpFpbW2P16tVYuXIlIiIi0KtXLyQmJpZUNiIiIiIyU0VqUvONHTsW+/fvR0pKCrp27YrIyEhT5yIiIiIiM/ZKTSoAtG3bFidOnICHhwf8/Pzw9ddfmzIXEREREZmxV25SAcDV1RXfffcdRowYgZMnT5oqExERERGZOaPvk/r777+jcuXKOnVra2uEhoaif//+uHfvnknDEREREZF5MrpJdXNzK3T5v/71r2KHISIiIiICCmlS82/a37FjR63XL5O/PhERERHRqzLYpPbt2xeSJCElJQXW1taa14ao1WpIkoS0tDSThXv27BkWLVqEHTt24M6dO3BxccGbb76J4OBgWFm90hNdiYiIiKgMMNjpHThwAEDeNacvvi5Nn376KdavX4+wsDA0bNgQf/zxB4KCgmBtbY3p06eXeh4qfed++RUZsbPg7JCO1AxHOHgvQKu2r8kdS2P37jh88EEUsrNzYWt7EqGhneHn5yV3LI3vD0ZCfWcuXJwzcCfVAZLLHPTu6yN3rDJh2rSTCA//S/Pa378Bli3rJGMibaJ/90QXHZ2EoKBIpKU9hpNTDMLCfNCxY3W5YxHRCySlUqmWO4Qhw4YNg6OjI7744gtNbfz48UhPT8f27dtlTPbPExsbC29vb7ljaDn3y69wwwh4uaVqanE3nXETW4VoVHfvjsO4ccd16hs2dBOiWfj+YCRaVR4LL/fnZzfiEpxw7v5G4RpV0b5/BRvUfKI0qqJ/90QXHZ2EAQO+Q27u8x9/VlYSIiLeYKNKJJBi3YLq9u3bOHfuHJRKpYniaGvXrh1OnjyJv//+GwBw5coVREVFcZKWmciInaXVoAKAl1sqMmJnyZRI2wcfRBWpXtrUd+ZqNagA4OWeBvWduTIlKjv0NaiF1Uub6N890QUFRWo1qACQm6tGUBAfTEMkkkIv7IyJicFPP/2Ed999F1WqVNHU79y5g3HjxuHUqVMAAEtLS0yYMAFz55r2h9+kSZOQlZWFtm3bwtLSErm5uZg6dSree+89g++JjY01aQZzItrYOTmk669XShcia3Z2rsG6CPlcnDP01qs6ZwiRryARM+kjQk7Rv3uiS0t7bLAu0viJdHaBSA6FNqkbNmxAVFQUZsyYoVV///33ER0djQ4dOqBly5Y4ceIEQkNDUb9+fYwYMcJk4fbs2YNt27Zh/fr1qF+/Pi5duoTg4GC4ublhzJgxet/Dv9SvRrTTrQBw7BdHvfW0TEc0FyCrre1JPHqk2yzY2loJMZaHf3bQW7+b6oBWAuR7kXjfvxMGl4iQU/TvnuicnGKQlZWlp16e40ckkEJP98fExKBPnz5atevXr+Onn35C9+7dcejQIXzyySc4duwYGjZsaPJHo86ePRsTJ06En58fGjVqhOHDh+P999/HqlWrTPo5JCYH7wWIu+msVYu76QwH7wUyJdIWGtq5SPXSJrnMQVyCk1YtLsEJksscmRKVHf7+DYpUL22if/dEFxbmAysr7bvVWFlJCAsT61ptInNXaJN6584dnX9VHjlyBJIk4Z133tHUypUrhyFDhuDPP/80abhHjx7B0tJSq2ZpaQmVSmXSzyExtWr7Gm5iK/b+1AY/x3hh709thJk0BQB+fl7YsKEbKlSwgoUFUKGClVATV3r39cG5+xux7buWOP6LJ7Z911LISVMiWrask05DKsqkKUD8757oOnasjoiIN+DmZgc7O0u4udlx0hSRgF56s1G1Wvvi8l9//RWA7k37q1SpgseP9V/n86p69+6NTz/9FO7u7qhfvz4uXryIzz77DMOHDzfp55C4WrV9DWj7o9wxDPLz84Kfn5eAp6vz5DWkx+SOUSYtW9ZJmKZUH9G/e6Lr2LE6Ll4cwfEjElihR1I9PDxw5swZzevc3FxERUWhbt26cHLSPo2YmpqKypUrmzTc0qVL0b9/f0yZMgVt27ZFSEgI3n77bXz88ccm/RwiIiIiEkuhR1JHjBiBkJAQeHt7o0OHDti1axdSU1Mxfvx4nXWjo6Ph5WXaU0329vZYvHgxFi9ebNLtEhEREZHYCm1Sx40bh+PHj2PJkiWQJAlqtRqdO3fG+++/r7VeYmIijh07htmzZ5doWCIiIiIyD4U2qeXKlcP27dtx/vx5XL9+HW5ubmjdurXOek+fPsX69et1rlMlIiIiInoVL504BQAtWrRAixYtDC6vU6cO6tSpY7JQRERERGTeivVYVCIiIiKiksAmlYiIiIiEwyaViIiIiITDJpWIiIiIhMMmlYiIiIiEwyaViIiIiIRj8BZUS5YsKfLGJEnC9OnTixWIiIiIiMhgk/oqjyJlk0pEREREpmCwSU1PTy/NHEREREREGrwmlYiIiIiEwyaViIiIiIRj8HR/v379irwxSZKwf//+YgUiIiIiIjLYpKpUKkiSVKSNqdXqYgciIiIiIjLYpB46dKg0cxARERERafCaVCIiIiISTpGa1GfPnmHHjh2YOHEihg0bhsuXLwMAlEol9u7di5SUlBIJSURERETmxegmNSMjAz179kRgYCAiIiLw448/IjU1FQBgb2+PWbNmYd26dSUWlIiIiIjMh9FN6ty5c3HlyhXs3LkTFy5c0JokZWlpiX79+uHHH38skZBEREREZF6MblIPHTqEgIAAvP7663pn/Xt6eiIxMdGk4YiIiIjIPBmc3V+QUqmEh4eHweVqtRpPnjwxSSiifEkJl3H/r5moYHMfj3Iqo3KDRaju3ljuWBrnfvkVGbGz4OSQjmO/OMLBewFatX1N7lgaCQmZmD8/BsnJj+DqWgEhIa3h7l5J7lhlQnR0EoKCIqFU5kChsEFYmA86dqwudyyN/H0bH38fdeokCrdvRf/uiT5+RFSEJtXNzQ1//vmnweXR0dHw8vIySSgiIK9BLX9/EDo3u6ep3UgahCTsFaJRPffLr3DDCHj1SNXU4m6OwLlftgrRqCYkZGLgwMO4fj1TU4uJuYd9+3z5w/gloqOTMGDAd8jNzbusKTPzKQYM+A4REW8I0agW3LfnzmUItW9F/+6JPn5ElMfo0/1Dhw7F5s2bER0dranln/Zfu3YtDh48iJEjR5o+IZmt+3/NRO3q97Rqtavfw/2/ZsqUSFtG7Cx4uaVq1bzcUpERO0umRNrmz4/RahIA4Pr1vKNHVLigoEhNg5ovN1eNoKBImRJpE33fMh8RmYLRR1I//PBDxMTEoH///vDy8oIkSQgODkZaWhru3LmDPn36IDAwsCSzkpmpYHPfQD1Vb720OTukF6le2pKTH+mtp6Tor9NzSmWO3npGhv56aRN93zIfEZmC0U1quXLlsGPHDuzcuRP79u2DJEnIzc1Fs2bNMHjwYLz55ptFfowqUWEe5VQ2UHcu5ST6pWY4Fqle2lxdK+itV6umv07PKRQ2yMx8qlN3cLCRIY0u0fct8xGRKUhKpVL98tXony42Nhbe3t5yx9CSf03qi6f8byRVwePKgl2T6vbiNanOuAlxr0n18Kgk5HV3on3/Cl6TCgBWVpKw16QCYu1b5iMiU3hpk7p7927Y2dmhV69eBtc5cuQIHj58iMGDB5s8IJUO0ZqEfM9n96fiUY6zuLP7K6UjLVPc2f0pKY9QrZp4M6zzifj9y5/dn5GRAwcHkWf3p6JOHWfh9q3o3z3Rx4+IXtKkHjx4EGPGjMGOHTvw+uuvG9zITz/9hKFDh2Lbtm3o2bNniQSlkiVik1CWcPyKh+P36jh2xcPxIxJXobP7t2zZgvbt2xfaoAJAjx490LFjR2zatMmk4YiIiIjIPBXapJ47d67Q0/wv+te//oWYGN6+g4iIiIiKr9AmValUwtnZuJnUzs7OSE8X49Y7RERERFS2FdqkOjg4IDk52agNpaSkwMHBwSShiIiIiMi8FdqktmzZEhEREUZtaN++fWjZsqVJQhERERGReSu0SX3nnXdw+fJlBAcHQ6VS6V1HrVZj5syZ+OOPPzB27NgSCUlERERE5qXQJ075+vpi1KhRWLt2LU6cOIEhQ4agYcOGsLOzQ1ZWFv7880/s2rULV69exVtvvYXevXuXVm4iIiIi+gd76WNR16xZg7p16+LTTz/FggULtB59qlaroVAoMG/ePHzwwQclGpSIiIiIzMdLm1QA+L//+z8EBATgzJkzuHr1Kh48eAB7e3vUq1cP7dq1g62tbUnnJCIiIiIzYlSTCgC2trbo2rUrunbtWoJxiIiIiIheMnGKiIiIiEgObFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOAZvQbVkyZIib0ySJEyfPr1YgYiIiIiIDDapixcvLvLG2KQSERERkSkYbFLT09NLMwcRERERkQavSSUiIiIi4bBJJSIiIiLhGDzdr8+VK1fwxRdf4MKFC8jIyIBKpdJaLkkSLly4YMp8RERERGSGjD6S+ssvv6Bbt244dOgQXFxccOPGDdSuXRuurq5ITExExYoV0aFDh5LMSkRERERmwugmdf78+ahevTrOnj2Lzz//HAAwefJkfP/99zh8+DBu376NIUOGmDxgSkoKxo8fD09PT7i4uKBt27Y4efKkyT/HXEVHJ6Fp063o1i0KTZtuRXR0ktyRtHzxxSU4O6+HQhEOZ+f1+OKLS3JH0jJt2kkoFOFo0+YEFIpwTJsm1ndT9PFLSMiEv/8xjB9/Hv7+x5CQkCl3JI2xo9fiwLpuOLevFQ6s64axo9fKHUmL6N+9/H3bt+9B4fYtACxYcBaOjnnj5+gYjgULzsodiYgKMPp0//nz5zFt2jQoFArNzP/80/1t27bF22+/jQULFqB79+4mC6dUKtGrVy+0a9cOO3bsgLOzMxISElClShWTfYY5i45OwoAB3yE3Vw0AyMrKwoAB3yEi4g107Fhd5nR5DVZw8BnN62fP1JrX48c3kSuWxrRpJxEe/pdWLf/1smWd5IikRfTxS0jIxMCBh3H9el7zcu5cBmJi7mHfPl+4u1eSNdvY0WuxdOISeLmnaWrtmiZg7Ghg4zeBMibLI/p3r+C+BSDMvgXyGtRlyy5oXqvV0LyeNauNPKGISIfRR1IlSYKDgwMAoEKFCgCAtLTn/wP38vLCX3/9pfe9r+q///0vqlWrhrVr16JVq1aoXbs2fHx8UK9ePZN+jrkKCorUNKj5cnPVCAqKlCmRtlmzfilSvbQVbBJeVi9too/f/PkxWk0MAFy/non582NkSvTc4C7btBpUAPByT8PgLttkSqRN9O+eyPsWAJYvv1CkOhHJw+gjqW5uboiPjwcA2NjYwN3dHcePH4efnx8A4NSpU3BycjJpuEOHDqFHjx4YO3YsoqKiUK1aNYwZMwb+/v6QJEnve2JjY02a4Z8sLe2xwboI4/jsmdpgXYR8hREhn+jjFx9/30A9VfZ81avqPzVdvUqm7NleRoR8Iu9bIO/IqaG6CPnyeXt7yx2BSFZGN6ndunVDREQE5s6dC0mS8Pbbb2PevHm4efMm1Go1Tp48iUmTJpk03I0bN7BhwwZMmDABkyZNwqVLlzBjxgwAQEBAgN738C+18ZycYpCVlaWnXl6IcbS0jNTbaFlaSkLkA04YXCJCPtHHr06dRJw7l6Gn7ix7vgPH9Z+STrpXCa0EGDvRv3si71sAkKQTehtVSRJj/Igoj9Gn+6dOnYpNmzYhNzcXADBp0iR8/PHHSE9Px4MHDxAcHIyPPvrIpOFUKhWaNWuGOXPmoFmzZhg9ejQCAwOxfv16k36OuQoL84GVlfYRaSsrCWFhPjIl0rZgQdsi1Uubv3+DItVLm+jjFxLSGh4e2s2gh0clhIS0linRc3t+Ho64BO0zQ3EJTtjz83CZEmkT/bsn8r4FgKlTmxepTkTykJRKpYETH/Jr3LgxunXrhtDQUE1t27ZtmDx5MpKSxJqFXlZFRychKCgSaWmP4eRUHmFhPkJMmsr3xReXMGvWL3j2TA1LSwkLFrQVYtJPvoITWPz9GwgxcSWf6OOXkJB3nWJ8fCrq1HFGSEhrISbWAHmTpwZ32YbqVTKRdK8S9vw8XIhJU/lE/+7l79uUlEeoVq2CUPsWyJs8tXz5BajVeUdQp05tzklTRIIRukl97733cPv2bRw+fFhTmz9/Pg4cOIBffhFj8sc/RWxsLE9zFQPHr3g4fq+OY1c8HD8icRm8JnXJkiWQJAlTp06FhYUFlixZ8tKNSZKE6dOnmyzchAkT0LNnTyxfvhyDBw/GxYsXsW7dOnz88ccm+wwiIiIiEo/BI6mOjo6QJAkpKSmwtraGo6PjyzcmSVq3pTKFI0eOYN68eYiLi0PNmjXh7++PwMBAg7P76dXwaELxcPyKh+P36jh2xcPxIxKXwSOp+TfsN/S6tPTq1Qu9evWS5bOJiIiISB5Gz+4nIiIiIiotbFKJiIiISDgGT/f369evyBuTJAn79+8vViAiIiIiIoNNqkqlKvLkJLWhZ80RERERERWBwSb10KFDpZmDiIiIiEiD16QSERERkXCK1KQ+e/YMO3bswMSJEzFs2DBcvnwZAKBUKrF3716kpKSUSEgiIiIiMi9GN6kZGRno2bMnAgMDERERgR9//BGpqakAAHt7e8yaNQvr1q0rsaBEREREZD6MblLnzp2LK1euYOfOnbhw4YLWJClLS0v069cPP/74Y4mEJCIiIiLzYnSTeujQIQQEBOD111/XO+vf09MTiYmJJg1HRERERObJ6CZVqVTCw8PD4HK1Wo0nT56YJBQRERERmTejm1Q3Nzf8+eefBpdHR0fDy8vLJKGIiIiIyLwZ3aQOHToUmzdvRnR0tKaWf9p/7dq1OHjwIEaOHGn6hERERERkdgzezL+gDz/8EDExMejfvz+8vLwgSRKCg4ORlpaGO3fuoE+fPggMDCzJrERERERkJoxuUsuVK4cdO3Zg586d2LdvHyRJQm5uLpo1a4bBgwfjzTffLPJjVImIiIiI9DG6Sc03dOhQDB06tCSyEBEREREB4GNRiYiIiEhARTqSeuLECWzatAk3btxAenq61g39gbyJVBcuXDBlPiIiIiIyQ0Y3qWFhYZg1axYqV66M1q1bo0GDBiWZi4iIiIjMmNFN6meffYaOHTti9+7dsLa2LslMRERERGTmjL4mNTU1FYMHD2aDSkREREQlzugmtXnz5rh582ZJZvlHupvwA7L/8IYUVx3Zf3jjbsIPckcqU37+YTvSYzygulIN6TEe+PmH7XJH0vL9wUgc3tAdD/4YjsMbuuP7g5FyR9KyYMFZODqGQ6EIh6NjOBYsOCt3JC0JCZnw9z+G8ePPw9//GBISMuWOpNG+/TYoFOGaX+3bb5M7kpb8fdumzQkh9210dBKaNt0KN7ev0LTpVkRHJ8kdSUt+vm7dooTMR0SApFQq1S9fDfjtt98wYsQIhIeHo0uXLiWd6x/hbsIPqC0NR7lyKk3t6VML3FBvQ1X3njIm0xUbGwtvb2+5Y2j5+Yft6FU/CNYvjN+TpxY4ciUMXXoOkzFZnu8PRqJV5bHwck/T1OISnHDu/kb07usjY7I8CxacxbJlF3Tq06Y1x6xZbUo/UAEJCZkYOPAwrl9/3ph6eFTCvn2+cHevJGOyvAb1r78e6NQbNLDH6dPDZUikTfR9Gx2dhAEDvkNu7vMfL1ZWEiIi3kDHjtVlTJZH9HxElMdgk6rvXqg3btzAtWvX4OnpiVq1asHS0lJ7Y5KEHTt2lEzSMij7D2+4ON3Tqd9JqwLbRrEyJDJMxCY1PcYDtWuk69Rv3HaEY+vrMiTSdnhDdwx/4zed+rbvWsJ33DEZEmlzdAyHWs/fbkkC0tP9Sz9QAf7+x7Bz5zWd+tChnggP7y5DoucUinCDy5RK+cdO9H3btOlW3LyZpVN3c7PDxYsjZEikTfR8RJTH4MSpK1eu6H2CVM2aNZGTk4O4uLgSDfZPUN7mocG6UYevzZyD3eMi1Uubi3NGkeqlTV8TU1i9tCUnP9JbT0nRX6fnRN+3SmWO3npGhv56aRM9HxHlMdikXrp0qTRz/CM9zqmIShV1f+A+zqkIWxnylDUZWeXh6JCtvy5DnoLupDoUqV7aJEl/0yLK04tdXSvorVerpr9Oz4m+bxUKG2RmPtWpOzjYyJBGl+j5iCiP0ROnoqOjcf/+fYPLU1NTER0dbZJQ/xSZdp/h6VPtIX761AKZdp/JlKhsuZS2GE8KjN+Tpxa4lLZYpkTaJJc5iEtw0qrFJThBcpkjUyJtU6c2L1K9tIWEtIaHh/a1px4elRAS0lqmRM81aGBfpHppE33fhoX5wMpKu2O2spIQFib/tdqA+PmIKI/RE6ecnJywdu1avdeqAsCePXvw3nvvIS0tTe9yc3U34QdUynof5W0e4nFORWTafSbcpClAzGtSgbzJU02cguFg9xgZWeVxKW2xEJOm8n1/MBLqO3NR1TkDd1MdILnMEWLSVL4FC85i+fILUKvzjrJNnSrGxJp8CQmZmD8/BvHxqahTxxkhIa1lnzSVr+DkKVEmTeUTfd9GRychKCgSGRk5cHCwQViYj1CTkvLzpaU9hpNTeeHyEVERmlRHR0esW7fOYJO6bds2TJw4sdCjrSQuUZvUsoLjVzwcv1fHsSsejh+RuAp94lRmZiYyMp5PAklLS0NiYqLOekqlErt374arq6vpExIRERGR2Sm0Sf3888+xdOlSAHm3l5o5cyZmzpypd121Wo2PP/7Y9AmJiIiIyOwU2qR27doVtra2UKvVmDdvHgYPHowmTZporSNJEipUqIAWLVqgdWv5JzwQERERUdlXaJParl07tGvXDgCQk5ODfv36oVGjRqUSjIiIiIjMV6FN6ouCg4NLMgcRERERkYbBJnXr1q0AgOHDh0OSJM3rlxkxgo+UIyIiIqLiMdikTpgwAZIkwc/PD9bW1pgwYcJLNyZJEptUIiIiIio2g03q77//DgCwtrbWek1EREREVNIMNqlubm6FviYiIiIiKilGT5x60eXLlzU39a9VqxYaNWoESZJe8i4iIiIiIuMUqUndvXs35syZg6SkJK169erVMWfOHIOPTCUiIiIiKgqjm9QtW7Zg4sSJ8Pb2xty5c+Hl5QW1Wo1r165h8+bNCAwMxJMnTzBq1KiSzEtEREREZsDoJnXlypVo1aoVDh48CFtbW61l/v7+eOONN7By5Uo2qURERERUbBbGrnj79m0MHTpUp0EFAFtbWwwbNkznMgAiIiIioldhdJNav359JCcnG1yelJSEevXqmSQUEREREZk3o5vUefPmYdOmTdi7d6/Ost27d2Pz5s345JNPTBqOiIiIiMyT0dekhoaGwtnZGePGjUNwcDA8PDwgSRLi4+Nx7949eHp64r///S/++9//at4jSRJ27NhRIsGJiIiI6J/L6Cb1ypUrkCQJNWvWBADN9ac2NjaoWbMmcnJycPXqVa338N6pRERERPQqjG5SL126VJI5iIiIiIg0jL4mlYiIiIiotBTapK5fvx7x8fGa1yqVCleuXMHjx4911j1//jymT59u+oREREREZHYKbVKnT5+Oc+fOaV4rlUp06NABv/76q866sbGxWL9+vekTEhEREZHZKbRJVavVRtWIiIiIiEypTF2TumLFCigUCkybNk3uKERERERUgspMk3r27Fls2rQJjRo1kjtKkUi5CSif7o+K9/uifLo/pNwEuSNpsciOht2dpmheoRvs7jSFRXa03JG0fLNuPVLPekB1pRpSz3rgm3ViXVLy+af7cWBdN2T+MRwH1nXD55/ulzuSlmnTTkKhCNf8mjbtpNyRtERHJ6Fp063o1i0KTZtuRXS0OI9W7u+7GgfWdcO5fa1wYF039PddLXckLQsWnIWjYzjatDkBR8dwLFhwVu5IWvL3rZvbV8LtWwDYvTsO1atvRNu2J1C9+kbs3h0ndyQiKsDoW1DJKSMjA/7+/ggNDcXSpUvljmM0KTcBFdMGwvLZ9bzCU8DyaQweOu2D2spd3nD4X4OaPgAScvP+uaLKgl36AGQ5RkBl21HuePhm3Xr4954O63IqAICjQzb8XaYjfB0wOuA9mdPlNahD202Cl3uaphaXMAmffwpMmNRfvmD/M23aSYSH/6VVy3+9bFknOSJpiY5OwoAB3yE3N+8SoqysLAwY8B0iIt5Ax47VZc3W33c1NsxZrbVv2zVNQH9fYP/hf8uYLM+CBWexbNkFzWu1GprXs2a1kSfUCwru28zMp8LsWyCvQR037rjm9aNHuZrXfn5ecsUiogJeeiQ1JiYGe/fuxd69e3Hw4EFIkoTo6GhNLf/X2bMl96/4SZMmYcCAAfDx8SmxzygJtg/mP29Q/8fy2XXYPpgvUyJtFTKC8hrUF0jIRYWMIJkSafNtsUDToOazLqeCb4sFMiXSVqvCKq0mBgC83NNQq8IqmRJpK9igvqxe2oKCIjVNTL7cXDWCgiJlSvSc/6B9evet/6B98gQqYPnyC0WqlzaR9y0AfPBBVJHqRCSPlx5JXbduHdatW6dVW7Zsmd51S+IJU5s2bUJ8fDzWrl1r1PqxsbEmz/Cq6trGw1rPCGdnxSP2vvw5m1dI0/vPFHVumhDj6Gmve6szAFDYPxYiX/WqmfrrVTKFyFcYEfKlpenfv2lp8u9f0fetofmrajX3rTGys3MN1kXIl8/b21vuCESyKrRJPXDgQGnl0Cs2Nhbz5s3D4cOHYW1tbdR7RPpLbZteB8g+p1u3qwPvWvLnlO44Aaos3bqVkxDjmHq2PBwdsnXqygfl4d1G/nwHjlfSW0+6VwmtBBg/4ITBJSLsXyenGGRl6X7/nJzKy55P9H0rSSf0NqqSxH1rDFvbk3j0SLdRtbW1EiIfEeUp9HR/p06divzLlH799Vekpqaiffv2cHZ2hrOzM6Kjo7F+/Xo4OzsjJyfHpJ9natn2IXhm6aFVe2bpgWz7EJkSaXvkEAZ1gX+nqGGFRw5hMiXSdvj8LDx5qv0VffLUAofPz5IpkbbERx8iLsFJqxaX4ITERx/KlEibv3+DItVLW1iYD6ystM++WFlJCAuT/7Ke8L0D9e7b8L0D5QlUwNSpzYtUL20i71sACA3tXKQ6EclDUiqVwt74VKlUIilJe0bo+++/D09PT0yePBkNGjQokUsMTEnKTYDtg/mweJYClWU1ZNuHCDFpKp9FdjQqZARBnZsGycoJjxzChJg0le+bdevh22IBFPaPoXxQHofPzxJi0lS+zz/dj1oVVqF6lUwk3auExEcfCjFpKl/ByVP+/g2EmDSVLzo6CUFBkUhLewwnp/IIC/MRYmINkDd5yn/QPs2+Dd87UIhJU/kWLDiL5csvQK3OO4I6dWpzISZN5cvftxkZOXBwsBFq3wJ5k6c++CAK2dm5sLW1QmhoZ06aIhKM0E2qPn369EHDhg0NXhdLryY2NpanuYqB41c8HL9Xx7ErHo4fkbjKzH1SiYiIiMh8lIn7pL7o0KFDckcgIiIiohLGI6lEREREJBw2qUREREQknCI1qZmZmVi+fDn69++PDh06ICYmBgCQlpaG1atX49q1ayUSkoiIiIjMi9HXpCYlJeGNN97A7du34enpib///hsPHz4EADg5OWHz5s1ISkrCkiVLSiwsEREREZkHo5vU//znP8jMzERkZCRcXFzg5aV9P7k+ffrghx9+MHlAIiIiIjI/Rp/uP3r0KAIDA9GwYUO9N9CvXbu2zo33iYiIiIhehdFN6qNHj+Di4lLocpVKZZJQRERERGTejG5SPT09ce7cOYPLjx49ioYNG5okFBERERGZN6Ob1Lfffhvbtm3Dtm3bNEdMJUnCw4cP8fHHH+Pnn3/GuHHjSiwoEREREZkPoydOBQQE4K+//kJQUBDs7e0BAO+++y6USiWePXuGwMBADBs2rMSCEhEREZH5KNJjUVetWoXhw4dj7969iI+Ph0qlgoeHBwYPHoz27duXVEYiIiIiMjNFalIBoG3btmjbtm1JZCEiIiIiAsDHohIRERGRgAweSe3Xr1+RNyZJEvbv31+sQEREREREBptUlUql96b9hVGr1cUORERERERksEk9dOhQaeYgIiIiItLgNalEREREJByjZ/cnJiYWulySJNja2sLZ2bnIlwkQEREREb3I6Ca1adOmRjWftra26NixI6ZPn442bdoUKxwRERERmSejm9TQ0FCsW7cOiYmJGDJkCLy8vKBWq3Ht2jXs2rUL7u7uGDlyJK5du4YdO3agb9++2LdvH2/yT0RERERFZnSTmpaWhsePH+O3336Do6Oj1rLg4GD06tULOTk5WLJkCaZNmwYfHx8sXrwYERERJg9NRERERP9sRk+cCg8Px5gxY3QaVABwdnbGmDFjEB4eDgCoXLkyRo8ejfPnz5suKRERERGZDaOb1Hv37iE3N9fg8tzcXNy9e1fzunr16oWuby5sknvDPlmBSskK2CcrYJPcW+5IWmySu8I+WYFWFdv8L19XuSNp2bhiBOxuKVApSQG7WwpsXDFC7khaFs/bhQPruiHzj+E4sK4bFs/bJXckLbt3x6F69Y1wdg5H9eobsXt3nNyRtHx/MBKHN3THgz+G4/CG7vj+YKTckTRatdoChSJc86tVqy1yR9ISHZ2Epk23olu3KDRtuhXR0UlyR9KSn8/N7Suh84k6fkQESEql0qg78Pfo0QN37tzBkSNHUKNGDa1lt27dQu/evVGtWjUcPXoUABASEoKDBw/iwoULJg9dVtgk94YNzuDF6WZqADlohxzX7+WKpWGT3BU2uKAnX3PkuJ6QKdVzG1eMwL9HHMaL8/XUamD1Vl+MnbJVvmD/s3jeLozrOR1e7mmaWlyCEzb8sBTBs4fImCzP7t1xGDfuuE59w4Zu8PPzkiGRtu8PRqJV5bE643fu/kb07usjY7K8BvXatUc6dU/PCjh3bpQMibRFRydhwIDvkJv7/H/fVlYSIiLeQMeO1WVMlof5iMgUjG5ST58+DT8/P6jVavj6+qJOnToAgPj4eBw+fBhqtRp79+5F+/btkZ2djaZNm6JXr14IDQ0t0T+AyOyTFXoPVasAPHBVlnIaXaLns7ulgKWlbv3ZMyCrprLU8xR0YF03jO6ne0nLNwdaoF+AbnNY2qpX34hHj3TPZlSoYIWkpLEyJNJ2eEN3DH/jN536tu9awnfcMRkSPadQhBtcplT6l2IS/Zo23YqbN7N06m5udrh4Uf6zDcxHRKZg9MSp9u3b48iRI1i4cCG+//57PH78GABQvnx5dOvWDTNnzkSTJk0A5N2G6u+//y6ZxGWIoRt2iXIXWdHzWRi4GMVQvbRVr5qpv15Ff7205eTov9zGUL20uThnFKlOzymVOXrrGRn666WN+YjIFIxuUgGgSZMm2Lp1K1QqFe7duwcAqFKlCixE6RoEo4b+hs+oQ9elQPR8KhX0HklVqUo/iz5Jdyvpr9+rhFalnEUfGxsrvUdSbWyK9Ne+xNxJdShSnZ5TKGyQmflUp+7gYCNDGl3MR0Sm8ErdpYWFBVxcXODi4sIGtRBP0E6n4VP/ry6CJ2huIF9zGdLoCt3uC3WBgGp1Xl0Ef6S8j7gEJ61aXIIT/kh5X6ZE2kJDOxepXtoklzl6x09ymSNTouc8PSsUqV7awsJ8YGWl/U9MKysJYWHyXsubj/mIyBSMviYVAJRKJXbv3o0bN24gPT0d6gIdhCRJWLNmjclDlmU2yb1h/b/JU/kNqgiTpvLZJHeFNS5AUgNqKa9BFWHSVL6NK0bgg2GHYWGRdwQ1dLsYk6byLZ63C42qfYbqVTKRdK8S/kh5X4hJU/l2747DBx9EIScnFzY2VggN7SzEpKl83x+MhPrOXFR1zsDdVAdILnNknzSVr+DkKVEmTeWLjk5CUFAk0tIew8mpPMLCfISa9JOfLyMjBw4ONsLmE3X8iKgITWpkZCTeeustPHjwAPb29lAoFLobkyT8/vvvps5IpSA2Nhbe3t5yxyizOH7Fw/F7dRy74uH4EYnL6IvTPvroIzg6OuLQoUOaCVJERERERCXB6AtK4+LiEBQUxAaViIiIiEqc0U2qu7s7srOzSzILERERERGAIjSpkydPxsaNG5Genl6SeYiIiIiIjL8m9c6dO3ByckLLli0xaNAg1KxZE5YFbmIpSRL+7//+z+QhiYiIiMi8GN2k/uc//9H8fuPGjXrXYZNKRERERKZgdJPKW0sRERERUWkxukl1c3MryRxERERERBp8pikRERERCcfgkdS+ffvCwsICe/bsgZWVFfr16/fSjUmShP3795s0IBERERGZH4NNqlqthkql0rxWqVSQJKnQjanVRj1hlYiIiIioUAab1EOHDhX6moiIiIiopPCaVCIiIiISjtGz+wuKiorCjh07kJKSgrp162L8+PGoVauWKbMRERERkZkq9Ejq4sWLUaVKFdy5c0ervmXLFgwYMADffPMNjh49is8//xzdu3fHzZs3SzQsEREREZmHQpvUqKgodO/eHS4uLppaTk4OZs6ciUqVKiEiIgK3bt3Cl19+iaysLKxcubLEAxMRERHRP1+hTWp8fDxat26tVYuMjMSDBw8wceJEdOnSBRUrVsSgQYPw5ptv4sSJEyWZlYiIiIjMRKFNanp6OqpVq6ZVi4qKgiRJ6NWrl1a9efPmSElJMX1CIiIiIjI7hTapVatWRVJSklbt9OnTsLOzQ+PGjbU3ZGEBa2tr0yckIiIiIrNTaJPasmVLfPvtt1AqlQCAy5cv4/z58+jSpYvOjf2vXr2KGjVqlFhQIiIiIjIfhd6Catq0aejevTtatmyJ+vXr4/Lly5AkCf/+97+11lOr1Th48CC6d+9eomGJiIiIyDwUeiS1UaNGiIiIQOvWrXH//n289tpr2LNnD9q0aaO1XlRUFOzs7NC/f/8SDUtERERE5uGlN/Nv164dduzYUeg6Xbp0walTp0wWioiIiIjMm9CPRV25ciW6deuGWrVqwdPTE8OGDcOff/4pdywiIiIiKmFCN6knT57EuHHjcOTIEezfvx9WVlYYOHAg0tPT5Y5mNJsEBexvK1ApKe+/NgkKuSNpsbmel6tVxTZ5+a4r5I6kJT+fZvwEy/fTvpWwiKuKZravwSKuKn7aJ9YDLSK+XgKLuKqokOgIi7iqiPh6idyRtCQkZMLf/xjGjz8Pf/9jSEjIlDuSxs8/bEd6jAdUV6ohPcYDP/+wXe5IRERmRVIqlWq5QxgrKysLbm5u2LJlC3x9feWO81I2CQrYlANevBGCWg3kPAVy3JWy5cpnc10BGxs9+XKAHA+lbLnyiZ7vp30rMei1eTr59v46Gz0GTpYv2P9EfL0Eb/VYpJPv659mYsBbM+QL9j8JCZkYOPAwrl9/3ph6eFTCvn2+cHevJGOyvAa1V/0gWJdTaWpPnlrgyJUwdOk5TMZkumJjY+Ht7S13jDKL40ckLqGPpBaUlZUFlUoFhUIhdxSjWFtpN1hA3mvrl14JXDqsrQ3kE+R2t6Ln+1fjxXrz/avxYnkCFTCo/Qq9+Qa1XyFPoALmz4/RalAB4Pr1TMyfHyNToueaOAVrNagAYF1OhSZOwTIlIiIyP4K0S8YJDg5GkyZN8NprrxlcJzY2thQTFa5VRf11SRIjJ/MVTzPbp3rrtjZP8TvzvVR8/H0D9VTZ96+n3WO99Up2j2XPpo+ImcoSUcePR3jJ3JWZJvWjjz7CmTNn8P3338PS0tLgeiL9pVbf1j0SCOSdchUhJ/MVT3ZcOZSzeqJbzynHfEaoUycR585l6Kk7y54vPaY8HB2ydeqZWeXh3Vr+sXsRT1cXD8ePSFxl4nT/zJkzsXv3buzfvx+1a9eWO47RnuTmNVQvUqvz6iJ48sRAPt2+Rhai5/vxcrDefD9eFuOU8N7TU/Tm23t6ijyBCggJaQ0PD+1rTz08KiEkpLVMiZ67lLYYT55q/+/xyVMLXEoT41IOIiJzIPzEqRkzZmDPnj04ePAg6tWrJ3ecIrNJUGiuTc1vUEWYNJXP5rpCc+1nfgMowqSkfKLn+2nfSvyr8WLY2jxFdk45/Hg5WIhJU/kivl6CQe1XaPLtPT1FiElT+RIS8q5BjY9PRZ06zggJaS37pKl8P/+wHU2cguFg9xgZWeVxKW2xcJOmAB4JLC6OH5G4hG5Sp06diu3bt+Obb75B/fr1NfWKFSvCzs5OxmT/PPwfdfFw/IqH4/fqOHbFw/EjEpfQp/vXr1+PBw8eYMCAAahXr57mV2hoqNzRiIiIiKgECT1xSqlUyh2BiIiIiGQg9JFUIiIiIjJPbFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOFZyB/ins0luBWtcgwRADeAJPJHjek7uWBo2CTVgbfUQrSoC6tvAk9yKyHG/LXcsDZvk3rDGmRfGrx1yXL+XOxaZAYvsaFTICIKkUkJtocAjhzCobDvKHYuIyGzwSGoJskluBRtcgwUACXmDbYNrsEluJXOyPDYJNWBT7iEsLABJAiwsAJtyD2GTUEPuaADyGlQbnCkwfmdgk9xb5mT0T2eRHQ279AGwVN2EBTJhqboJu/QBsMiOljsaEZHZYJNagvKPoL5I+l9dBNZWDyEVCChJeXUR5B9BfZH0vzpRSaqQEQQJuVo1CbmokBEkUyIiIvPDJrUEFWywXlYvbQUb1JfVS5vo40f/XJJKaaCeUbpBiIjMGJvUEqQuYr20qQ0EMVQvbaKPH/1zqS0UBuoOpRuEiMiMsUktQU/gqdNQ5U+eEsGT3Io6DalanVcXwRO0MzB+7eSIQ2bkkUMY1AXmlaphhUcOYTIlIiIyP2xSS1CO6znkwBMq5DVXKgA5As3uz3G/jZynFaFS5TWnKhWQ81Sc2f05rt8jB+0KjB9n91PJU9l2RJZjBJ5ZuEEFBzyzcEOWYwRn9xMRlSLegqqE5TWq4spxv40cALGxsfD29pY7jo68RpWo9KlsOyLL9qLcMYiIzBaPpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDKRJO6fv16NG3aFC4uLvDx8cGpU6fkjkREREREJUj4JnXPnj0IDg7GlClT8PPPP+O1117D0KFDkZiYKHc0IiIiIiohklKpVMsdojA9evRAo0aN8N///ldTa9myJQYMGIA5c+bImIyIiIiISorQR1KfPHmCCxcuoHv37lr17t2745dffpEpFRERERGVNKGb1NTUVDx79gxVqlTRqlepUgV3796VKRURERERlTShm9R8kiRpvVar1To1IiIiIvrnELpJdXZ2hqWlpc5R0/v37+scXSUiIiKifw6hm1Rra2s0b94cx48f16ofP34cbdu2lSkVEREREZU0K7kDvMz777+PwMBAtGrVCm3btsWXX36JlJQUjB07Vu5oRERERFRChD6SCgCDBw/GokWLsGzZMnTu3BlnzpzBjh074ObmplmHN/t/NStXrkS3bt1Qq1YteHp6YtiwYfjzzz/ljlUmrVixAgqFAtOmTZM7SpmRkpKC8ePHw9PTEy4uLmjbti1Onjwpd6wy4dmzZ5g/f77m/3tNmzbF/PnzkZubK3c0IUVHR2P48OFo0KABFAoFtmzZorVcrVZj0aJFqF+/PqpVq4Y+ffrgr7/+kiktEeUTvkkFgPfeew+XLl3C3bt3ERkZiY4dO2qW8Wb/r+7kyZMYN24cjhw5gv3798PKygoDBw5Eenq63NHKlLNnz2LTpk1o1KiR3FHKDKVSiV69ekGtVmPHjh345ZdfsHTpUl5rbqRPP/0U69evx5IlS/Drr79i8eLFCA8Px8qVK+WOJqSHDx+iYcOGWLx4McqXL6+zfPXq1fjss8+wZMkSHDt2DFWqVMGgQYPw4MEDGdISUT7hb+b/MrzZv+lkZWXBzc0NW7Zsga+vr9xxyoSMjAz4+Phg9erVWLp0KRo2bIhly5bJHUt48+bNQ3R0NI4cOSJ3lDJp2LBhcHR0xBdffKGpjR8/Hunp6di+fbuMycRXo0YNLF26FKNGjQKQdxS1fv368Pf3x9SpUwEAjx8/hre3Nz755BNeWkYkozJxJNUQ3uzftLKysqBSqaBQKOSOUmZMmjQJAwYMgI+Pj9xRypRDhw6hVatWGDt2LLy8vNCpUyesW7cOanWZ/jdzqWnXrh1OnjyJv//+GwBw5coVREVF4V//+pfMycqehIQE3LlzR+vnSPny5dGhQwf+HCGSmfATpwrDm/2bVnBwMJo0aYLXXntN7ihlwqZNmxAfH4+1a9fKHaXMuXHjBjZs2IAJEyZg0qRJuHTpEmbMmAEACAgIkDmd+CZNmoSsrCy0bdsWlpaWyM3NxdSpU/Hee+/JHa3MuXPnDgDo/TmSnJwsRyQi+p8y3aTm483+i++jjz7CmTNn8P3338PS0lLuOMKLjY3FvHnzcPjwYVhbW8sdp8xRqVRo0aKF5pKcZs2aIT4+HuvXr2eTaoQ9e/Zg27ZtWL9+PerXr49Lly4hODgYbm5uGDNmjNzxyiT+HCEST5luUnmzf9OYOXMm9uzZgwMHDqB27dpyxykTfv31V6SmpqJ9+/aa2rNnz3Dq1Cl8+eWXSEpKgo2NjYwJxebi4oJ69epp1erWrYtbt27JlKhsmT17NiZOnAg/Pz8AQKNGjZCYmIhVq1axSS0iFxcXAMDdu3dRs2ZNTZ0/R4jkV6avSeXN/otvxowZ2LVrF/bv34+6devKHafM6NOnD06dOoWoqCjNrxYtWsDPzw9RUVE8uvoS7dq1Q1xcnFYtLi4OtWrVkilR2fLo0SOdMx6WlpZQqVQyJSq73N3d4eLiovVzJDs7G6dPn+bPESKZlekjqQBv9l8cU6dOxfbt2/HNN99AoVBors2qWLEi7OzsZE4nNoVCoTPBrEKFCnB0dETDhg3lCVWGTJgwAT179sTy5csxePBgXLx4EevWrcPHH38sd7QyoXfv3vj000/h7u6O+vXr4+LFi/jss88wfPhwuaMJKSsrC/Hx8QDyLjW5desWLl68CEdHR9SqVQtBQUFYsWIFvL294eXlheXLl6NixYoYMmSIzMmJzFuZvwUVkHcz/9WrV+POnTto0KABFi5cqHUvVdLP0Cz+GTNmYObMmaUb5h+gT58+vAVVERw5cgTz5s1DXFwcatasCX9/fwQGBvI6QCM8ePAACxYswMGDB3H//n24uLjAz88P06dPh62trdzxhBMVFYV+/frp1EeMGIGwsDCo1WosXrwYX331FZRKJVq1aoXly5fzH5xEMvtHNKlERERE9M9Spq9JJSIiIqJ/JjapRERERCQcNqlEREREJBw2qUREREQkHDapRERERCQcNqlEREREJBw2qUQm1KRJEwQFBcny2VFRUVAoFIiKijLpdoOCgjSPjjQXffr0QZ8+feSOQURk1tikEhViy5YtmqdL5f/y9PSEr68vIiIi5I5XLA8ePMDy5cvh4+ODWrVqwcXFBa1bt8a0adNw7do1ueOVuNOnT2PRokVQKpVyRyEiIj3K/GNRiUpDcHAwPDw8oFarce/ePWzfvh1vv/021q9fXyYfnXjjxg0MGjQICQkJ6N+/P0aOHIny5cvj6tWr2LNnD7766ivcu3dP7pgl6syZM1iyZAlGjhyp8/S1vXv3yhOKiIg02KQSGaFHjx5o06aN5vU777yDevXqYdeuXWWuSc3NzcXo0aORkpKC/fv3o1OnTlrLP/74Y8ybN88kn6VWq5GTk1PmHtVpbW0tdwQiIrPH0/1Er8De3h4VKlRAuXLlCl3vyZMnWLBgAbp27Qp3d3dUq1YNPXr0wHfffaezrkKhwIcffogff/wRnTt3houLC1q2bIldu3bprBsbG4vBgwfD1dUVdevWxccff4ynT58alX3//v24fPkyJk+erNOgAoCtrS0WLlyoU7979y7Gjh2LWrVqwd3dHf/+97+RnZ2t98+wb98+dOjQAVWrVsXu3bsBAImJifD390edOnXg4uKCTp06YevWrVrvT0hIgEKhwKpVq7Bp0ya0aNECrq6u6NevH27cuAEAWLNmDZo0aYJq1arBz88PKSkpWts4deoU3nnnHTRu3BhVq1ZF/fr1MWnSJK3T+osWLcLcuXMBAM2aNdNcypF/PW/Ba1JfzLV161a0adMGVatWRYcOHXDixAmjxp2IiIqGR1KJjJCZmYnU1FQAwL179/Dll18iNTUVw4cPL/R9Dx48wMaNGzFo0CCMHj0ajx8/xs6dOzFq1Cjs2rULPXr00Fr/7NmzOHToEMaOHYu33noLmzdvRkBAAJo0aYJ69eppPr9Pnz54/Pgx3n//fTg5OWHbtm04fvy4UX+Ww4cPA8BLs79IpVJh0KBBaNSoEebOnYuYmBhs2rQJzs7OmD17tta6p0+fRkREBPz9/eHi4oK6desiNTUVvXv3Rnp6OgICAlCtWjXs2bMHQUFBUCqVOpPN9u7di8ePH+Pdd99FVlYWVq9ejVGjRsHPzw/79+/HhAkTkJKSgjVr1mDy5Mn49ttvtd6bnp6OMWPGwMXFBZcvX8bmzZvx119/4ciRIwCAfv36ITY2Fnv27MHChQvh7OwMAJoxNiQiIgKpqakYO3YsbG1tERYWhtGjR+PSpUtwdHQ0ejyJiOjl2KQSGcHPz0/rdbly5bBq1aqXzgBXKBT4448/YGNjo6kFBgaic+fOCA0N1WlSr1y5gujoaE2zNHDgQDRu3BjffPMNPvnkEwDAp59+irt37+K7775Dhw4dAORdfqDvqKg+V69eRaVKlVCrVi2j1geAp0+fwtfXFyEhIQCAd999F0qlEps2bdJpUq9evYrIyEg0bdpUUwsJCcHt27cREREBHx8fzTZ8fX0xf/58jBw5Eg4ODpr1b926hd9++01zraiFhQUWLVqE7OxsnDp1SjOeWVlZ+PLLL3H//n1UrlwZADB37lxUqFBBK1Pr1q0RGBiIM2fOoF27dmjcuDGaNGmCPXv2oE+fPnB3dzdqHK5fv45z585pPqtTp07o0qULdu3aBX9/f2OHk4iIjMDT/URGWLJkCfbt24d9+/Zh3bp16NatG6ZMmfLSGf6WlpaahurJkydIT0/HgwcP0LFjR1y4cEFn/c6dO2sdzatatSq8vb01p7oB4MiRI2jWrJmmQQWAChUq4J133jHqz/LgwQPY29sbte6Lxo0bp/W6Y8eOSE1NxYMHD7Tqbdu21WpQ8zM3bdpU06ACedd9BgUF4eHDhzh58qTW+v3799eazNS6dWsAwJAhQ7Qa/latWkGtViMhIUFTy29Q1Wq15gh427ZtAUDvmBfFwIEDNQ0qADRt2hSVKlXS2j9ERGQaPJJKZISWLVtqTZwaMmQIfHx8MH36dPj6+hY60Wbz5s34/PPPcfXqVajVak1dkiSddfUd3VQoFEhPT9e8TkxMRL9+/XTW8/LyMurPYm9vX+Smqly5cnB1ddXJBQDp6elaTW/t2rV13n/z5k29mfMb8ps3b2rVa9asqfW6UqVKAIAaNWrorb94vemtW7cwe/Zs/PjjjzoNdEZGhk6GotC3fxwcHLT2DxERmQaPpBK9AgsLC3Tq1Al37twp9J6iu3btwv/93//Bw8MDn3/+OXbt2oV9+/Zh6NChWg1rPktLS73bKbiuvgZX3/b0qVevHjIzM3Hr1i2j1gfy/ryGFPzc8uXLG71dQ5kNjcPLxkelUmHw4ME4ceIEPvzwQ3zzzTfYu3evZvKWSqUyOturfD4REZkOj6QSvaLc3FwAwMOHDw2us2fPHtSuXRvffvutVmO5ZcuWV/7cWrVq4e+//9apG3sDfl9fX+zcuRPbtm3D1KlTXzlHUbi5uenNHBsbq1luCpcvX8bff/+Nzz//HCNHjtTU9Y2NvkafiIjEwSOpRK/g6dOnOH78OKytrVG3bl2D6+UfeXvxSNuNGzdw8ODBV/7snj174vfff8epU6c0tUePHuGrr74y6v39+/dH48aNsXLlSpw+fVpneU5ODmbNmvXK+fTp1asXLl68iJ9//llTe/r0Kb744gtUqFDB6ElfL6NvvAEgNDRUZ938a1f5xCkiIjHxSCqREX766SfEx8cDyLsF1J49exAXF4cPP/xQc12kPr6+vjhw4ABGjBgBX19fJCUlYcOGDfD09MTly5dfKcukSZOwY8cODB8+HAEBAZpbUBWc0W6IlZUVvvnmGwwcOBB9+/ZF//790aFDB9jY2CAuLg579uzB3bt3sWDBglfKp8+HH36IPXv2YMSIEQgMDISLiwv27t2Ls2fPYuHChVoz+4ujbt268PT0REhICJKSkuDo6Igff/wRSUlJOuu2aNECAPDJJ5/Az88P1tbW6NKlC6pUqWKSLEREVDxsUomMsHjxYs3vbW1t4e3tjZUrV2Ls2LGFvm/kyJG4f/8+NmzYgBMnTqBOnTpYuHAh4uPjX7lJrVq1Kg4dOoQZM2ZgzZo1sLe3x7Bhw9C9e3cMHjzYqG3Url0bP//8M9auXYv9+/fjhx9+QG5uLmrVqoU+ffro3Le0uJydnXHkyBHMnTsXGzduxKNHj+Dl5YWwsDCMGDHCZJ9Trlw5bNu2DcHBwQgNDYWFhQVef/117N69W+eId5s2bRASEoKvvvoK77//PlQqFQ4cOMAmlYhIEJJSqeQV/0REREQkFF6TSkRERETCYZNKRERERMJhk0pEREREwmGTSkRERETCYZNKRERERMJhk0pEREREwmGTSkRERETCYZNKRERERMJhk0pEREREwvl/nVOw+wdtqcEAAAAASUVORK5CYII=\n", "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "\n", "pwc_darkblue = patients_with_colors[patients_with_colors['Color'] == 'darkblue']\n", "pwc_gold = patients_with_colors[patients_with_colors['Color'] == 'gold']\n", "\n", "fig, ax = plt.subplots(figsize=(7,6))\n", "\n", "ax.scatter(pwc_darkblue['Bland Chromatin'], \n", " pwc_darkblue['Single Epithelial Cell Size'], \n", " label='Color=darkblue', \n", " color='darkblue')\n", "\n", "ax.scatter(pwc_gold['Bland Chromatin'], \n", " pwc_gold['Single Epithelial Cell Size'], \n", " label='Color=gold', \n", " color='gold')\n", "\n", "x_label = 'Bland Chromatin'\n", "\n", "y_label = 'Single Epithelial Cell Size'\n", "\n", "plt.ylabel(y_label)\n", "\n", "plt.xlabel(x_label)\n", "\n", "ax.legend(bbox_to_anchor=(1.04,1), loc=\"upper left\")\n", "\n", "plt.xlim(0, 11)\n", "plt.ylim(0, 11);\n", "\n", "plt.show()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Oops. That plot is utterly misleading, because there are a bunch of points that have identical values for both the x- and y-coordinates. To make it easier to see all the data points, I'm going to add a little bit of random jitter to the x- and y-values. Here's how that looks:" ] }, { "cell_type": "code", "execution_count": 11, "metadata": { "tags": [ "remove_input" ] }, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
Bland Chromatin (jittered)Single Epithelial Cell Size (jittered)ClassColor
03.1147962.1043580gold
12.8596416.9464570gold
23.0474262.0258890gold
32.9236392.7201180gold
42.8920192.0883990gold
\n", "
" ], "text/plain": [ " Bland Chromatin (jittered) Single Epithelial Cell Size (jittered) Class \\\n", "0 3.114796 2.104358 0 \n", "1 2.859641 6.946457 0 \n", "2 3.047426 2.025889 0 \n", "3 2.923639 2.720118 0 \n", "4 2.892019 2.088399 0 \n", "\n", " Color \n", "0 gold \n", "1 gold \n", "2 gold \n", "3 gold \n", "4 gold " ] }, "execution_count": 11, "metadata": {}, "output_type": "execute_result" } ], "source": [ "def randomize_column(a):\n", " return a + np.random.normal(0.0, 0.09, size=len(a))\n", "\n", "jittered = pd.DataFrame(\n", " {'Bland Chromatin (jittered)':randomize_column(patients['Bland Chromatin']),\n", " 'Single Epithelial Cell Size (jittered)':randomize_column(patients['Single Epithelial Cell Size']),\n", " 'Class':patients['Class']})\n", "\n", "\n", "jwc = pd.merge(jittered, color_table, on='Class')\n", "\n", "jwc.head()\n" ] }, { "cell_type": "code", "execution_count": 12, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAqkAAAGTCAYAAAALL4uRAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Il7ecAAAACXBIWXMAAAsTAAALEwEAmpwYAACE40lEQVR4nO3deVxU5f4H8M9hAEGWQERAkREB9z28brnmLzPRcKEyW/QWLmVlVi431Bauii1mWu6Vda2bK26ZLS65VpilZhoKjqKgiCCLbLP8/uDOyDBnhgFm5pyRz/v16vWK55w58/Uww3zmOc/zHCEvL08HIiIiIiIZcZG6ACIiIiKiqhhSiYiIiEh2GFKJiIiISHYYUomIiIhIdhhSiYiIiEh2GFKJiIiISHYYUomIiIhIdhhSCQCQmpoqdQlOjeevbnj+ao/nrm54/ojkiyGViIiIiGSHIZWIiIiIZIchlYiIiIhkhyGViIiIiGTHVeoCiIiISDpqtRpFRUVSl0H1kJeXF1xdzUdRhlQiIqJ6Sq1Wo6CgAH5+fhAEQepyqB7R6XTIy8uDj4+P2aDKy/1ERET1VFFREQMqSUIQBPj5+VnsxWdIJSIiqscYUEkq1b32GFKJiIiISHYYUomIiIhIdhhSiYiIiEh2GFKJiIioXlq/fj2aNWsmdRkAgKVLl6Jjx451Ps7Bgwfh5+eHnJwc0e0qlQp+fn44ceKE2WNYs48jMKQSERGRU7p+/TpmzpyJLl26oEmTJmjbti3GjBmD7777TurSyAa4TioRERE5HZVKhQcffBDe3t6YN28eOnToAK1WiwMHDmD69Ok4ffq0Q+ooKyuDu7u7Q56rOmVlZVKXYFPsSSUiIqI6UanyER+/FzExOxEfvxcqVb7dn/PVV1+FTqfDvn37MHLkSERFRaF169aYOHEiDh06BAC4fPkyxo0bh9DQUISGhuKJJ57AlStXLB73008/RdeuXREYGIiuXbti3bp1Rtv9/PywevVqPPHEE2jatCneeuutWtW/ZMkStGrVCs2aNcOkSZNQWFhotP23337DyJEj0bJlSzRv3hwPPvggfvnllxrXUlpainHjxqFfv37Izs42tJ8/fx4PPvgggoKC0L17d+zdu9dsrWJDCMSGBJw9exaPPPIIQkNDERkZiWeeeQbXrl2r8bnRY0glIiKiWlOp8hEbuxsbN17AoUOZ2LjxAmJjd9s1qObm5uKHH35AfHw8vL29Tbb7+flBp9Nh3LhxyM7Oxvbt27Fjxw5kZWVh3Lhx0Ol0osfdsWMHXnvtNUyZMgVHjx7F5MmT8corr2D37t1G+yUlJeGBBx7AkSNH8OyzzwIAmjVrZvG/MWPGGB6/detWJCYmYvbs2Thw4ACioqLw8ccfGz1HQUEBHn30UezevRs//vgjOnbsiLi4OJOxpmK16OXn52P06NHIzc3Fzp07ERgYaNg2b948TJo0CQcPHsSAAQPw+OOP4+rVq1acfXFZWVl46KGH0LZtW/z4449ITk5GYWEhxo4dC61WW6tj8nI/ERER1VpiYgrS040DaXp6PhITU7B69SC7PGdaWhp0Oh1atWpldp/9+/fj9OnTOHHiBJRKJQBgzZo16Nq1Kw4cOIABAwaYPGbZsmV49NFHMXHiRABAZGQkfv/9dyxZsgRDhw417Ddy5Eg89dRTRo89ePCgxZo9PDwM/798+XKMHTsWEyZMAFDRK3zw4EGkpaUZ9unfv7/R4xctWoTt27fjhx9+wKOPPmq2lsuXLwMAbty4gYkTJyIkJASfffaZ0fMDwD//+U+MHDkSQEXQ3bt3Lz755BMkJCRY/HeYs3btWnTo0AFvvvmmoW3lypVo0aIFTpw4gXvvvbfGx2RIJSIiolrLzLwt2p6VJd5uC+Z6Qis7d+4cQkJCDAEVAFq0aIGQkBCcPXtWNKSeO3cO48aNM2rr1auXSU9q165dTR7bsmVLK6uveJ4nn3zSqK179+5GITU7Oxv//ve/cfDgQWRnZ0Oj0aC4uBgZGRnV1gIAo0aNQqdOnfDFF1/A1dU07nXv3t3w/y4uLrj33ntx9uxZq/8NVf3xxx84cuSI6GoJ6enpDKlERETkWCEhDUXbg4PF220hIiICgiDg77//NruPTqcze9tNS7fjFNtWtc3Ly8tkn+qWsurVqxc2bdpkcZ/KpkyZguvXr2P+/PkICwtDgwYNMGLECJPJUWK1AMCQIUOwdetW/Pnnn+jcubPVzyvGxaVidGjlLwdqtdpoH61WiwceeACJiYkmj688zKAmGFKJiIio1hISopGSkm10yT883BcJCdF2e05/f3/cf//9WL16NSZNmmQyLjUvLw9t2rTB1atXoVKpDL2pFy9eRGZmJtq0aSN63NatW+PYsWNGvZxHjx41u39lNbnc37p1a6SkpBg9T0pKitH+x44dw8KFCzFkyBAAFctt1WQS0uuvvw5/f3/ExsZi27Zt6NSpk9H2lJQUw5ACnU6H3377DQ8//LDosRo3bgygYtyp/v9PnTpltE/nzp2xdetWNG/eHG5ublbXaQlDKhEREdWaUumL5OShSExMQVbWbQQHN0RCQjSUSl+7Pu+7776LIUOGYODAgXj99dfRvn176HQ6HDx4EIsXL8apU6fQoUMHTJw4EUlJSdDpdJgxYwY6d+6Mfv36iR7zhRdewPjx49GlSxcMGjQIP/zwAzZu3Igvvvii2npqcrl/8uTJmDx5Mrp164b77rsP27Ztw/Hjx+Hn52fYJyIiAhs2bEB0dDRu376NuXPn1nipqzlz5kCn0xmCauWbBXzyySeIjIxEu3btsGbNGly+fBn//Oc/zf7bQkNDsXDhQrzxxhu4dOkS3nnnHaN9nn32Waxbtw4TJkzAtGnT0LhxY1y8eNEwSczHx6dGtQMMqURERFRHSqWv3SZJmdOiRQscOHAA7733HubNm4fMzEw0atQIHTp0wOLFiyEIAtavX4+ZM2ciJiYGQMVkpEWLFpm93B8TE4NFixZh6dKlmD17Npo3b4733nvPaNKULYwaNQoXL17E22+/jeLiYgwdOhTPPfccvvzyS8M+y5Ytw7Rp0zBgwAAEBwdj1qxZZu8iZcncuXOh0+nw8MMPY9u2bfD1rfjyMG/ePHz00Uf4448/0Lx5c/znP/8xO2TBzc0Na9euxSuvvIL77rsPHTt2xNy5c40mcIWEhGDPnj148803MXr0aJSWliI0NBQDBw5EgwYNalw3AAh5eXnVjz6mu15qaiqioqKkLsNp8fzVDc9f7fHc1U19P3+3bt3CPffcI3UZVI9Zeg2yJ5WcmkpVscxJZuZthIQ45hKTs+E5sh7PlW050/l0plqJ6guGVJKF6j4gxLYDQGzsbqPB+ikp2UhOHsoPl//RL7LNc1Q9ZzxXKlU+5sw5g8LCc7ILVs50Pp2pVqL6hCGVJFfdB4S57W3b+jl8AWl9vWKBWY6kWGTbGalU+Rg+fBcuXTK+LaGcz5Xcg5UzvfacqVai+kTS26IePnwYjz32GNq2bQs/Pz+sX7/eaLtOp8OCBQvQpk0bBAcHY9iwYfjrr78kqrZuBLUKnrnx8LoRA8/ceAhqldQlyYalDwhL23/99bro8ey5gLS52/9duVJst+esCykW2XY2+t9p1YCq9913lxx2L/KaqO59IzW5v/b095qfPPkE9u8Xv5e7XGolqq8kDalFRUVo164dFi5cCE9PT5PtS5YswUcffWS4XVdgYCBGjhyJgoICCaqtPUGtgtfNWLiXbIRr+SG4l2yE181YBtX/qe7DzNz20lKNaLs9F5A2FwxWrEi323PWhRSLbDsbsd9pZbdulWPjxgsYNmynrIKqufeFHEK1SpWPS5fE/07L4bVX+cvm8eO3kJ1dIrqftzcvNhJJSdKQ+sADD2Du3Ll4+OGHDXcz0NPpdFi+fDmmTZuGhx9+GO3atcPy5ctRWFhYozs2yIFHQSIUGuMQo9Ckw6PA9K4M9VF1Qcrc9vz8cpO20FAvu15+NxdmsrPLRNullpAQjfBw40u/9l5k29mYC3tVZWQUYejQHYiJ2Sl5CAQAX1/xxbL1oTo2drckNVrqmZbLa6+6LyZ6lu5KRET2J9uviSqVCteuXcOgQXfGA3l6eqJ37974+eefMWHCBNHHpaamOqpEq7XySIO7yJkuKUxD6g351CvVuRs3rjGOHr2CjIw7vRmhoR4YN64xUlNTMW5cY+zcmY7iYm21x2rZsgHKyq4hNdX6u3JY68qVYvz5p/gadenpRXjssW2YPDkczZqZXhWQ0uLFbbFiRTqys8sQGOiOyZPD7XaO6kKq15+3t3iPvJirV2/j6tWKUHv06BUsW9ZZst93YaH48AS99PR8zJy5D2+/3c5BFVWYM+eMaAAMCWmAxYvbyuK1l5Z2w6r9rl3Ll/QzpT4vjUUEWBlS09PTsXPnThw7dgx///03cnJyIAgCAgIC0KpVK/To0QMPPfQQIiIibFaY/tZfVe/3GhgYiMzMTLOPk+Ob2iO3JVBy3LTduyWimsujXinXCoyKAnbtamH2biVRUUD79mlIScmu9lg6XQO7/TsWLdprNijfvFmOb7+9jnPnSmQzcUUvKgoYMMD4dnhyW25HytdfUlIQzp0znoDk4iJAq7W8hHRGRgnWr7/h8El6+t+TVnuu2scXFSkccl4r13nunHgPZWRkI5PXoRRUqnxkZ1v3xaRlywBZfqYQ1RcWQ+q3336LDz/8EMeOHYNOp0N4eDhatGiBTp06QafTIS8vD3/++Sd27dqFefPmoUePHnjxxRdtemeGqpdbdDqd012CKfFJgKI8xeiSv0YRjhKfBAmrkpfq7lYSHu5rVUi153g3ay4LO8OMYLnPCnc0sVs6Zmffxv795r8M6zlikl7l39PRo1no2LERCgrUZsd8VuaI8Z9idUpVS3WqmyRXmVyGJhDVZ2ZD6uDBg3Hq1Ck8+OCD+PTTT9G/f3+je8pWlpeXh71792Lbtm0YP348OnXqhO+//75OhQUFBQEArl+/jtDQUEP7jRs3THpX5U7nqkRRo2R4FCTCRZMFrSIYJT4J0LkqpS7NaSQkRCMlJdvog9DVVYBafae3y94fKubGxlYlpxnBYj1xXG7HVNUvSSpVPoYN24mMjCKLj3P0JL2MjCKjmqq+BypzVMiyZnynXAKfNbXec48bHnggTPKrC+QY69evx4wZM3DlivgKD3Ln5+eHdevW4eGHHxbdnpOTg4iICOzYsQN9+/Z1cHV1Zzak9urVC//5z38QHBxc7UH8/PwwatQojBo1CpmZmfj444/rXJhSqURQUBD27duHbt26AQBKSkpw9OhRvPXWW3U+vqPpXJUo9l8tdRlOS6y3a/z4Nvjss7OiQwTsQSwoi5FDjxFgvsc0IED8HspyCtdSUyp9sWtXjOH15u3tilOnbhoFRHsHL2t67tVqHUJCGiAyshG8vV0hCAIKCsod8n6ors7AQA+0aePv0FqqY805feCBsHr7Zc0ZXb9+He+99x727NmDq1evIiAgAO3bt8fEiRPxwAMPSF0e1ZHZkPr222/X6oAhISFWP7awsBBpaWkAAK1Wi4yMDJw8eRL+/v5o3rw5pkyZgvfeew9RUVGIjIzEu+++Cy8vL4wZM6ZWtZH8xiLWhNiQgD59mjr0+SsHZSmCS02Y6zHVaLxF95dLuJYLsd5Vc+Om7cHanvumTT2xY0eM3eqojrk6BwxoJruwV905ldP7l6qnUqnw4IMPwtvbG/PmzUOHDh2g1Wpx4MABTJ8+HadPn3ZIHWVlZXB3d3fIc9U3ki5BdeLECfTr1w/9+vVDcXExFixYgH79+mH+/PkAgJdeegnPPfccXnvtNQwcOBBZWVnYsmULfHx8pCzbaZlbiF7qpXSciT647NgRg6++ehC7dsUgLi4C997rh7i4CFmN6zTXa9SkiSeXpaqFyr/71asH2f33LLZ8mJjAQGk/HJ1pmTOxWj09XRAdHSi796+zkeKGNa+++ip0Oh327duHkSNHIioqCq1bt8bEiRNx6NAhAMDly5cxbtw4hIaGIjQ0FE888US1l/Y//fRTdO3aFYGBgejatSvWrVtntN3Pzw+rV6/GE088gaZNm9b66u7777+PqKgoNGvWDJMmTcLChQvRsWNHw3atVotFixahffv2aNKkCXr37o1du3ZZPOZvv/2G/v37IygoCH379kVKijxu7lFbZntSv/rqq1odcOzYsVbv27dvX+Tl5ZndLggCZs+ejdmzZ9eqFjJmaSzijBnNJarKuemDi5Sz080x12sUHu6LtWujHdorSDVXtefex8cNJ0/mmPTcT54cLmGV4kNx5Pp6Eqt13LjGslh1wJnpb1hjmBxcDijKU1DUKNlucy9yc3Pxww8/ICEhAd7epleH/Pz8oNPpMG7cOHh4eGD79u0QBAGvvfYaxo0bh3379olOwt6xYwdee+01zJ8/H4MGDcKPP/6IV155BU2aNDGaFJ6UlIS5c+ciMfHOeufNmjWzWHOvXr0M67xv3rwZSUlJeOedd9C7d29s374dH3zwAe655x7D/suXL8fSpUvx/vvvo2vXrvj666/x5JNPYv/+/ejUyfQ1W1RUhEceeQR9+vTB8uXLkZmZ6fT5yWxIfe6550za9L9QnU4n2g7ULKSSY8n9NoVkW2JjaPU9XNWtpkDyYM2Qg7Iy6de7dabXU9Va5bi2trOxdMMae83FSEtLg06nQ6tWrczus3//fpw+fRonTpyAUlkRltesWYOuXbviwIEDGDBggMljli1bhkcffRQTJ04EAERGRuL333/HkiVLjELqyJEj8dRTTxk99uDBgxZr9vDwMPz/ihUr8PjjjxuOMX36dBw8eBDnz583qmXq1KmIi4sDALz++us4cuQIli1bhlWrVpkcf+PGjSgrK8NHH30Eb29vtGvXDq+88gomTZpksS45MxtS//jjD6OfCwoKMHnyZPj4+GDSpEmIjIyETqfD+fPnsXLlShQVFWHFihV2L5hqj7fIrF+cqYeLrCMWBqVeGJ/IRSO+XJuLJstuz1m1s0zMuXPnEBISYgioANCiRQuEhITg7NmzoiH13LlzGDdunFFbr169sHv3bqO2rl27mjy2ZcuWVlYP/P333yYh99577zWE1Pz8fGRmZqJnz54mtXz33Xeixzx37hzat29v1LP8j3/8w+qa5MhsSA0LCzP6+cUXX4S/vz+2bdtm1HPaoUMHjBgxAg8//DBWrlyJJUuW2K9aqhNLPWty6I0h23OmHi4ick5aRQhgepdqaBXVrw5UWxERERAEAX///bfZfSytq25pvXWxbVXbvLy8TPapyeX+6mqwxNzjrAnuzsbqiVM7duzA8OHDRU+Oi4sLRowYgR07dti0OLItfc9aXFwE+vYN4UQBIiKqsxKfBGgUxmOj7X3DGn9/f9x///1YvXq16C2C8/Ly0KZNG1y9ehUq1Z1JXBcvXkRmZibatGkjetzWrVvj2LFjRm1Hjx41u39lBw8etPjfhx9+aNi3VatW+O2334weX/lnX19fhISEiNbSunVr0edv06YNzpw5g6KiO+PWf/3112rrljOrbosKAGq1GpcuXTK7/eLFiygvF/kqRbLCnjUiIrIlqW5Y8+6772LIkCEYOHAgXn/9dbRv3x46nQ4HDx7E4sWLcerUKXTo0AETJ05EUlISdDodZsyYgc6dO6Nfv36ix3zhhRcwfvx4dOnSBYMGDcIPP/yAjRs34osvvqi2nppc7p88eTKef/55dO3aFb1798bOnTuRkpJidNOkF154AQsWLEBERAS6dOmCr7/+GkePHsX+/ftFjzlmzBi8/fbbmDp1KmbMmIGsrCy89957VtckR1aH1EGDBmHVqlXo1KkTxowZYzSJauPGjVizZo1Nb4dKREREzkGKG9a0aNECBw4cwHvvvYd58+YhMzMTjRo1QocOHbB48WIIgoD169dj5syZiImpWEu4f//+WLRokdlL5jExMVi0aBGWLl2K2bNno3nz5njvvfdsnm9Gjx6Nixcv4s0330RxcTFiYmLwz3/+E998841hn8mTJ6OwsBDz5s3D9evXERUVhc8//1x0Zj8AeHt74+uvv8b06dPRv39/REVF4Y033nDqCe1CXl6eVYMYrl27hhEjRiA1NRWBgYEIDw+HIAhIS0sznLzt27dbdYcqkh85LqHkTHj+6obnr/Z47uqmvp+/W7duGS17RNIZN24c1Go1vv76a6lLcShLr0Gre1KDgoLw008/4bPPPsN3332Hy5cvQ6fToUOHDnjggQfw9NNPGy2vQERERESmbt++jbVr12Lw4MFwdXXF9u3b8c033+Dzzz+XujRZsTqkAkCDBg0wadIkp15zi4iIiEhKgiDghx9+wPvvv4+SkhK0bNkSK1euxPDhw6UuTVZqFFIBoLi4GCdOnEB2djb69OmDxo0b26MuIiIioruSp6cntm3bJnUZsmf1ElRAxR0SWrdujWHDhmHChAn4888/AQA5OTkICwtjNzURERER2YTVIXX9+vWYPXs2Bg8ejGXLlhktGhsQEICBAwdi69atdimSiIiIiOoXq0PqRx99hCFDhuCTTz4RXYqhS5cuOHfunE2LIyIiIvu6G+9URM6hutee1SH1woULGDJkiNntAQEByMnJsb4yIiIikpSXlxfy8vIYVMnhdDod8vLyRG8xq2f1xCkfHx/cunXL7PYLFy5wEhUREZETcXV1hY+PD/Lz86UuheohHx8fuLqaj6JWh9R+/fph/fr1mDJlism2K1euYN26dXj44YdrVyURERFJwtXVlQv6kyxZfbk/ISEBN27cwIABA7B69WoIgoDvv/8eb7zxBvr06QM3NzfMmDHDnrUSERERUT1hdUht2bIlvv32WwQHByMpKQk6nQ4fffQRlixZgs6dO+Pbb79Fs2bN7FkrEREREdUTVl3u12q1uHLlCpo0aYKtW7ciLy8PaWlp0Gq1aNGiBceiEhEREZFNWdWTqtFo0LVrV6xfvx4A4Ofnh27duiE6OpoBlYjuGipVPuLj9yImZifi4/dCpeJkEiIiqVjVk+rm5obg4GAIgmDveoiIJKFS5SM2djfS0+8E05SUbCQnD4VS6SthZURE9ZPVY1KfeuopfPnllygpKbFnPUREkkhMTDEKqACQnp6PxMQUiSoiIqrfrF6CKjw8HDqdDt27d8fYsWPRokULeHp6muw3cuRImxZIROQImZm3RduzssTbpaRSVYTnzMzb8PbWICkpiL29RHTXsTqkTpw40fD/77zzjug+giAwpBKRUwoJaSjaHhws3i4VsWEJ587t5rAEIrrrWB1Sd+zYYc86iIgklZAQjZSUbKPwFx7ui4SEaAmrMmVpWMLq1YMkqoqIyPasDqn33XefPesgIpKUUumL5OShSExMQVbWbQQHN0RCQrTseiedaVgCEVFdWB1S9YqLi3HixAlkZ2ejT58+XIKKiO4aSqWv7HsjnWVYAhFRXVk9ux8AVqxYgdatWyMmJgYTJkzAn3/+CQDIyclBWFgYPv/8c7sUSUREFRISohEebty7K8dhCUREdWV1SF2/fj1mz56NwYMHY+nSpdDpdIZtAQEBGDhwILZu3WqXIomIqIJ+WEJcXAT69g3Bgw824aQpIrorWX25/6OPPsKQIUPwySef4ObNmybbu3TpgtWrV9u0OCIiMlV5WEJqaioDKhHdlazuSb1w4QKGDBlidntAQABycnJsUhQRERER1W9Wh1QfHx/cunXL7PYLFy5wEhURERER2YTVIbVfv35Yv349SktLTbZduXIF69atw+DBg21aHBERERHVT1aH1ISEBNy4cQMDBgzA6tWrIQgCvv/+e7zxxhvo06cP3NzcMGPGDHvWSkRERET1hNUhtWXLlvj2228RHByMpKQk6HQ6fPTRR1iyZAk6d+6Mb7/9Fs2aNbNnrURERERUT9RoMf/WrVtj69atyMvLQ1paGrRaLVq0aMGxqERERERkU1b3pCYlJeHMmTMAAD8/P3Tr1g3R0dGGgPrXX38hKSnJPlUSERERUb1idUhduHCh4Q5TYhhSiYiIiMhWanRbVEsKCwvh5uZmq8MRERERUT1mcUzq6dOncerUKcPPR48ehVqtNtkvLy8Pn3zyCSIjI21fIRERERHVOxZD6s6dOw2X8AVBwKeffopPP/1UdF8fHx/eFpWIiIiIbMJiSH3qqacwePBg6HQ6PPDAA5g1axbuv/9+o30EQUDDhg0REREBd3d3uxZLRERERPWDxZDatGlTNG3aFACwY8cOtGnThstNEREREZHdWT1x6vnnn8cvv/xidvu3336Lzp0726QoIiIiIqrfrA6ply5dQlFRkdntRUVFuHz5sk2KIiIiIqL6rUZLUAmCYHbb+fPn4ePjU+eCiIiIiIgsjkn98ssv8dVXXxl+fvfdd7Fu3TqT/fLy8nDmzBkMGTLE9hUSERERUb1jMaQWFRXh2rVrhp9v3boFrVZrtI9+dv/TTz+NWbNm2adKIiIiIqpXLIbU+Ph4xMfHAwA6deqEhQsX4qGHHnJIYURERLakUuUjMTEFmZm3ERLSEAkJ0VKXREQWWAyplZ08edKedRCRnYh9MCuVvlKXReRQKlU+YmN3Iz0939CWkpKNxYvbIipKwsKIyCyrQyqRlJw5aElZu7kP5uTkoU5z/uTAmV9/VCExMcXofQAA6en5WLEiHQMGdJKoKiKyxGxI9ff3h4uLCzIzM+Hu7g5/f3+Ls/uBivGpOTk5Ni+S6i+VKh+zZx/Fjz9eQWmpxtAuVdCqaViROiSa+2BOTEzB6tWD7P78dwOpf4dkG5mZt0Xbs7PLHFwJEVnLbEidMWMGBEGAq6ur0c+OpNFosGDBAmzYsAHXrl1DUFAQHnnkEcyaNctQF929xMKBnhRBy1JYuXKlGIsW7TUJr1KHRLEPZmWzHDz70FZ43XgfWkUISnwSoHNV2r0WZ6RS5WP48F24dKnQqF3qoF/5y5K3twZJSUEMzNUICWko2p6eXoT4+L3sHSeSIbNJb/bs2RZ/doQPPvgAa9aswfLly9GuXTv8+eefmDJlCtzd3TFjxgyH10OOJRbwKsvKEu8ZsRdzgXPWrCM4dSobGRklhnZ9eDXXe+Oo2n18jN/iymY5+GHtKkQqbwLlAMoBRXkKiholM6hWof9SUjWg6jn69acn9mXp3Lnd7NmtRkJCNFJSsk3ewzdvlmPjxgvsHSeSoRot5u9ov/zyCx588EEMHToUSqUSDz30EIYOHYrjx49LXRrZiaBWwTM3Hl43YvDsQ+9C2cz88JHgYPGeEXsxFzhTUowDKnCnp81c740jalep8nHihPH5S3xpT0VArUShSYdHQaLd65EzlSof8fF7EROzE/Hxew09lZa+JKlUBUb7O6rGwYO3me2dJ/OUSl8kJw9FXFwEAgM9TLbzHBLJj9me1MOHDwMA+vTpY/RztQd0dUVAQAAiIyPrXFzPnj2xdu1a/P3332jVqhXOnj2LgwcP4uWXX67zsUl+BLUKXjdjodCkAwAe6An8sPYsBj8zEaorAUb7hof7Onz5GHOB05ysrNtYtqyfSe+No2pPTEwx6e1r2kQ8TLlosuxej1yZG8bRqFEDs48RBODSpUJDL6u9e+EsDX3Rk6pn15kolb5YvXoQYmJ2Ijs702Q7zyGRvJgNqTExMRAEAVlZWXB3dzf8bK1mzZrhiy++QJcuXWpd3LRp01BYWIgePXpAoVBArVbj1VdfxbPPPmv2MampqbV+vvpO6nMX3mAOFG7pRm2RyptIfGkPnpzxOADA3V1Az57+mD49CmVl15Caek3sUHYxblxjHD16xajXNDTUAy1beiE7u8Rkfy8vDcrKrmHx4rZYsSId2dllCAx0x+TJ4Q6pPS3thknb1eviIerWbS+kS/z7l+r1N2fOGdGeyZIS8ZAqCIBOB5P9Z87ch7ffbuewGqs6f/4m9u8/iWbNPO1Sw93E21sj2u7lpZH872BlUVwbi+o5syF1x44dAAB3d3ejn6uj0WiQlZWFDz74ANOnT8fevXtrXdyWLVvw3//+F2vWrEGbNm1w6tQpzJo1C2FhYXjqqadEH8M3de2kpqZKfu68bhRWjJOsonP7cvTtG4LgYGmX/omKAnbtamHoodTXAwDDhm0zCq/h4b5IShoIpdIXUVGQZImbli0v4/jxW0ZtCUuGoGcnldElf40iHG6BSYiScEyqlK+/wsJzou2lpUBoqBcyMooMbV5erigqUovuX1SksNu/wVyNlWVmluLll//iuEorJCUF4dy53SZXOPTvWSKSB7Mh9b777rP4c3WKi4sxc+bM2lX1P3PnzsXUqVMxevRoAED79u1x+fJlLF682GxIJeelVYSIhtTW7dpix44YxxckQn+5sKplyzpj/fobRuFV6g+7hIRoHD2aZRSyVFcC8OTr0/DNut/g45EDrSK43s/uNzeM4+bNUjRs6IqhQ5ujsFCN4OCGSE/PR0pKtuj+9hxnbO1QE6lXHXAW+vGpiYkpSEvLQcuWAbJ4zxKRMbut4/TII49g0KC6/aG8ffs2FAqFUZtCoYBWq63TcUmeSnwSoChPMYxJBSp6+Up8EiSsyjrNmnnKLhgolb7YtSsGs2cfxa+/XgcAREcHYuHC3nAJfRFF1Ty+vjA36xsAMjKK0KtXML766kEAQHz8XtGQ6uXlatdxxmI1NmigMFo7WI/jKq2j/8Iph6tIRCTO7Oz+xMRE5Obm1viAOTk5SExMRMOGDREWFlan4h588EF88MEH2LNnD1QqFXbs2IGPPvoIMTHy6FUj29K5KlHUKBllHnFQu/VFmUccl0aqI6XSF19+OQSpqU8iNfVJfPXVg+wtqkLfqyY24xswDn0JCdEIDzc+f15ertiwYYhdz2vlmel9+4YgLi4C99/fTHRfR696QURkL0JeXp5ObEO/fv2QlpaGESNGYMyYMejTpw8aNBCfSFBSUoKDBw9i8+bN2LFjB6KiorB///46F1dQUIB///vf2LlzJ27cuIGgoCCMHj0aM2bMgIeH+AcK1Q57E+qG569u5HD+4uP3YuPGCybtcXERRr3k+uWppB7aITbjPzzcl2NSa0gOrz0iEmc2pALA1q1bsXTpUpw4cQJubm5o3bo1lEol/Pz8oNPpkJeXB5VKhXPnzkGtVqNLly548cUXMXLkSEf+G8gG+Ie6bnj+6kYO588ZQ59KVbGqQFGRQjZjoZ2NHF57RCTOYkjV+/PPP7Fz5078/PPP+Pvvv3HzZsXM4EaNGqF169bo0aMHhg0bhvbt29u9YLIP/qGuG56/upHL+ZNLL2lNyOXcOSuePyL5smriVPv27RlAieiuZ271BiIicjxZ3xaViIiIiOonhlQiIiIikh2GVCIiIiKSHYZUIiIiIpIdhlQiIiIikh2GVCIiIiKSnVqF1IyMDPz+++8oLCy0dT1ERERERDULqTt37kS3bt3QqVMnDBo0CMePHwcA5OTkoHfv3tixY4ddiiQiIiKi+sXqkLpnzx489dRTaNy4MWbOnAmd7s6NqgICAhAaGoovv/zSLkUSERERUf1idUhdtGgRevToge+++w7x8fEm27t3745Tp07ZtDgiIiIiqp+sDqlnzpzBqFGjzG4PCgrCjRs3bFIUEREREdVvVodUd3d3lJaWmt1++fJl+Pr62qQoIiIiIqrfrA6pPXv2xNatW0W35efnY/369ejbt6/NCiMiIiKi+svqkDpr1iz8+eefiI2Nxe7duwEAJ0+exCeffIL+/fsjPz8fM2bMsFuhRHKkUuUjPn4vJk8+gfj4vVCp8qUuiYiI6K7gau2OXbt2xaZNm/Dyyy9j6tSpAIC5c+cCACIiIrBp0ya0bt3aPlUSyZBKlY/Y2N1IT68IpseP30JKSjaSk4dCqeTQFyIiorqwOqQCwH333Ydff/0Vp06dwoULF6DVahEeHo4uXbpAEAR71UgkS4mJKYaAqpeeno/ExBSsXj1IoqqIiIjuDjUKqXodO3ZEx44dbV0LkVPJzLwt2p6VJd5ORERE1rN6TKq/vz9atWqFw4cPi27fsGEDGjVqZLPCiOQuJKShaHtwsHg7ETkH/VjzmJidHGtOJKEa3Ra1tLQUsbGxWL58ub3qITIh1w+MhIRohIcbjz0ND/dFQkK0RBURUV3px5pv3HgBhw5lYuPGC4iN3S2bvztE9UmNLvfPnz8fv/zyC/71r3/hxIkT+PDDD+Hh4WGv2ohMJicBkM3kJKXSF8nJQ5GYmIK0tBy0bBmAhIRoyesi+1OpKsYeZ2beRkhIQ9n83uValzPhWHMi+ahRSHV3d8eSJUvQpUsXzJo1C+fOncN//vMfNG/e3F71UT0n9w8MpdIXq1cPQmpqKqKioqQuxwgDi33I9YuTXOtyNhxrTiQfNbrcrzdhwgRs374dWVlZGDBgAA4cOGDruqieEdQqeObGw+tGDDxz4yGoVQDk/4Ghr7uVx2SjuqXGS5b2Y+mLk5TkWpdch+uYw7HmRPJRq9n9ANCjRw/s378fTz75JEaPHo1evXrZsi6qRwS1Cl43Y6HQpFc0lAOK8hQUNUqW9QdG5brdXQGUHDfUrXNVSlqb3HugnZlcvzjJsS5n7N1NSIhGSkq2Uc0ca04kjVr1pOqFhITgm2++wdixY3Ho0CFb1UT1jEdB4p2A+j8KTTo8ChJlPTnJUt1Sk2NgcRbV9fzJ9YuTHOuSa++uJfqx5nFxEejbNwRxcRGyDtVEdzOre1L/+OMPNG7c2KTd3d0dS5cuxYgRI5CdnW3T4qh+cNFkmmnPMpqclJV1G8HB8hlbaaluqckxsDgDa3r+5NrTJse6nPXLkn6sORFJy+qQGhYWZnH7//3f/9W5GKqftIoQoFysPRiAfD8wqqtbSnIMLM7AmmEScv3iJMe6+GWJiOrCbEjVL9rfp08fo5+ro9+fyFolPglQlKcYXTrXKMJR4pMgYVXiKs+Y79R2EN5/+Rc0EO5MlpJL3XIMLM7A2p4/uX5xkltd/LJERHVhNqTGxMRAEARkZWXB3d3d8LM5Op0OgiDg5s2bdimU7l46VyWKGiXDoyARLposaBXBKPFJkHzyUVVVLwUfOgScPBmP7WtToNBdhod3S1nVLbfA4gzY82db/LJERHVhNqTu2LEDQMWY08o/E9mDzlWJYv/VUpdhkdil4EM/N8CkN5/CjBnNEdVcXuukUs2x58/2+GWJiGrLbEi97777LP5MVN846yQQsh57/oiI5KPW66QCwJUrV5CVlYWIiAj4+fnZqCQieeKl4PqBPX9ERPJgcZ3UlJQUJCUlmSwtde3aNcTExKBjx474v//7P0RFRWHevHl2LZRIanJes5WIiOhuYzGkrl27Fl988QUCAwON2p9//nkcPnwYvXr1wvPPP482bdpg6dKl+Oqrr+xaLJGUuMg3ERGR41i83J+SkoJhw4YZtaWnp+PHH3/EoEGDsHnzZgBAeXk5Bg4ciC+++AJjx461X7VEEuOlYCIiIsew2JN67do1REUZz1jes2cPBEHA+PHjDW1ubm4YM2YMzpw5Y5ciiYiIiKh+sRhSgYr1Tyv75ZdfAJgu2h8YGIji4mIblkZERERE9ZXFkBoeHo5jx44Zflar1Th48CBatWqFRo0aGe2bk5ODxo0b26dKIiIiIqpXLI5JHTt2LBISEhAVFYXevXtj06ZNyMnJweTJk032PXz4MCIjI+1WKBERERHVHxZD6jPPPIN9+/YhKSkJgiBAp9Ohb9++eP755432u3z5Mvbu3Yu5c+fatVgiIiIiqh8shlQ3Nzd8/fXXOHHiBNLT0xEWFoboaNM1IcvLy7FmzRqTcapERERERLVh1R2nunbtiq5du5rd3rJlS7Rs2dJmRRERERFR/Vbt7H4iIiIiIkdjSCUiIiIi2WFIJSIiIiLZsWpMKhFZduVKMRYt2ovMzNsICWmIhIRoKJW+UpdFRETktBhSyamoVPlITEyRVRhUqfIxdeofyMgoMbSlpGQjOXmo5LURERE5K4ZUchoqVT5iY3cjPT3f0CaHMJiYmGIUUAEgPb0iTK9ePUiiqpyHSpWPOXPOoLDwnGy+eDgD/Re2tLQbaNnyMs8bEd11zIbUpKSkGh9MEATMmDGjTgURmZOYmGIUUAF5hMHMzNui7VlZ4u2OIsde56rk+sUDqKht9uyj+PXX6wCA6OhALFzYW/K6ANPzdvz4LdmcNyIiWzEbUhcuXFjjgzGkkj3JNQyGhDQUbQ8OFm93BDmHv8rk+sVDpcrHsGE7kZFRZGjbvfsyTp3aiV27YiQ/h3I9b85G34ufnf0nsrOL0aSJJ8LDfWX5hY6oPjIbUnNzcx1ZB9lBbXrS5Nz7JrcwqD9X6en58PR0QXGx1rCtQQMFiorKoVLlS3L+nCXEyO2Lh/53un//FWRnl5hsz8goksU5TEvLF23/66+bAOT9PpYLsS9yly4VIiUlW5Zf6IjqI45JvUvVpidNLr1v5j5gExKikZKSbVSfvtfD0cTOlUIhQKPRAQBKSzX45ptL+OuvPEk+7MyFv6rBVWpy+uIh9jsVI3XPPQBkZxeLtv/1Vx4OH76KqVMPSv4+lqPKf1suXSrApUuFovvJ8QsdUX0k+3VSs7KyMHnyZERERCAoKAg9evTAoUOHpC5L9iz1pNnyMbamDwobN17AoUOZ2LjxAmJjdxt6JJOThyIuLgJ9+4YgLi5Csg9esXOlD6iVOfr86ZkLf3/9lQuVSj5BNSEhGuHhxr8/qb54iP1OxahUBYiJ2Yn4+L2SncsmTTxF2zUaHeLi9kj+Ppajqn9bzAVUPTl8GSGq78z2pA4fPrzGBxMEAdu3b69TQZXl5eVhyJAh6NmzJzZs2ICAgACoVCoEBgba7DnuVrW5jCqHS6/VXaZWKn1l0bth7nKrGCk+7BISorFz50UUF2uM2ouK1LLqIdJ/8Zg5cx+KihQIDpbu0rS5139Vly4VGgLO0aNZDh2jqu8JVKkKzO5z+7ZatN3Rr0O5DTmw9kuInpRjyomogtmQqtVqIQhCjQ6m05n2JNXFhx9+iODgYKxcudLQ1qJFC5s+x92qNpdR5XDpVQ5B2RrmLreKkerDTqxnF5DfuVQqffH22+0QFRUlaR3mXv+WZGQUYdasI/jqqwftUJExa4cjmOPI16Fchg5VZu2XEEC63nwiMmY2pO7atcuRdZit4f7778eECRNw8OBBBAcH46mnnkJ8fLzZAJ2amurgKuVp3LjGOHr0itH6naGhHhg3rrHZc1Sbx9iat7dGtN3LSyOr362vr3Vf4Bx9/vTmzDmDsjKt6Lbz52/i/vs3IDCwASZPDkezZuKXjh1N6t/vuHGNsW1bGsrKavZl++efsxxS+5w5Z2odUB39OhSrNT09HzNn7sPbb7dzSA1VmfvbUpmXlwv69m2MyZPDUVZ2Damp1xxQmXlSf3EjkpqsJ05dvHgRa9euxXPPPYdp06bh1KlTmDlzJgBg4sSJoo/hm7pCVBSwa1cLJCamICvrdrWXUVNTUzFgQKcaPcYekpKCcO6ccQ+Mh4cCgtAA16974bPPzsri8mHbtpdx+rT5S64uLgL69g3Chx/2l6TGwsJzZrdlZpYiM7MUAHDuXIksJtSkpqZK/t6NigIGD87EN99cMtmmbJaDxJf2oGmTfFy97ouEJUOguhIAAFAoFA6p3dzv1N1dEA3WYWHeUCp9JHkfm6u1qMgx50qM2N+Wqh56KFw2Q2GIqIYhVaPRYPPmzfjpp5+QnZ2NOXPmoEOHDsjLy8O+ffvQq1cvBAcH26w4rVaLrl27Yt68eQCAzp07Iy0tDWvWrDEbUumO2ozflHrMp36M4uzZR7F37xWUlGhQUqLB7t2X8f33GVCr73wYS3n5UGylAUEA9CNetFodLl2S7rK6tZeuOYvZ2IIFvfDdd5eNXmfKZjn4Ye0qRCpvGtp6dlJh8DMToboSgO7dmzikNnO/0549G+Hy5XKTVS+k/PIhh6FDVen/tiQmpuDcuVycOnUTlUeouboKGD++jWT1EZEpq2f337p1Cw888AAmTZqEbdu24fvvv0dOTg4AwMfHB6+//jpWrVpl0+KCgoLQunVro7ZWrVohIyPDps9D8qJU+sLLyw0lJcaX5yoHB0DaGctVVxoICWmAqkOypaxPbNZ8gwYK0X3lNkZVSkqlL9q08TNqS3xpj1FABYBI5U0kvrQHoaFeWLCgl0NqM7cSwvTpkbJZ9UJPTqs2VKb/Et66tb/J+1Wt1uGzz85KUxgRibK6J/XNN9/E2bNnsXHjRnTt2hWRkZGGbQqFAsOHD8f333+PuXPn2qy4nj174vz580Zt58+fR/PmzW32HCRP1k5ykDJgVe51vv/+DYZL6JVJVV/lXiP90I2ionLRS9mcxWysbdtGOH36zs1MmjYRvzzcuX25Q2f2i/1OExKiUVZ2TfIrIFWZq1XqYSV6zjJBk6i+szqk7tq1CxMnTsTgwYNx8+ZNk+0RERH4+uuvbVrcc889hwceeADvvvsuRo0ahZMnT2LVqlWYM2eOTZ+H5Mfay9VyCViBgQ1E26W+vFk5uKhU+fjrrzxZ3AxBzqoO5bh6XTxYtW7XFsX+jg1dYmFU6sk95sgtOFcmx+EIRGTK6sv9eXl5CA8PN7tdp9OhrKzMJkXpdevWDevXr8fWrVvRq1cvvP322/jXv/6FZ5991qbPQ/IjdrnQ1dV4Rr2cAtbkyeGyvLxZmZxuhiBnVc/T0dSJKNUpjfbRKMJR4pMgUYVUV3IdjkBExqzuSQ0LC8OZM2fMbj98+LDREABbGTJkCIYMGWLz45K8iV0uHD++DT777KwsLx82a+Yp68ubenLu3ZKTquepVN0bQkEiXDRZ0CqCUeKTAJ2r0sIRSM4q/31JS8tBy5YBsny/EtV3VofUuLg4fPDBBxg+fDjatm0LAIa1SleuXImdO3di/vz59qmS6iWxQNWnT1OJqqkeA+DdS+eqRLH/aqnLIBvSv1/lsPwZEYmzOqS+/PLLSElJwYgRIxAZGQlBEDBr1izcvHkT165dw7BhwzBp0iR71kpERERE9YTVIdXNzQ0bNmzAxo0bkZycDEEQoFar0blzZ4waNQqPPPJIjW+jSkREREQkpsZ3nIqLi0NcXJw9aiEiIiIiAmDF7P7Nmzdjz549FvfZs2cPtmzZYrOiiIiIiKh+sxhSd+7cifj4eCgU4neq0XN1dcWzzz6L7777zqbFEREREVH9ZDGkrl+/Hr169cLgwYMtHuT+++9Hnz59sG7dOpsWR0RERET1k8WQevz4cavXKP2///s/pKRIc59yIiIiIrq7WAypeXl5CAgIsOpAAQEByM3NrX5HIiIiIqJqWAyp99xzDzIzM606UFZWFu655x6bFEVERERE9ZvFkNqtWzds27bNqgMlJyejW7duNimKiIiIiOo3iyF1/PjxOH36NGbNmgWtViu6j06nw+zZs/Hnn39iwoQJdimSiIiIiOoXi4v5Dx06FOPGjcPKlSuxf/9+jBkzBu3atYO3tzcKCwtx5swZbNq0CefOncOTTz6JBx980FF1ExEREdFdrNo7Ti1btgytWrXCBx98gH//+99Gtz7V6XTw8/PDW2+9hRdeeMGuhRIRERFR/WHVbVFffPFFTJw4EceOHcO5c+dQUFAAHx8ftG7dGj179oSHh4e96yQiIiKiesSqkAoAHh4eGDBgAAYMGGDHcoiIiIiIahBSicj5qVT5SExMQWbmbYSENERCQjSUSl+py5I1nrO7H3/HRPLEkEpUT6hU+YiN3Y309HxDW0pKNpKTh/ID2QyVKh/Dhu1ERkaRoe3o0Szs2hUj+TnTB6u0tBto2fKyUwQrOYbBK1eK8fLLfF8QyZHFJaiI6O6RmJhi9EEMAOnpFaFBKipVPuLj92Ly5BOIj98LlSq/+gc50KxZR4wCKgBkZBRh1qwjElVUQf+FY+PGCzh+/BY2bryA2Njdsjt/lVWu+dChTNnUvGJFuuzeF0RUgSGVnII+zDz79Cc4+e1wKK4MhWduPAS1SurSnEZm5m3R9qws8XZ7c4ag9fPP10XbU1KyHVyJMXNfOIYP3yWr81eZHL8kAUB2dqlou1TvCyK6g5f7ZUBQq+BRkAgXTSa0ihCU+CRA56qUuixJiF0OBIDY2N3QlqXjh7WrEKm8WbFzCaAoT0FRo2RJzlflWr29NUhKCpL15cGQkIai7cHB4u32Zim0rF49yKG1mHvd5eWJBxip6Ovcs+eS6PZLlwoRG7tblpeq5fYlSS8wsIFou1TvCyK6gyFVYoJaBa+bsVBo0isayqUNXlIyN2aybVs/pKfn44tFe+4E1P9RaNLhUZCIYv/Vktd67pz04UClysfs2Ufx668VPYDR0YFYuLA3lEpfJCREIyUl26jm8HBfQyBzNLmEFkuvOzM32kP37k0cVN0dYnWKEQv6Uo8FVanycelSgeg2qcPg5MnhOHeuRDbvCyK6w2xITUpKqvHBBEHAjBkz6lTQ3Uzsg6KNb+KdgPo/UgUvqZnrWbt6tRAA0LSJ+IeziybL7rVVJadeQD2xST67d1/Gb79tQ7dugSgoUEOp9EJJiRq3b5fjnnsaYNmyvpKFarn07Fb3uqtKEIDbt9UYO/ZbFBSoHRb6xOo0p3LQl3rCnP75L10yPZ9yCIPNmnkiOXkoEhNTkJV1G8HB8pjQRUQWQurChQtrfDCGVPOuqk4j7dB0TB6Wg6vXfZGwZAhiY7NxcmcG3EVGBksRvKRmrmettLSiO+vqdfEPDUGjgteNGIcOldDXqmyWg8SX9qBpk3xcve6L7UeetPtzm5OYmGIyyQcArl0rwe7dl03ab90qx9SpByXr/ZVLz251r7uqdDpg//6rRm2OCH3m6hRTOehL/YXKXLgOC/OW/MqDnlLpa3IupO59JiILITU3N9eRddzVBLUK/gWjETvomqGtZycVBj8zESdOuaJvZ9PHaBXBDqxQHsz1rOklLBmCnp1URpf8dXCFQnsJ0F5y6FAJX183KJvlGI+RBdC76yX86zVPTJo6zOEfaDUJMXpS9v4qlb6GHqy0tBy0bBkgSRCo7nVnDUecR3N1KhSARnPn56pBX+phFeaeX6n0kW3ok7r3mYgqcHa/A3gUJCI44JpRW6TyJhJf2oOl/x0JjSLcaJtGEY4SnwRHligLCQnRCA83/wGguhKAwc9MxKbvolGo7QWNSxgEqI320Q+VsDedTofEl0zHyLYMzUGvqFWSzFKvbdiScuKKvgdrxYouWL16kGQ9ul5edR+eb+/zaO79odEAXl6uiI4ORFxchEmQknpYhdTPXxtyXYmAqL5hSHUAF02maHvTwHzArQWKGiWjzCMOare+KPOIq5eTpoA7PWtxcRHo2zcEYWHeJvuorgRgw6F/QdNsN3SKMNHjOGKoREGB2uwY2aaB+ZJ8oCUkRCM01KvGj5NzWHAEpdIXbdv61/k49j6P+veH2PuiqEiN8HBf0aAvFm4dOaxC6uevDal7n4moQo26D86ePYsVK1bg999/x61bt6CtMvVVEAT8/vvvtqzvrqBVhADlpu35tysub+pcfevdJClzKo8NE7vkVvnDzdx5dcRQiZCQhmbHyF7Nrmh39AeaUumLXbtijGb3t2/vj/Pn80XHqgLyDwuOEh7uW6e1TxUKwSHnUan0RViYj+gkJHOvt8rDKqSYGCT189eGM/b+Et2NrA6pP//8M2JjY+Ht7Y1u3brhjz/+QL9+/VBaWopffvkFbdq0QZcuXexYqvMq8UmAojzFaBZ/Vk4QWt/3PprK+A+11Kr7cBM7r44aKpGQEI3nJ442GSN7XtUICUuGAJDmA02p9MWXXw4xatNPAMnKug0fHzfodDoUFqqdIiw4itgkrsoaNWqAnj2DkJNTjJ9/Ng6zggCsWjXAYeexNgFKbGKQI0n9/DUll0l9RPWdkJeXp7Nmx+HDh+Pq1av48ccfodFoEBkZieTkZPTv3x8///wzHnnkEXz66acYNMh5/hA50p0F+7OgVQTLbsH+1NRUREVFSV1GjUl5XlWqfKxctgsxPdbB0/0GMrJ8kLBkCFRXAhAe7stJFjUgh9effo3ZvXuvoKTkzkykqr/Lw4evYsqUA7h1qxT33NMAy5f3R58+TR1ap9gVBr7easfca6/ylzt+oSOShtUhNTQ0FK+99hpeeukl5ObmomXLltiyZQsGDhwIAJg7dy4OHz6MH3/80a4Fk33IISQ4s/37T2L9+hv8QKslOb3+nCGcVK7Ry0uDpKSBsqvRWcjptUdExqy+3C8IAu655x4AQMOGFZeVbt68c5kzMjISa9assXF5RM6hWTNPp7qcSeY5w6XpyjWmpqYyoBLRXcnq2f1hYWFIS0sDADRo0ABKpRL79u0zbD9y5AgaNWpk+wqJiIiIqN6xOqQOHDgQ27Ztg05XMTrg6aefxvr16zFixAgMHz4cX3/9NeLi4uxWKBERERHVH1Zf7n/11VcxZswYqNVquLm5Ydq0adDpdNi6dSsUCgVmzZqF6dOn27NWIiIiIqonrA6pfn5+RktMCYKA6dOnM5gSERERkc3xjlNEREREJDtme1KTkpIgCAJeffVVuLi4ICkpqdqDCYKAGTNm2LRAIiIiIqp/zK6T6u/vD0EQkJWVBXd3d/j7V39va0EQjJalIufBtQLrhuevbnj+ao/nrm54/ojky2xPam5ursWfiYiIiIjshWNSiYiIiEh2GFKJiIiISHbMXu4fPnx4jQ8mCAK2b99ep4KIiIiIiMyGVK1WC0EQanQw/d2oiIiIiIjqwmxI3bVrlyPrICIiIiIy4JhUIiIiIpKdGoVUjUaDDRs2YOrUqXj00Udx+vRpAEBeXh62bt2KrKwsuxRJRERERPWL1SH11q1beOCBBzBp0iRs27YN33//PXJycgAAPj4+eP3117Fq1Sq7FUpEtadS5SM+fi9iYnYiPn4vVKp8qUsiIiKyyOqQ+uabb+Ls2bPYuHEjfv/9d6NJUgqFAsOHD8f3339vlyKJqPZUqnzExu7Gxo0XcOhQJjZuvIDY2N0MqkREJGtWh9Rdu3Zh4sSJGDx4sOis/4iICFy+fNmmxRHJnb6HcvLkE7LtoUxMTEF6unFd6en5SExMkagi8+Te4yuH+lSqfIwd+y2ior5AVNQXeOWVU7I7T0REtmB2dn9VeXl5CA8PN7tdp9OhrKzMJkUROQN9D6U+AB4/fgspKdlITh4KpdJX4uruyMy8LdqelSXeLpWq5xOAJOdTpaoI8JmZtxES0hAJCdFQKn1lUZ9KlY9hw3YiI6PI0JadXYJhw3Zi164YWb3uzJ1HIiJrWR1Sw8LCcObMGbPbDx8+jMjISJsURSRn+g/f/fuvIDu7BMpmOUh8aQ+aNsnH1eu+WPxOKT5Y9pTUZRqEhDQUbQ8OFm+XiqUe39WrB9n9+VWqfMyadQT79l1FSYnG0K4PolLXB1Sco8oBVS8jowizZx+Fl5ebLEKhHAI9ETk/q0NqXFwcPvjgAwwfPhxt27YFAMNl/5UrV2Lnzp2YP3++far8n/feew9vv/024uPj8c4779j1uepCUKvgUZAIF00mtIoQlPgkQOeqlLossoGqH77KZjn4Ye0qRCpvGvbp2VmFaVOBl1+LlcUHckJCNFJSso0CQ3i4LxISoiWrqWov27hxjSXt8RULVXrp6fno1WszIiPFf5eO7JE2d44AYO/eK6LhWorXoBwCfU2w15dInqwOqS+//DJSUlIwYsQIREZGQhAEzJo1Czdv3sS1a9cwbNgwTJo0yW6F/vrrr1i3bh3at29vt+ewBUGtgtfNWCg06RUN5YCiPAVFjZIZVK2kUuVj9uyj+PXX6wCAhx7QYvHsffDxuCF56K/64Zv40h6jgAoAkWE3cX+nTxEb20AWPUdKpa+hJzAr6zaCgxsaAmp8/F6HfzCLBcKjR6+gU6cmovvbq8e3cjC5dKkAly4Vmt339m01Tp26Kbrt+PFsHD58FX36NLVLnZWZ6xUHYBRQAWlDobMMMQGAK1eK8fLL7PUlkiOrJ065ublhw4YNWLFiBSIjI9GqVSuo1Wp07twZK1aswBdffFHj26ha69atW4iPj8fSpUvh5+dnl+ewFY+CxDsB9X8UmnR4FCRKVJE4Qa2CZ248vG7EwDM3Hu7CFalLAnBnzN0331xCdnYJGrpfQcKTb8JfkQzX8kNwL9kIr5uxENQqSeqr+uHbtIn4hJWmgfmynJykX5QjI6NQshn/Yr1sGRkl0Ol0CA83DgX26vHVv870/35LAVVPpwMUCtO/cbdvq/Hww9/g8OGrNq+zqoSEaISGepm0N2gg/qdcqlDoLENMAGDFinSnmVhIVN9Y3ZOqFxcXh7i4OHvUYta0adPw8MMPo3///li0aJFDn7umXDSZZtrlcaMDQa2Cx61ZcCvbBwElFY3lQCvPoyhT75K8t7fqmDuxnkqFJh1//DAV/1o2yeGX5qp++F69Lv68V7Mr2qUICVUvXY4f3wZTpx40+iDevPkCtFrjxzmq581cL1thoVq0x9cev9tZs46Iju2sTmjwDSyY/h2CAm7h6nVfJCwZAtWVAKjVOkyZcgAnT461ea2VKZW+2LUrBrNmHcGxY9dw+7YaHh4uaNjQXfS8+vi42bUec8aPb4OtW9OgVt9ZqtDVVcD48W0kqceSy5edp9eXqL6pcUh1tHXr1iEtLQ0rV660av/U1FQ7V2RZeANvBIh8Lty67YV0iWtzF66gledUuLtkmGzzcMlA0dWZSC99W4LK7khLu2H0s7meyvLiqzh0qOILwdGjV7BsWWc0a+Zp9/rGjWuMo0evICOjIuAnLBmCnp1URkH6vKoREpYMAQB4eWkc+pq8cqUYU6f+YagPAHbuTEdxsXEirRpQ9dLScuxer7e3RrTdy0uDsrJrmDGjuaGtrOwaUlOv2byGn3+u+ZdG0fHHnVQY/MxEqK4E4ObNYof9ridNaopTp7KRm6tFaakWt26poVAAmiqn9vjxLOzff9Ih743Kli49YxRQAUCt1mHp0l/RpEk7h9ZiyZUrxbhwQTyMCkKZ5J8nUVFRkj4/kdRqFFL379+PdevW4eLFi8jNzTVa0B+omEj1+++/26y41NRUvPXWW9i9ezfc3d2teozUb2pBnQTNzXNGl/w1inC4BSYhSuJeSs/cRXAvMQ2oevc0LEJUmLTnr2XLyzh+/Jbh5+p6KoGKS8Xr199wyNi7qChg164Wht4+b+/mmLN6DmLv+wKB/sa9a+HhvkhKGujQcW2LFu01CqgATAKqJS1bBtj9PZSUFIRz54zHAIaGejj0XCkUxwCUm7S7uJgP8KLjj5U3kfjSHjw543E0auTpsL8/Yr/nqgEVAK5dK3PYe6OywsJzou1FRQrJ/0ZXtmjRXpSUiP/CvbwayqpWovrI6pC6fPlyvP7662jcuDGio6MNM/zt6ZdffkFOTg569eplaNNoNDhy5Ag++eQTXL16FQ0aNLB7HTWhc1WiqFHy/2b3Z0GrCJbN7H5zQxH0tIpgB1ViXkJCNI4ezTJciq2up1LPkZfmlEpfkw/91NT74O4ehBWJKQhreRv/6C3NDGFLs7+r4+GhcMiMf7GJXOPGNXbouerevQm++eaSSXu/fk1x/vwt0aEAlsYfu7oKWL68v83rNKcmv2cpLls7y5hUS+exsFDtwEqISIzVIfWjjz5Cnz59sHnzZqt7Netq2LBh6Nq1q1Hb888/j4iICEyfPt1hddSUzlWJYv/VUpdhQqsIEes8AgCUaENR5pPg2IJE6MfczZ59FFmXz2D2sz+gTNcIpdqGUCMQO/YImPXeA1BdCTB6nBw+/MTCq6OZCwdeXq4oKrL8oTtwYFOHBcWq58rRl1UXLOiFkydzjMJoaKgXlizpCwAYMGArcnONb05irlf/VlEjbNv2kENm9+tZmuVflRTvDTkueybG0nmUw98UovpOyMvL01W/GxASEoL58+djwoQJ9q7JomHDhqFdu3ayXidVrkyWxwKggwfKGwzC2ZsToYwcIF1xVYjVmpUThJ6PTjAJqF5erjhyZLSky8WkpqbK4tKg2PJO4eG+WLasLz766JTJWpqV95FyyR0pzp9+gpnYJK34+L3YuPGC0f7KZjk48t9P0bTxnTGyGkW4JMvLif2e9bP+KwdvKX+vls6vXKhU+RgyJBlZWaVG7aGhXrK7gxdRfWR1T2qXLl1w6ZLp5TFyHpaGIpTlSDtBoCqxpbyCA64Zxv9V1ratPz9M/sfcmqhKpS/69GlqCA4XLxbg2rXbaNLE09DDVd/OoaWeb7GeQBf3cNzy3YzGHkskH8pT+feclpaDli0DDL2UcgmGcriyUB2l0hcrVnTBqlWZhnWZo6MDsXBh73r3fiCSI6t7Un/77TeMHTsWq1evRr9+/exdFzmYXHoC9bxuxMC1/JBJ+95jEbh/wmSjtri4CMk/DOV2/pyNHM+fM/QEAvI8d86E549Ivsz2pIqtherr64vY2FhERESgefPmUCgURtsFQcCGDRtsXyXVO+bGz1ae1Q/Ic5wb3R2coSeQiOhuZjaknj17VvQOUqGhoSgtLcX58+ftWhjVbyU+CVCUpxhd8q86qz8szJu3LiQiIrpLmQ2pp06dcmQdREYqj589deJP/HW+gWH9UT2l0ocBlYiI6C4lfsNnEYcPH8aNGzfMbs/JycHhw4dtUhQRcGcpr6SvEvHkjMdluewUERER2YfVIXX48OHYt2+f2e0HDhzA8OHDbVIUUWUJCdEID+dYVCIiovrE6iWoqt4CtaqysjK4uFideYmsZmlZJSIiIro7WQyp+fn5uHXrzn3Ub968icuXL5vsl5eXh82bNyMkJMT2FRKBM62JiIjqG4sh9eOPP8aiRYsAVCwvNXv2bMyePVt0X51Ohzlz5ti+QiIiIiKqdyyG1AEDBsDDwwM6nQ5vvfUWRo0ahY4dOxrtIwgCGjZsiK5duyI6mmMEiYiIiKjuLIbUnj17omfPngCA0tJSDB8+HO3bt3dIYURERERUf1k9cWrWrFn2rIOIiIiIyMBsSP3qq68AAI899hgEQTD8XJ2xY8fapjIiIiIiqrfMhtTnnnsOgiBg9OjRcHd3x3PPPVftwQRBYEglIiIiojozG1L/+OMPAIC7u7vRz0RERERE9mY2pIaFhVn8maonqFXwKEiEiyYTWkUISnwSoHNVSl0WERERkexZPXGqstOnTxsW9W/evDnat28PQRBsWpizE9QqeN2MhUKTXtFQDijKU1DUKNmpgiqDNhEREUmhRiF18+bNmDdvHq5evWrU3rRpU8ybNw9xcXE2Lc4ZmAtxHgWJdwLq/yg06fAoSESx/2qJqq2ZuyVoE9WESpWPxMQUZGbeRkgIb8FLRCQVq0Pq+vXrMXXqVERFReHNN99EZGQkdDodLly4gM8//xyTJk1CWVkZxo0bZ896ZcVSiHPRZIo+xkWT5cAK6+ZuCNrkPOQQDlWqfMTG7kZ6er6hbceOixg4sCkWLuzNsEpE5EBWh9T3338f9957L3bu3AkPDw+jbfHx8XjooYfw/vvv16uQainEaRUhQLnpY7SKYAdVV3dSB205hBayP5UqH6+8chK//HILJSUaQ3tKSjaSk4c69HeemJhiFFABoKREg927L+Ps2d0Or4eIqD5zsXbHK1euIC4uziSgAoCHhwceffRRk2EAdztLIa7EJwEaRbhRu0YRjhKfBEeUZhVBrYJnbjy8bsQgvMEcCGqV0Xati/iHsdbFx241qVT5iI/fi8GDk9G792Zs3HgBhw5lYuPGC+jRYxPGjv0WKlV+9QdysCtXihEfvxcxMTsRH79XljXKkb7n8qefbhoFVABIT6/4kuJImZm3zW6Toh4iovrM6p7UNm3aIDNTPJQBwNWrV9G6dWubFOUstIJ4WNMqgqFzVaKoUfL/xqtmQatzgUKbCu/svtC5+OH2Pcuh9ejj4IrvqDpUIcAN0GV/B53gB7V7T5T4LgB0OvEHm2uvI7FLrZVJ2aNlaQKZSpWPqVP/QEZGiWF/KXoBnZFYz2VlWVnmQ6M9hIQ0tLjd0fXUFK8+ENHdxOqQ+tZbb+Hpp59G586dMXLkSKNtmzdvxueff47PP//c5gXKlaBWQaE+ZdKuEUINvaU6VyWK/VfDpeQwvHNHQMD/eoq0+fDOHYFC/+2SBVWPW7NMhioI0ELQ3YR76TdQ5JyETggSfayLrtDm9ahU+Rg+fBcuXTJ/bGWzHCS+tAdNm+TjxqnP0aLZxw6ZwFXdBLLExBSjgArc6XVbvXqQ3etzZpYCKgAEB1sOjbakUuWjsLAMLi6AViu+j7d3rRZEqRNrg6fYlzw5fVlSqfIxa9YRpKRkAwC6d2+CBQt6yaI2IpInIS8vz6pusbi4OKSnpyMtLQ2BgYEIDw+HIAhIS0tDdnY2IiIi0KJFC+ODCwI2bNhgj7ol55kbD/eSjSbtWqER1A3uN+pp877WCgrtdZN9NS5NURh0xu61VlURmodDgJlP4v/RuIRBob1k0l7mEWfTiVPV9aACFQH1h7WrEKm8aWgr1SlR2mS73YOqud/1d8d6Y8nGl3DsWBZu3iwz2d63bwh27Iixa23OrlOnr8x+MQkP93VYwFKp8jFs2E5kZBRZ3C801AsrVw7AZ5+ddUhvpdh7o+p5SU1NRVRUFOLj92Ljxgsmx4iLi5D8y5K58xsa6oVdu2Ic9juePfsofv214m9xdHQgFi7sjbKya4iKirL78xNRzVndLXD27FkIgoDQ0FAAMIw/bdCgAUJDQ1FaWopz584ZPeZuXjvV7HhU3U24l2w09LQBgItIQLXUbk+CWgWv3DHVBlQA0Al+0CgURj2u9hhXW90lXwBIfGmPUUAFgAaCCoIDVhow97t2xTV8841piNdzZC+gswoM9BQNqY0aNXBoD+CsWUeqDagAkJFRhEce2YOiIrWhzZ69lWLvDXO99ObG08phiELF1QbT85uRUeSQKw5iIXn37ss4dWonli3rAGZUInmyOqSeOmV6abs+Mzd7X08/yx8AzEV1HRS2L0xE5fGUgiYNLii27nG6PBQF7LgzrlYRbJfF/Kt+uOov67cMzUFwYAGysr3Rsnmu6GMdsdKAud/11WzzoSQ83BcJCdF2rMo6ch6jKKhVWPzaWpSXXMXV675IWDIEqisBAID77w91aJ36S9DWqBxQAfsO7ahJ8DQ3nlYOX5YsTUhzRIi2FJJXrEjHgAGd7F4DEdWc4wdY3SVKfBKgKE8xGddZWUWAsjSaogE8c+Ptehcnk/GUNaATmhjG1dpT5Q9Xscv6LUPFAyrgmCW9xH7X51WNkLBkiOj+7u4ukowDrBpIx49vg0mT9ht9OB89muWwy6uW6F+XfTvfOac9O6kw+JmJcHEPl0XArwl7Ba2aBM+EhGikpGSbDA2Qw7m0NCHNESHaUkjOzjYdqkNE8mBxCao1a9YgLS3N8LNWq8XZs2dRXGzaE3fixAnMmDHD9hXKlH72fplHHLRCoOg+gkZldhknAHBBPtxLNsLrZqzJ8k+2IraWq7W0buHV72QDCQnRCA+vOE9il/XNuV3iARd1Ojxz4+12/oA7v+uDf/TF3mMR+M+Orhj8zERDr19VanX1QylsTT92sfKSXWPG7DHpPcrIKMLs2UcdXl9VYq/LSOVNfPHeYUkCfvfuTazaz8tL/Hu9vYJW5feGnrngqVRWjFWNi4tA374hiIuLkM2kqYSEaISGepm0h4Z6OSREWwrJgYHudn9+IqodixOnGjVqhJUrVxpud3rz5k1ERkZi69at6N+/v9G+GzZswOTJk3HzpnUB425iqbdSI4QCAqDQZlg8hq0nI+l53YiBa/mhGj9Oowi3++1PK/f8+fi44o8/cvDF/PcxqIfp5A+9rGxvpF32R6c21+HdsNSh9cbE7MShQ+aXYavM0ZNVzE2aERMY6IHU1CftXJFl5l6Xare+KGq8w+H1WDNxysVFwOrVA5CYeNziRCZ71JaYmIKsrNsIDjYdsqGfOCV3Us7utzRxa9myDrzcTyRTFi/360TWwxRrq+/0PW1eOcNNZsMrdBkocxsKjUsvuGiy4KI+Cxed6fg3e42trG7sbGUalzDoFEq7jT2tTGzWcmioF/IKGwEwH7ZO/N0B3t5u8G542ajdEbdrrW4NzcocPVnF0uVMOZLbHdmUSl+sXDkADz/8DdRq8b9xWq0OiYnHsWxZX3z22VmzodEetUk9O98WlEpffPXVg5I9965dMWZn9xORPHFMqo3oXJXQKcIAkSWbXHSFKPL/CoCFpavs9OEsNp5SgyC4IB9CpQlUJdpQlAXucMi6o4D4rOWMjCJsP/oEene5hOAA0w+OUp0SfWJXomHe86IBx96TqMTG/Hl6KlBcrDHZ19GTVWoSoKOjxYenOJLo61LiO7J99tlZswFVLz09H599dvauCI31jVLpiy+/NB1HnprKkEokV1bfFpWqp1WEmGm/E0AdfbvUymNn1W59UeYRh6LA71AQeMyo7e/iZQ4LqID5nr+0SwFo2Oa7itpcu0PjEga1IhplHnGGNVGtOc/2IDbmb9OmB60eM2hPYmMXQ0O9EBTkYdK2cGFvR5YmqurrMqf8QbsP16iOtb3RcljSiYioPmBPqg1Z0ztkcrtUB1xaNzdDv3Jb2Y1Uuz2/GKtmLQsNoHHvYXJ+pOyFE7v0mpw8FDNn7kNRkcIhl3/N1ZWcPNRk7CIAi+MZpVT5dZmemoooCQMqYH1vtByWdCIiqg+qDakpKSlwda3YraCgAIIg4PDhwyYTpH799Vf7VOhErA2gjljWSe7MLZfzZkITi7cgBaQJ+pYolb54++12kk9eMTd2kZemrSP2mnR1FYyGAMhlSSciovrA4ux+f3//mh1MEOrl7P67gRQzhMVmLbfxfUV0zK69Vj+wFWeZYS1Xcjl/VV+T48e3cegkqdqQy7lzVjx/RPJlsSd1xw7HLwVD9YdYz5/LDTO3m3XAnaWIxF6Tffo0lagaIqL6zWJIve+++xxVBxEA+S1NRERERNLg7H6SFUevfkBERETyxNn9JCtymxRFRERE0mBIJdnh6gdERETEy/1EREREJDsMqUREREQkOwypRERERCQ7NQqp+fn5ePfddzFixAj07t0bKSkpAICbN29iyZIluHDhgl2KJCIiIqL6xeqJU1evXsVDDz2EK1euICIiAn///TeKiooAAI0aNcLnn3+Oq1evIikpyW7FEhEREVH9YHVIfeONN5Cfn48DBw4gKCgIkZGRRtuHDRuG7777zuYFEhEREVH9Y/Xl/h9++AGTJk1Cu3btIAiCyfYWLVrg6tWrNi2OiIiIiOonq3tSb9++jaCgIIvbtVqtTYq6mwhq1f8Wps+EVhHChemrwfNFREREQA1CakREBI4fP47x48eLbv/hhx/Qrl07W9V1VxDUKnjdjIVCk17RUA4oylNQ1ChZ0uAlFgTlQK7ny9moVPlITExBZuZthIQ0REJCNJRKX6nLIiIiqhGrQ+rTTz+N119/HX369MHgwYMBAIIgoKioCAsXLsRPP/2E5cuX261QZ+RRkHgncP2PQpMOj1uzUBzwlSQ1mQuC7sJiAFGS9mSaPV95LwGKQJOa2OtqSqXKR2zsbqSn5xvaUlKykZw8lEGViIicitUhdeLEifjrr78wZcoU+Pj4AAD++c9/Ii8vDxqNBpMmTcKjjz5qt0KdiaBWwSN/NtxKd4tudyvbjdKSw9B69HF4XV45w6HQXjJqV2jS0d5zDIQsXwi62xBQUrHBwT2ZLppM0Xa38v0QynGnprKDuH3PWjTMn2oUtl1Lv0GR3waHn1c5SUxMMQqoAJCeXtGzunr1IImqIiIiqjmrQyoALF68GI899hi2bt2KtLQ0aLVahIeHY9SoUejVq5e9anQqFUFwGBTaDPP7APDKHQYBrtBBAbVrT5T4f2jXIGjoQa0SUPUULmpAd9O0XZMOj4JEFPuvtltteloX8Z6+qtP0FNoseOUOM5n156IrgnfuIygIPFJve1TT0vJF27Oybju4EiIiorqpUUgFgB49eqBHjx72qMXpVQTUB6HQivcIVlYRsNQQoIa7+gDcsruj0H+rXXoBa1KXGJfy9Op3soXyG1bvam5ZCgFFDgvVcqNS5ePs2VzRbcHBDR1cjfxxuAgRkbzVOKSSMcMHXXkaFJpTEFBWu+OgDF55j6Cwcd16Aat+8JZ6jkfDW5NqHVABQNBdr/VjreVSchhu2l9scyxNlk2OU1VNQ42jJzAlJqagqEht0u7l5YqEhOha/RvuVpykR0Qkf2ZD6vDhw2t8MEEQsH379joVVNn777+PHTt24Pz583B3d0d0dDTmzZsnm1UETD7o6shFV7deQLEPXtfSb+CiK6pTXYIuH4JaBQB2CTiCWgXv3DEml/VrS+viY6Mj3VHTUCPFBKbMTPFL+i4uAhITU/BmQhO08nzS6N/gVvINCv2lH8d75UoxFi3a67BAb3aSXkEizua/x9URiIhkwGxI1Wq1oov2W6LT6epcUGWHDh3CM888g27dukGn02H+/PmIjY3Fzz//DH9/f5s+V22IfdDVlWvJbnjmxtcqAIrVU9eAWnGMPPhk94AW90CBaxWNNux58ihIhIDiOteppyg9DkGtsmmPWHWhZs6cMygsPGcINVJMYAoJEb+kX1BQjo0bL+DxAQvRdpDxv0FAkU168OtCpcrH1Kl/ICOjxNBm70BvbpJe2e0M0S8Xy5b1xWefnWVwJSJyILMhddeuXY6sQ9SWLVuMfl65ciXCwsJw7NgxDB06VKKq7jD3QVenY6IQ7iUboSg7iqKAXTUKDvaoR09ACRQoMWqz1aQqF7Vtg74C12xSV+XL9ctn/4UOLU33MRdqAgIaiB7TnhOYEhKikZKSbahF2SwHiS/tQdMm+bh63RdN/HNEH1fXHvy6SkxMMQqogP0DvVYRApSbtn+/Ty365eKRR/YYDaXgsl5ERPbnVGNSCwsLodVq4efnJ3UpAMx/0NmCQpsBj/zZKG70ZZ3r0cF0hryt2GL8p6C1/ZjXutZV9XL973+6iYbUU3+W4a0pKwxBMGHJEKSnAxqNt+hx7TmBSan0RXLyUCQmpuDsqd+w5YNViFTeWbEhv9Dd7GPtNY7XGuaGKdgz0Jf4JEBRnmLUO37xaiBeXnC/6P5Vx/pyWS8iIvuzOqRevnzZ4nZBEODh4YGAgIAaDxOw1qxZs9CxY0f84x//MLtPamqqXZ5bjLswDq08j8LDxfxyU3UhFB+r0b9HrJ4SbSgaCBl2S6m3bnshvY7nvLWHD3xs/HWprnXNmXPGqEdtxX974JEH/4C7251b/5aXC2geeA69OhYa2np2UmHwMxPh7eOD0FAPox7C0FAPjBvX2O6v0RkzmiP/7DtGARUAfL3LUF7uAjc309sXZ95ogGu5jnvvVObtrRFt9/LS2PVcuQuL0cx9BdyEbKT87o5/zuoPAPhi0ZdGXzpUVwJEH5+WluPQvzeWyKUOZyXX8xcVFSV1CUSSsjoadOrUyarw6eHhgT59+mDGjBno3r17nYqr7F//+heOHTuGb7/9FgqFwux+jn1TR6FMvQvu2QPgAvGlf+pCoVDU8N9TUY9LQSJcNFnQKoJR5pMA9+zutV51wBKNIhxugUmIquNYxga57YCSP21UFaBBENya1q2uwsJzRj9Pfuxno4AKAG5uOoQGFxq1RSpvIvGlPdj+6xzD2NSsrNsIDnbsOEaFmQ7bk+eaIKrFTfh633k9nFc1woR5A/DRqiBJLl8nJQXh9OltRoE+PNwXSUkD7VxPFIAB0AGYN2UngNP4Ya1x73PPTiqMmDoFf533M3l0y5YBsggRqampsqjDWfH8EcmX1SF16dKlWLVqFS5fvowxY8YgMjISOp0OFy5cwKZNm6BUKvH444/jwoUL2LBhA2JiYpCcnGyTRf5nz56NLVu2YMeOHWjRokWdj2dLOlcldC4+gNb2IVXtFl2reqqOLVS7dIG7jZZ30rg0hU4RAa0i2Gaz+0t8EuBWstFmnb2aBvfWua6qk5CaNhFfJF9My+a3kTCkIpBKdTnYvWEoqgwhBgD8lR6C0dPGV4xVDczH1Wx9b2EDyS5fK5W+WLasM9avvyFJoAcqft+TRuwx6X2OVN7E91/+jr6PjjDqWQ8P9zUs60VERPZhdUi9efMmiouL8dtvv5nMrJ81axaGDBmC0tJSJCUl4bXXXkP//v2xcOFCbNu2rU4Fzpw5E1u2bMHOnTvRqlWrOh3LXnQuTQAzd3KqLY0QipJ7FtrmYG6NgVLbHEqniEBR4x22OZj+mK5KAG6w1QBfF21BnY9RdRLS1evWB6a2HdvCJVTaCTViYy7PqxoZLl8/OeNxk8dIeVeqZs08JR3fmZAQjaK/xFfCCGqUbxjrK1WIJiKqj8zduMfE6tWr8dRTT4ku/RQQEICnnnoKq1dX9OA1btwYTzzxBE6cOFGn4l599VV8+eWXWLNmDfz8/HDt2jVcu3YNhYWF1T/YgbSu4XU+hg4CNC5NoXbtjjKPOBQ1rtnMfktctNb3AlZHqwi22bEqK3e33TqdtqhRPwkpLi4CffuG4GjqRBSVNzfa5+IVP1y+Zvx+0CjCoQh+s87PX1c6VyWKGiWjzCMOare+yNXEYvHmfyOsZQeEhTl+UpfcKZW+aNNBfP1lrSLY0Cu+Y0cMVq8exIBKROQAVvekZmdnQ602vZuNnlqtxvXrd2ZpN23a1OL+1lizZg0A4OGHHzZqnzlzJmbPnl2nY9uSWK9VTejggUL/zXZbUN1WqxBo4YkSn4S6H0hEyT1LoMgZAoW2brPMNYpwm9VY9XK9Rt0buVnzkKE6j8zrvth25ElMndoRZR5LUFKYBg/vlrK6g1PloR8uAOa/U9EudqMBXr4GFMFvQnPzD6P3sS1fT0REVDNWh9T27dtj7dq1eOSRR9CsWTOjbRkZGfjkk0/QoUMHQ1tqaiqaNGlSp+Ly8vLq9HhH0fdaeeTPhlvpdxBgXTjXASh37YES/1V2DTZiIbq6Zal0aACh0hgBHTxR5L/JbnXqXJUoCtgDz+v3w024UaPHalzCoFMobTpO1lyNLqGfISwUCAPQY2RFezFWI/VGKqKaO8fki8pLVfHy9R2G93GliYdy+tJBRFTfWB1SExMTMXr0aERHR2Po0KFo2bJi0ci0tDTs3r0bOp3OcLm/pKQEGzZswJAhQ+xTtQzpXJUobvQlStQqeN0YBIVOfOF0HQAdGkLn0hi371nukNtRin34lnqOR4Piz+BSng6F5i8IuDMeT6MIx23fZRXbHfhhrXNVQuc5ECjZaPVjNIpw3m+9FqSc1CVnYhMPiYhIGlaH1F69emHPnj2YP38+vv32WxQXV9zG0tPTEwMHDsTs2bPRsWNHABXLUP3999/2qVjmdK5KFDXeC6+cYVBoTddPFQCUewxz+Aeh2Idv8f8CsqBWofzqTNzTsMgokBZLcD/3Ep8EKMqOip67ynRogHL3QSi5ZyEDKhER0V2oRkuod+zYEV999RW0Wi2ys7MBAIGBgXBxsXr+Vb1Qcel6F7xvDIaLLttku5R39xGjc1UivfRtRIVJf7laf+488mfDtewYBF0eBNxZn1QHD5Q3GIQS3wUMp0RERHexWt3nx8XFBUFBQbau5a6ic1VC3WAA3EUuXdtrhvzdQj90Aqjo5eUYQSIiovqnRiE1Ly8PmzdvxsWLF5GbmwudTme0XRAELFu2zKYFOjOxCUucLVwzHCNIRERUP1kdUg8cOIAnn3wSBQUF8PHxgZ+fn8k+1tw2tT7hbGEiIiKi2rE6pP7rX/+Cv78/du3aZZggRdVjTyARERFRzVk94+n8+fOYMmUKAyoRERER2Z3VIVWpVKKkpMSetRARERERAahBSJ0+fTo+/fRT5Obm2rMeIiIiIiLrx6Reu3YNjRo1Qrdu3TBy5EiEhoZCoVAY7SMIAl588UWbF0lERERE9YvVIfWNN94w/P+nn34qug9DKhERERHZgtUh9Y8//rBnHUREREREBlaH1LCwMHvWQURERERkYPXEKSIiIiIiRzHbkxoTEwMXFxds2bIFrq6uGD58eLUHEwQB27dvt2mBRERERFT/mA2pOp0OWq3W8LNWq632tqc6nc52lRERERFRvWU2pO7atcviz+TcBLUKHgWJcClPg6DLRhtPX7jntkWJTwJ0rkqpyyMiIqJ6zuqJU3T3ENQqeN2MhUKTbmjzVgAoOQ1FeQqKGiXLMqgagrUmE1pFCAM1ERHRXazWIfXgwYPYsGEDsrKy0KpVK0yePBnNmze3ZW1kQ5UDnqC5BIX2kuh+Ck06PAoSUey/2sEV3iEWRl1KU9AwfyJcoKnYqRyyDtR0d+EXJCIix7MYUhcuXIj33nsPp0+fRlBQkKF9/fr1eOGFFwxjUH/44Qds2LABP/74I5eqqkIOH25iPaeWuJbshve1TtC5NIHWNdyhNbuUHIZX3iNw0RVVNJQDbiXbAJSh6ohoOQRquvuZvH/4BYmIyCEsLkF18OBBDBo0yCiglpaWYvbs2fD19cW2bduQkZGBTz75BIWFhXj//fftXrAzcSk5DJ/sHnAv2QjX8kNwL9kIrxvDIKhVDq3DoyDR6oAKAC4ohEJ7Ca7qlIqab8Y6pGZBrYJ3bqWAqm8XCaiGWjVZdq+L6jex94/+CxIREdmPxZCalpaG6Ohoo7YDBw6goKAAU6dORb9+/eDl5YWRI0fikUcewf79++1Zq6wIahU8c+PhdSMGnrnxhhBnaM8eDK/cGAgoMXqcQpcBj1uzHFqri9r6gCpGoUmH943BRv9Oe/AoSISAoup3rESrCLZTNUQVXDSZZtr5BYmIyJ4sXu7Pzc1FcLBxCDh48CAEQcCQIUOM2rt06YKvv/7a9hXKkLnLf7d9l6Fh/tRqey1dy36AZ248Sj3Ho0HxZ3YfCiBor9f5GC66bLiXbLTrZU5zYcAcLRQo8UmweR1ElWkVIUC5WDu/IBER2ZPFntQmTZrg6tWrRm1Hjx6Ft7c3OnToYHwgFxe4u7vbvkIZMnf5r+GtKVZdVndBOdxLNsI7d7jxUAA7XVbXCYE2O5Y9L3NqFSFW76uDgNu+qwxh2VzPNlFdlfgkQKMIN2rTCl5wUafztUZEZEcWQ2q3bt3w5ZdfIi8vDwBw+vRpnDhxAv369TNZ2P/cuXNo1qyZ3QqVE3M9foL2Vo2OI0Br9LO9AqDWraVNj2evy5wlPgnQCl4W99EB0Lg0RaH/Tmi8RgO407PtiMBP9Y/OVYmiRsko84iDWhENHbzgoity+JhtIqL6xmJIfe2115CVlYVu3brhoYcewkMPPQRBEPDSSy8Z7afT6bBz50706NHDrsXKhbkeP53LPXU+tq0DoKBWAboi6NDAZse012VOnasSWkVbi/uUuw1AYdAZaD36GNo4sYXsTeeqRLH/amjdwk3GTfO1RkRkHxZDavv27bFt2zZER0fjxo0b+Mc//oEtW7age/fuRvsdPHgQ3t7eGDFihF2LlQuxy38aRThu37O8zmHQlgHQ0MNY+g0ElFYcX1vNg6qhFbzsOg5U6xpueQeXhqZNnNhCDsLXGhGR41S7mH/Pnj2xYcMGi/v069cPR44csVlRcqe//Fex/mkWtIpgw6Sn8gb3w730m1odV6MIt2kAFOthdHEBLmX6ItC/CJ4eGouP18HFaEiCDl4o8ttg17UhS3wSoChPMTu210VbYNLGiS3kKHytERE5jsWeVDJPf/mvqPEOFPuvNgS3Et8F0MHyuErDMdAAZe5DoXbrizKPOJvPmjfX63NeFYi2Ma/hYoavxceXu1bUpa+vIPCI0WV2e9B/AdC4iN8UQiwMmOvZ5sx/sjW+1oiIHKfWt0UlcTpXJQr9NxjfNQkVE34qTzXTwhNF/pvsGvrM9fq4eTZFWMsOeGdDEua/tAU+rscBbS5cBJ1hH40QihL/DyW5o47OVYmigB0md8kyFwYs9WwT2RJfa0REjiPk5eXpqt+NaurO7VArPsjurInquA82sduhahThoj22qvP70SZgvaw+eKueQznUZE5qaiqioqKkLsNp8fzVHs9d3fD8EckXe1LtRD8coLJiO18qF6vB2l6fMl0zk3qlJnYOiYiIqH5gSL3LMegRERGRM+LEKSIiIiKSHYZUIiIiIpIdhlQiIiIikh2GVCIiIiKSHYZUIiIiIpIdhlQiIiIikh2GVCIiIiKSHYZUIiIiIpIdhlQiIiIikh2GVCIiIiKSHYZUIiIiIpIdhlQiIiIikh2GVCIiIiKSHYZUIiIiIpIdhlQiIiIikh2GVCIiIiKSHYZUIiIiIpIdhlQiIiIikh2GVCIiIiKSHacIqWvWrEGnTp0QFBSE/v3748iRI1KXRERERER2JPuQumXLFsyaNQuvvPIKfvrpJ/zjH/9AXFwcLl++LHVpRERERGQnQl5enk7qIiy5//770b59e3z44YeGtm7duuHhhx/GvHnzJKyMiIiIiOxF1j2pZWVl+P333zFo0CCj9kGDBuHnn3+WqCoiIiIisjdZh9ScnBxoNBoEBgYatQcGBuL69esSVUVERERE9ibrkKonCILRzzqdzqSNiIiIiO4esg6pAQEBUCgUJr2mN27cMOldJSIiIqK7h6xDqru7O7p06YJ9+/YZte/btw89evSQqCoiIiIisjdXqQuozvPPP49Jkybh3nvvRY8ePfDJJ58gKysLEyZMkLo0IiIiIrITWfekAsCoUaOwYMECvPPOO+jbty+OHTuGDRs2ICwszLAPF/uvnffffx8DBw5E8+bNERERgUcffRRnzpyRuiyn9N5778HPzw+vvfaa1KU4jaysLEyePBkREREICgpCjx49cOjQIanLcgoajQaJiYmGv3udOnVCYmIi1Gq11KXJ0uHDh/HYY4+hbdu28PPzw/r1642263Q6LFiwAG3atEFwcDCGDRuGv/76S6JqiUhP9iEVAJ599lmcOnUK169fx4EDB9CnTx/DNi72X3uHDh3CM888gz179mD79u1wdXVFbGwscnNzpS7Nqfz6669Yt24d2rdvL3UpTiMvLw9DhgyBTqfDhg0b8PPPP2PRokUca26lDz74AGvWrEFSUhJ++eUXLFy4EKtXr8b7778vdWmyVFRUhHbt2mHhwoXw9PQ02b5kyRJ89NFHSEpKwt69exEYGIiRI0eioKBAgmqJSE/2i/lXh4v9205hYSHCwsKwfv16DB06VOpynMKtW7fQv39/LFmyBIsWLUK7du3wzjvvSF2W7L311ls4fPgw9uzZI3UpTunRRx+Fv78/VqxYYWibPHkycnNz8fXXX0tYmfw1a9YMixYtwrhx4wBU9KK2adMG8fHxePXVVwEAxcXFiIqKwttvv82hZUQScoqeVHO42L9tFRYWQqvVws/PT+pSnMa0adPw8MMPo3///lKX4lR27dqFe++9FxMmTEBkZCTuu+8+rFq1CjqdU39ndpiePXvi0KFD+PvvvwEAZ8+excGDB/F///d/ElfmfFQqFa5du2b0OeLp6YnevXvzc4RIYrKfOGUJF/u3rVmzZqFjx474xz/+IXUpTmHdunVIS0vDypUrpS7F6Vy8eBFr167Fc889h2nTpuHUqVOYOXMmAGDixIkSVyd/06ZNQ2FhIXr06AGFQgG1Wo1XX30Vzz77rNSlOZ1r164BgOjnSGZmphQlEdH/OHVI1eNi/3X3r3/9C8eOHcO3334LhUIhdTmyl5qairfeegu7d++Gu7u71OU4Ha1Wi65duxqG5HTu3BlpaWlYs2YNQ6oVtmzZgv/+979Ys2YN2rRpg1OnTmHWrFkICwvDU089JXV5TomfI0Ty49QhlYv928bs2bOxZcsW7NixAy1atJC6HKfwyy+/ICcnB7169TK0aTQaHDlyBJ988gmuXr2KBg0aSFihvAUFBaF169ZGba1atUJGRoZEFTmXuXPnYurUqRg9ejQAoH379rh8+TIWL17MkFpDQUFBAIDr168jNDTU0M7PESLpOfWYVC72X3czZ87Epk2bsH37drRq1UrqcpzGsGHDcOTIERw8eNDwX9euXTF69GgcPHiQvavV6NmzJ86fP2/Udv78eTRv3lyiipzL7du3Ta54KBQKaLVaiSpyXkqlEkFBQUafIyUlJTh69Cg/R4gk5tQ9qQAX+6+LV199FV9//TX+85//wM/PzzA2y8vLC97e3hJXJ29+fn4mE8waNmwIf39/tGvXTpqinMhzzz2HBx54AO+++y5GjRqFkydPYtWqVZgzZ47UpTmFBx98EB988AGUSiXatGmDkydP4qOPPsJjjz0mdWmyVFhYiLS0NAAVQ00yMjJw8uRJ+Pv7o3nz5pgyZQree+89REVFITIyEu+++y68vLwwZswYiSsnqt+cfgkqoGIx/yVLluDatWto27Yt5s+fb7SWKokzN4t/5syZmD17tmOLuQsMGzaMS1DVwJ49e/DWW2/h/PnzCA0NRXx8PCZNmsRxgFYoKCjAv//9b+zcuRM3btxAUFAQRo8ejRkzZsDDw0Pq8mTn4MGDGD58uEn72LFjsXz5cuh0OixcuBCfffYZ8vLycO+99+Ldd9/lF04iid0VIZWIiIiI7i5OPSaViIiIiO5ODKlEREREJDsMqUREREQkOwypRERERCQ7DKlEREREJDsMqUREREQkOwyp5HQ6duyIKVOmSPLcBw8ehJ+fHw4ePGjT406ZMsVwe8b6YtiwYRg2bJjNj1tcXIy2bdti3bp1hrb169fDz88PKpXK0DZlyhR07NjR5s8vBbHX5VNPPcWbmhCRU2NIJcnpA0Tl/yIiIjB06FBs27ZN6vLqpKCgAO+++y769++P5s2bIygoCNHR0Xjttddw4cIFqcuzu6NHj2LBggXIy8tz2HOuWrUKgiBg7NixNX7sO++8g507d5q0nzlzBgsWLDAKuXL38ssvIzk5GSdPnpS6FCKiWmFIJdmYNWsWVq5ciRUrVmDatGkoKCjA008/jU2bNkldWq1cvHgR/fr1w/z58xEeHo6EhAS88847GDJkCHbu3ImePXtKXaLdHTt2DElJSbh165bJtq1bt2Lr1q02fT61Wo2PP/4YTzzxBNzd3Q3tjz32GLKyshAWFmZo+/DDD5GSkmL0+HfffRe7du0yOe5ff/2FpKQkXLp0yab12lPXrl3RuXNnLFu2TOpSiIhqxVXqAoj07r//fnTv3t3w8/jx49G6dWts2rTJ6e6hrVar8cQTTyArKwvbt2/HfffdZ7R9zpw5eOutt2zyXDqdDqWlpU53O8zKIdJWvv/+e1y7dg2jR482alcoFFAoFEZtbm5uNn/+mrp9+zYaNmxot+OPGjUKCxYsQH5+Pnx9fe32PERE9sCeVJItHx8fNGzYsNowUVZWhn//+98YMGAAlEolgoODcf/99+Obb74x2dfPzw8vv/wyvv/+e/Tt2xdBQUHo1q2baG9tamoqRo0ahZCQELRq1Qpz5sxBeXm5VbVv374dp0+fxvTp000CKgB4eHhg/vz5Ju3Xr1/HhAkT0Lx5cyiVSrz00ksoKSkR/TckJyejd+/eaNKkCTZv3gwAuHz5MuLj49GyZUsEBQXhvvvuw1dffWX0eJVKBT8/PyxevBjr1q1D165dERISguHDh+PixYsAgGXLlqFjx44IDg7G6NGjkZWVZXSMI0eOYPz48ejQoQOaNGmCNm3aYNq0aUaX9RcsWIA333wTANC5c2fDUA79uMmqY1Ir1/XVV1+he/fuaNKkCXr37o39+/dbdd537tyJkJAQtG7d2qjdmjGpfn5+KC0txVdffWWoddiwYVi/fj2eeeYZAMDw4cMN29avX2947IkTJ/Doo48iLCwMwcHBGDRoEL799lvRGn766SfMmjULrVq1QtOmTWt0DKBmr8v+/fujuLgYe/futer8ERHJCXtSSTby8/ORk5MDAMjOzsYnn3yCnJwcPPbYYxYfV1BQgE8//RQjR47EE088geLiYmzcuBHjxo3Dpk2bcP/99xvt/+uvv2LXrl2YMGECnnzySXz++eeYOHEiOnbsaAg32dnZGDZsGIqLi/H888+jUaNG+O9//4t9+/ZZ9W/ZvXs3AFRbe2VarRYjR45E+/bt8eabbyIlJQXr1q1DQEAA5s6da7Tv0aNHsW3bNsTHxyMoKAitWrVCTk4OHnzwQeTm5mLixIkIDg7Gli1bMGXKFOTl5ZlMNtu6dSuKi4vxz3/+E4WFhViyZAnGjRuH0aNHY/v27XjuueeQlZWFZcuWYfr06fjyyy+NHpubm4unnnoKQUFBOH36ND7//HP89ddf2LNnD4CKQJeamootW7Zg/vz5CAgIAACTAFnVtm3bkJOTgwkTJsDDwwPLly/HE088gVOnTsHf39/iY48dO4YuXbpYe8qNrFy5ElOnTkV0dDTGjx8PAGjSpAnCw8MRHx+P1atX45VXXkGrVq0AAD169AAAHDp0CKNHj0a7du3w2muvwd3dHVu3bsXYsWOxbt06jBgxwuh5Zs6ciXvuuQfTp09Hfn5+jY5R09dl+/bt4eHhgaNHjyI2NrZW54WISCoMqSQbVS/Rurm5YfHixdXOAPfz88Off/6JBg0aGNomTZqEvn37YunSpSYh9ezZszh8+LAhLMXGxqJDhw74z3/+g7fffhsA8MEHH+D69ev45ptv0Lt3bwAVww/EekXFnDt3Dr6+vmjevLlV+wNAeXk5hg4dioSEBADAP//5T+Tl5WHdunUmIfXcuXM4cOAAOnXqZGhLSEjAlStXsG3bNvTv399wjKFDhyIxMRGPP/447rnnHsP+GRkZ+O233+Dn5wcAcHFxwYIFC1BSUoIjR44YzmdhYSE++eQT3LhxA40bNwYAvPnmmyaXqaOjozFp0iQcO3YMPXv2RIcOHdCxY0ds2bIFw4YNg1KptOo8pKen4/jx44bnuu+++9CvXz9s2rQJ8fHxZh+nVquRlpaG//u//7Pqeap69NFH8eKLL6JFixZ49NFHjbb17NkTq1evxoABA9C3b19Du06nw8svv4x//OMf2LZtG1xcKi5OxcfHY8iQIZg7d65JSG3YsCF27twJV1fXGh+jpq9LV1dXNGvWDH///XetzgkRkZR4uZ9kIykpCcnJyUhOTsaqVaswcOBAvPLKK9XO8FcoFIZAVVZWhtzcXBQUFKBPnz74/fffTfbv27evUW9ekyZNEBUVZbjUDQB79uxB586dDUEAqAgX+h626hQUFMDHx8eqfSvTX1bW69OnD3JyclBQUGDU3qNHD6OAqq+5U6dOhoAKVIz7nDJlCoqKinDo0CGj/UeMGGEIqEBFyASAMWPGGAX+e++9FzqdzuhSuT6g6nQ6Qw+4vmdR7JzXRGxsrCGgAkCnTp3g6+tr9PsRk5ubC51OZ/RvsrdTp04hNTUVjzzyCHJzc5GTk4OcnBzk5uZi8ODBuHjxoslkq6efftoQUGt6jNq8Lv39/Q1XKIiInAl7Ukk2unXrZjRxasyYMejfvz9mzJiBoUOHWpxo8/nnn+Pjjz/GuXPnoNPpDO2CIJjsK9a76efnh9zcXMPPly9fxvDhw032i4yMtOrf4uPjU22oqsrNzQ0hISEmdQEVAaxy6G3RooXJ4y9duiRasz6QVw1LoaGhRj/rJ9Y0a9ZMtL3yeNOMjAzMnTsX33//vUmAFpvJXxNiv5977rnH6PdjSeXfv73plxF74YUX8MILL4juc+PGDaNVBar+7mpyjNq8LnU6nej7gIhI7hhSSbZcXFxw3333Yfny5bhw4QLatm0rut+mTZvw4osvYujQoXjppZcQGBgIV1dXrF+/Hhs3bjTZv+osb72q4Ubsg93aANS6dWucPHkSGRkZJmHQHP1lXmtq8/T0tOqYYo/VM3ceqjs/Wq0Wo0aNwo0bN/Dyyy+jVatW8PLyglarxejRo6HVaq2urTbPb06jRo0gCIJD12TV/1vfeOMNs2NhqwbIqr+7mh6jpq/LvLw8q4daEBHJCUMqyZparQYAFBUVmd1ny5YtaNGiBb788kujD/DKs69rqnnz5qLj+KxdgH/o0KHYuHEj/vvf/+LVV1+tdR01ERYWJlpzamqqYbstnD59Gn///Tc+/vhjPP7444Z2sXPjyB48hUKBiIiIOi24b65ec+3h4eEAAG9vbwwYMKBWz1mTY9T0dVleXo4rV67UepwuEZGUOCaVZKu8vBz79u2Du7u7YUa1GH3PW+XepIsXL4reOchaDzzwAP744w8cOXLE0Hb79m189tlnVj1+xIgR6NChA95//30cPXrUZHtpaSlef/31WtcnZsiQITh58iR++uknQ1t5eTlWrFiBhg0bWj3pqzpi5xsAli5darKvfuyqo3o3e/ToUacxsQ0bNhSt1dy/o0uXLoiIiMDSpUtFhzncuHGj2uesyTFq+rr8888/UVJSYhgvTETkTNiTSrLx448/Ii0tDUDFUjtbtmzB+fPn8fLLL1tciHzo0KHYsWMHxo4di6FDh+Lq1atYu3YtIiIicPr06VrVMm3aNGzYsAGPPfYYJk6caFjqx9qF111dXfGf//wHsbGxiImJwYgRI9C7d280aNAA58+fx5YtW3D9+nX8+9//rlV9Yl5++WVs2bIFY8eOxaRJkxAUFIStW7fi119/xfz5841m9tdFq1atEBERgYSEBFy9ehX+/v74/vvvcfXqVZN9u3btCgB4++23MXr0aLi7u6Nfv34IDAy0SS1VPfTQQ1i/fj3++usvs8NDLOnatSsOHDiApUuXomnTpmjcuDH69++Pzp07w8XFBYsXL8atW7fg6emJe++9Fy1atMCyZcswevRo9OzZE+PGjUNYWBiysrLw66+/4vLlyzh27JjF53RxcbH6GDV9Xe7fvx+enp4YNGhQjc8FEZHUGFJJNhYuXGj4fw8PD0RFReH999/HhAkTLD7u8ccfx40bN7B27Vrs378fLVu2xPz585GWllbrkNqkSRPs2rULM2fOxLJly+Dj44NHH30UgwYNwqhRo6w6RosWLfDTTz9h5cqV2L59O7777juo1Wo0b94cw4YNM1m3tK4CAgKwZ88evPnmm/j0009x+/ZtREZGYvny5bW6j705bm5u+O9//4tZs2Zh6dKlcHFxweDBg7F582aTHu/u3bsjISEBn332GZ5//nlotVrs2LHDbiF1yJAhhpsb6JfyqomFCxdi+vTpWLhwIYqKitCnTx/0798fISEh+OCDD/DBBx/gpZdegkajwUcffYQWLVqgV69e+PHHH7Fo0SJ89tlnyM/PR2BgIDp06IDZs2db9bzWHqOmr8vk5GTExMTY7AsKEZEjCXl5eY6bCktEZGcffPABVq5cid9//92wlNbnn3+OF198EX/++afJ6gV3qxMnTmDQoEHYv38/OnfuLHU5REQ1xjGpRHRXmTRpEgAY3Q722rVrEASh2jtW3U0WL16Mhx9+mAGViJwWe1KJ6K51/fp1bNu2DYsXL0bz5s0Nt2wlIiL5Y08qEd21zp07h7lz56JFixb4+OOPpS6HiIhqgD2pRERERCQ77EklIiIiItlhSCUiIiIi2WFIJSIiIiLZYUglIiIiItlhSCUiIiIi2fl/1UOINW7uqwYAAAAASUVORK5CYII=\n", "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "jwc_darkblue = jwc[jwc['Color'] == 'darkblue']\n", "jwc_gold = jwc[jwc['Color'] == 'gold']\n", "\n", "fig, ax = plt.subplots(figsize=(7,6))\n", "\n", "ax.scatter(jwc_darkblue['Bland Chromatin (jittered)'], \n", " jwc_darkblue['Single Epithelial Cell Size (jittered)'], \n", " label='Color=darkblue', \n", " color='darkblue')\n", "\n", "ax.scatter(jwc_gold['Bland Chromatin (jittered)'], \n", " jwc_gold['Single Epithelial Cell Size (jittered)'], \n", " label='Color=gold', \n", " color='gold')\n", "\n", "x_label = 'Bland Chromatin (jittered)'\n", "\n", "y_label = 'Single Epithelial Cell Size (jittered)'\n", "\n", "plt.ylabel(y_label)\n", "\n", "plt.xlabel(x_label)\n", "\n", "ax.legend(bbox_to_anchor=(1.04,1), loc=\"upper left\")\n", "\n", "plt.xlim(0, 11)\n", "\n", "plt.ylim(0, 11)\n", "\n", "plt.show()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "For instance, you can see there are lots of samples with chromatin = 2 and epithelial cell size = 2; all non-cancerous.\n", "\n", "Keep in mind that the jittering is just for visualization purposes, to make it easier to get a feeling for the data. We're ready to work with the data now, and we'll use the original (unjittered) data." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "First we'll create a training set and a test set. The data set has 683 patients, so we'll randomly permute the data set and put 342 of them in the training set and the remaining 341 in the test set." ] }, { "cell_type": "code", "execution_count": 13, "metadata": {}, "outputs": [], "source": [ "shuffled_patients = patients.sample(683, replace=False) \n", "training_set = shuffled_patients.take(np.arange(342))\n", "test_set = shuffled_patients.take(np.arange(342, 683))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Let's stick with 5 nearest neighbors, and see how well our classifier does." ] }, { "cell_type": "code", "execution_count": 14, "metadata": {}, "outputs": [ { "data": { "text/plain": [ "0.9706744868035191" ] }, "execution_count": 14, "metadata": {}, "output_type": "execute_result" } ], "source": [ "evaluate_accuracy(training_set, test_set, 5)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Over 96% accuracy. Not bad! Once again, pretty darn good for such a simple technique.\n", "\n", "As a footnote, you might have noticed that Brittany Wenger did even better. What techniques did she use? One key innovation is that she incorporated a confidence score into her results: her algorithm had a way to determine when it was not able to make a confident prediction, and for those patients, it didn't even try to predict their diagnosis. Her algorithm was 99% accurate on the patients where it made a prediction -- so that extension seemed to help quite a bit." ] }, { "cell_type": "code", "execution_count": null, "metadata": {}, "outputs": [], "source": [] } ], "metadata": { "anaconda-cloud": {}, "kernelspec": { "display_name": "Python 3", "language": "python", "name": "python3" }, "language_info": { "codemirror_mode": { "name": "ipython", "version": 3 }, "file_extension": ".py", "mimetype": "text/x-python", "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", "version": "3.6.12" } }, "nbformat": 4, "nbformat_minor": 1 }