{ "cells": [ { "cell_type": "code", "execution_count": 1, "metadata": { "tags": [ "remove_input" ] }, "outputs": [], "source": [ "path_data = '../../data/'\n", "\n", "import numpy as np\n", "import pandas as pd\n", "import math\n", "import scipy.stats as stats\n", "\n", "%matplotlib inline\n", "import matplotlib.pyplot as plt\n", "from mpl_toolkits.mplot3d import Axes3D\n", "plt.style.use('fivethirtyeight')\n", "\n", "import warnings\n", "warnings.filterwarnings('ignore')" ] }, { "cell_type": "code", "execution_count": 2, "metadata": { "tags": [ "remove_input" ] }, "outputs": [], "source": [ "def distance(point1, point2):\n", " \"\"\"Returns the distance between point1 and point2\n", " where each argument is an array \n", " consisting of the coordinates of the point\"\"\"\n", " return np.sqrt(np.sum((point1 - point2)**2))\n", "\n", "def all_distances(training, new_point):\n", " \"\"\"Returns an array of distances\n", " #between each point in the training set\n", " #and the new point (which is a row of attributes)\"\"\"\n", " attributes = training.drop(columns=['Class'])\n", " def distance_from_point(row):\n", " return distance(new_point, np.array(row)) # --- possible issue as original = np.array(new_point)\n", " return attributes.apply(distance_from_point, axis=1)\n", "\n", "def table_with_distances(training, new_point):\n", " \"\"\"Augments the training table \n", " with a column of distances from new_point\"\"\"\n", " training1 = training.copy()\n", " training1['Distance'] = all_distances(training1, new_point)\n", " return training1\n", "\n", "def closest(training, new_point, k):\n", " \"\"\"Returns a table of the k rows of the augmented table\n", " corresponding to the k smallest distances\"\"\"\n", " with_dists = table_with_distances(training, new_point)\n", " sorted_by_distance = with_dists.sort_values(by=['Distance'])\n", " topk = sorted_by_distance.take(np.arange(k))\n", " return topk\n", "\n", "def majority(topkclasses):\n", " ones = len(topkclasses[topkclasses['Class'] == 1])\n", " zeros = len(topkclasses[topkclasses['Class'] == 0])\n", " if ones > zeros:\n", " return 1\n", " else:\n", " return 0\n", "\n", "def classify(training, new_point, k):\n", " closestk = closest(training, new_point, k)\n", " topkclasses = closestk[['Class']]\n", " return majority(topkclasses)" ] }, { "cell_type": "code", "execution_count": 3, "metadata": { "tags": [ "remove_input" ] }, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
ClassAlcoholMalic AcidAshAlcalinity of AshMagnesiumTotal PhenolsFlavanoidsNonflavanoid phenolsProanthocyaninsColor IntensityHueOD280/OD315 of diulted winesProline
0114.231.712.4315.61272.803.060.282.295.641.043.921065
1113.201.782.1411.21002.652.760.261.284.381.053.401050
2113.162.362.6718.61012.803.240.302.815.681.033.171185
3114.371.952.5016.81133.853.490.242.187.800.863.451480
4113.242.592.8721.01182.802.690.391.824.321.042.93735
\n", "
" ], "text/plain": [ " Class Alcohol Malic Acid Ash Alcalinity of Ash Magnesium \\\n", "0 1 14.23 1.71 2.43 15.6 127 \n", "1 1 13.20 1.78 2.14 11.2 100 \n", "2 1 13.16 2.36 2.67 18.6 101 \n", "3 1 14.37 1.95 2.50 16.8 113 \n", "4 1 13.24 2.59 2.87 21.0 118 \n", "\n", " Total Phenols Flavanoids Nonflavanoid phenols Proanthocyanins \\\n", "0 2.80 3.06 0.28 2.29 \n", "1 2.65 2.76 0.26 1.28 \n", "2 2.80 3.24 0.30 2.81 \n", "3 3.85 3.49 0.24 2.18 \n", "4 2.80 2.69 0.39 1.82 \n", "\n", " Color Intensity Hue OD280/OD315 of diulted wines Proline \n", "0 5.64 1.04 3.92 1065 \n", "1 4.38 1.05 3.40 1050 \n", "2 5.68 1.03 3.17 1185 \n", "3 7.80 0.86 3.45 1480 \n", "4 4.32 1.04 2.93 735 " ] }, "execution_count": 3, "metadata": {}, "output_type": "execute_result" } ], "source": [ "wine = pd.read_csv(path_data + 'wine.csv')\n", "\n", "# For converting Class to binary\n", "\n", "def is_one(x):\n", " if x == 1:\n", " return 1\n", " else:\n", " return 0\n", "\n", "wine['Class1'] = wine['Class'].apply(is_one)\n", "\n", "# This creates a column 'Class1' - we drop the 'Class' column, rename 'Class1' as 'Class'\n", "# then move the column to the first position using 'pop' and 'insert'\n", "\n", "wine = wine.drop(columns=['Class'])\n", "wine = wine.rename(columns={'Class1': 'Class'})\n", "class_label = wine.pop('Class')\n", "wine.insert(0, 'Class', class_label)\n", "wine.head(5)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "# Accuracy of Classifier\n", "To see how well our classifier does, we might put 50% of the data into the training set and the other 50% into the test set. Basically, we are setting aside some data for later use, so we can use it to measure the accuracy of our classifier. We've been calling that the *test set*. Sometimes people will call the data that you set aside for testing a *hold-out set*, and they'll call this strategy for estimating accuracy the *hold-out method*.\n", "\n", "Note that this approach requires great discipline. Before you start applying machine learning methods, you have to take some of your data and set it aside for testing. You must avoid using the test set for developing your classifier: you shouldn't use it to help train your classifier or tweak its settings or for brainstorming ways to improve your classifier. Instead, you should use it only once, at the very end, after you've finalized your classifier, when you want an unbiased estimate of its accuracy." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Measuring the Accuracy of Our Wine Classifier\n", "OK, so let's apply the hold-out method to evaluate the effectiveness of the $k$-nearest neighbor classifier for identifying wines. The data set has 178 wines, so we'll randomly permute the data set and put 89 of them in the training set and the remaining 89 in the test set." ] }, { "cell_type": "code", "execution_count": 4, "metadata": {}, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
ClassAlcoholMalic AcidAshAlcalinity of AshMagnesiumTotal PhenolsFlavanoidsNonflavanoid phenolsProanthocyaninsColor IntensityHueOD280/OD315 of diulted winesProline
164013.782.762.3022.0901.350.680.411.039.580.701.68615
124011.874.312.3921.0822.863.030.212.912.800.753.64380
176013.172.592.3720.01201.650.680.531.469.300.601.62840
42113.881.892.5915.01013.253.560.171.705.430.883.561095
130012.861.352.3218.01221.511.250.210.944.100.761.29630
\n", "
" ], "text/plain": [ " Class Alcohol Malic Acid Ash Alcalinity of Ash Magnesium \\\n", "164 0 13.78 2.76 2.30 22.0 90 \n", "124 0 11.87 4.31 2.39 21.0 82 \n", "176 0 13.17 2.59 2.37 20.0 120 \n", "42 1 13.88 1.89 2.59 15.0 101 \n", "130 0 12.86 1.35 2.32 18.0 122 \n", "\n", " Total Phenols Flavanoids Nonflavanoid phenols Proanthocyanins \\\n", "164 1.35 0.68 0.41 1.03 \n", "124 2.86 3.03 0.21 2.91 \n", "176 1.65 0.68 0.53 1.46 \n", "42 3.25 3.56 0.17 1.70 \n", "130 1.51 1.25 0.21 0.94 \n", "\n", " Color Intensity Hue OD280/OD315 of diulted wines Proline \n", "164 9.58 0.70 1.68 615 \n", "124 2.80 0.75 3.64 380 \n", "176 9.30 0.60 1.62 840 \n", "42 5.43 0.88 3.56 1095 \n", "130 4.10 0.76 1.29 630 " ] }, "execution_count": 4, "metadata": {}, "output_type": "execute_result" } ], "source": [ "shuffled_wine = wine.sample(len(wine), replace=False) \n", "training_set = shuffled_wine.take(np.arange(89))\n", "training_set.head()" ] }, { "cell_type": "code", "execution_count": 5, "metadata": {}, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
ClassAlcoholMalic AcidAshAlcalinity of AshMagnesiumTotal PhenolsFlavanoidsNonflavanoid phenolsProanthocyaninsColor IntensityHueOD280/OD315 of diulted winesProline
122012.424.432.7326.51022.202.130.431.712.080.923.12365
112011.762.682.9220.01031.752.030.601.053.801.232.50607
40113.561.712.3116.21173.153.290.342.346.130.953.38795
74011.961.092.3021.01013.382.140.131.653.210.993.13886
144012.253.882.2018.51121.380.780.291.148.210.652.00855
\n", "
" ], "text/plain": [ " Class Alcohol Malic Acid Ash Alcalinity of Ash Magnesium \\\n", "122 0 12.42 4.43 2.73 26.5 102 \n", "112 0 11.76 2.68 2.92 20.0 103 \n", "40 1 13.56 1.71 2.31 16.2 117 \n", "74 0 11.96 1.09 2.30 21.0 101 \n", "144 0 12.25 3.88 2.20 18.5 112 \n", "\n", " Total Phenols Flavanoids Nonflavanoid phenols Proanthocyanins \\\n", "122 2.20 2.13 0.43 1.71 \n", "112 1.75 2.03 0.60 1.05 \n", "40 3.15 3.29 0.34 2.34 \n", "74 3.38 2.14 0.13 1.65 \n", "144 1.38 0.78 0.29 1.14 \n", "\n", " Color Intensity Hue OD280/OD315 of diulted wines Proline \n", "122 2.08 0.92 3.12 365 \n", "112 3.80 1.23 2.50 607 \n", "40 6.13 0.95 3.38 795 \n", "74 3.21 0.99 3.13 886 \n", "144 8.21 0.65 2.00 855 " ] }, "execution_count": 5, "metadata": {}, "output_type": "execute_result" } ], "source": [ "test_set = shuffled_wine.take(np.arange(89, 178))\n", "test_set.head()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "We'll train the classifier using the 89 wines in the training set, and evaluate how well it performs on the test set. To make our lives easier, we'll write a function to evaluate a classifier on every wine in the test set:" ] }, { "cell_type": "code", "execution_count": 6, "metadata": {}, "outputs": [], "source": [ "def count_zero(array):\n", " \"\"\"Counts the number of 0's in an array\"\"\"\n", " return len(array) - np.count_nonzero(array)\n", "\n", "def count_equal(array1, array2):\n", " \"\"\"Takes two numerical arrays of equal length\n", " and counts the indices where the two are equal\"\"\"\n", " return count_zero(array1 - array2)\n", "\n", "def evaluate_accuracy(training, test, k):\n", " test_attributes = test.drop(columns=['Class'])\n", " def classify_testrow(row):\n", " return classify(training, row, k)\n", " c = test_attributes.apply(classify_testrow, axis=1)\n", " return count_equal(c, test['Class']) / len(test)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Now for the grand reveal -- let's see how we did. We'll arbitrarily use $k=5$." ] }, { "cell_type": "code", "execution_count": 7, "metadata": {}, "outputs": [ { "data": { "text/plain": [ "0.898876404494382" ] }, "execution_count": 7, "metadata": {}, "output_type": "execute_result" } ], "source": [ "evaluate_accuracy(training_set, test_set, 5)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "The accuracy rate isn't bad at all for a simple classifier." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Breast Cancer Diagnosis\n", "Now I want to do an example based on diagnosing breast cancer. I was inspired by Brittany Wenger, who won the Google national science fair in 2012 a 17-year old high school student. Here's Brittany:\n", "\n", "![Brittany Wenger](http://i.huffpost.com/gen/701499/thumbs/o-GSF83-570.jpg?3)\n", "\n", "Brittany's [science fair project](https://sites.google.com/a/googlesciencefair.com/science-fair-2012-project-64a91af142a459cfb486ed5cb05f803b2eb41354-1333130785-87/home) was to build a classification algorithm to diagnose breast cancer. She won grand prize for building an algorithm whose accuracy was almost 99%. 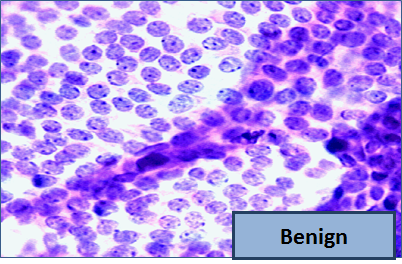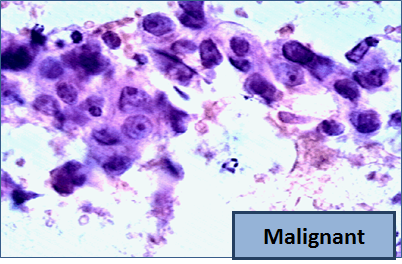\n", "\n", "Let's see how well we can do, with the ideas we've learned in this course.\n", "\n", "So, let me tell you a little bit about the data set. Basically, if a woman has a lump in her breast, the doctors may want to take a biopsy to see if it is cancerous. There are several different procedures for doing that. Brittany focused on fine needle aspiration (FNA), because it is less invasive than the alternatives. The doctor gets a sample of the mass, puts it under a microscope, takes a picture, and a trained lab tech analyzes the picture to determine whether it is cancer or not. We get a picture like one of the following:\n", "\n", "![benign](../../../images/benign.png)\n", "\n", "![cancer](../../../images/malignant.png)\n", "\n", "Unfortunately, distinguishing between benign vs malignant can be tricky. So, researchers have studied the use of machine learning to help with this task. The idea is that we'll ask the lab tech to analyze the image and compute various attributes: things like the typical size of a cell, how much variation there is among the cell sizes, and so on. Then, we'll try to use this information to predict (classify) whether the sample is malignant or not. We have a training set of past samples from women where the correct diagnosis is known, and we'll hope that our machine learning algorithm can use those to learn how to predict the diagnosis for future samples.\n", "\n", "We end up with the following data set. For the \"Class\" column, 1 means malignant (cancer); 0 means benign (not cancer)." ] }, { "cell_type": "code", "execution_count": 8, "metadata": {}, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
Clump ThicknessUniformity of Cell SizeUniformity of Cell ShapeMarginal AdhesionSingle Epithelial Cell SizeBare NucleiBland ChromatinNormal NucleoliMitosesClass
05111213110
154457103210
23111223110
36881343710
44113213110
.................................
6783111321110
6792111211110
6805101037381021
68148643410611
68248854510411
\n", "

683 rows × 10 columns

\n", "
" ], "text/plain": [ " Clump Thickness Uniformity of Cell Size Uniformity of Cell Shape \\\n", "0 5 1 1 \n", "1 5 4 4 \n", "2 3 1 1 \n", "3 6 8 8 \n", "4 4 1 1 \n", ".. ... ... ... \n", "678 3 1 1 \n", "679 2 1 1 \n", "680 5 10 10 \n", "681 4 8 6 \n", "682 4 8 8 \n", "\n", " Marginal Adhesion Single Epithelial Cell Size Bare Nuclei \\\n", "0 1 2 1 \n", "1 5 7 10 \n", "2 1 2 2 \n", "3 1 3 4 \n", "4 3 2 1 \n", ".. ... ... ... \n", "678 1 3 2 \n", "679 1 2 1 \n", "680 3 7 3 \n", "681 4 3 4 \n", "682 5 4 5 \n", "\n", " Bland Chromatin Normal Nucleoli Mitoses Class \n", "0 3 1 1 0 \n", "1 3 2 1 0 \n", "2 3 1 1 0 \n", "3 3 7 1 0 \n", "4 3 1 1 0 \n", ".. ... ... ... ... \n", "678 1 1 1 0 \n", "679 1 1 1 0 \n", "680 8 10 2 1 \n", "681 10 6 1 1 \n", "682 10 4 1 1 \n", "\n", "[683 rows x 10 columns]" ] }, "execution_count": 8, "metadata": {}, "output_type": "execute_result" } ], "source": [ "patients = pd.read_csv(path_data + 'breast-cancer.csv').drop(columns=['ID'])\n", "patients" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "So we have 9 different attributes. I don't know how to make a 9-dimensional scatterplot of all of them, so I'm going to pick two and plot them:" ] }, { "cell_type": "code", "execution_count": 9, "metadata": {}, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
ClassClump ThicknessUniformity of Cell SizeUniformity of Cell ShapeMarginal AdhesionSingle Epithelial Cell SizeBare NucleiBland ChromatinNormal NucleoliMitosesColor
00511121311gold
105445710321gold
20311122311gold
\n", "
" ], "text/plain": [ " Class Clump Thickness Uniformity of Cell Size Uniformity of Cell Shape \\\n", "0 0 5 1 1 \n", "1 0 5 4 4 \n", "2 0 3 1 1 \n", "\n", " Marginal Adhesion Single Epithelial Cell Size Bare Nuclei \\\n", "0 1 2 1 \n", "1 5 7 10 \n", "2 1 2 2 \n", "\n", " Bland Chromatin Normal Nucleoli Mitoses Color \n", "0 3 1 1 gold \n", "1 3 2 1 gold \n", "2 3 1 1 gold " ] }, "execution_count": 9, "metadata": {}, "output_type": "execute_result" } ], "source": [ "color_table = pd.DataFrame(\n", " {'Class':np.array([1, 0]),\n", " 'Color':np.array(['darkblue', 'gold'])}\n", ")\n", "patients_with_colors = pd.merge(patients, color_table, on='Class')\n", "\n", "patent_label = patients_with_colors.pop('Class')\n", "\n", "patients_with_colors.insert(0, 'Class', patent_label)\n", "\n", "patients_with_colors.head(3)" ] }, { "cell_type": "code", "execution_count": 10, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAqkAAAGTCAYAAAALL4uRAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAABaaElEQVR4nO3deVhUZf8G8PsAAirIACriAiLgvi+5i0uvSu6iuWaZAWL2e80Vk/TV3Nd8sUjRTMvcF1wyy1RC1BLT1EoDUUQBF2BAVFCc+f3By+gwMzjIwHlo7s91eeV8z5kzt88Z4+s55zlHUiqVahARERERCcRC7gBERERERAWxSSUiIiIi4bBJJSIiIiLhsEklIiIiIuGwSSUiIiIi4bBJJSIiIiLhsEklIiIiIuGwSSUAQGxsrNwRyjSOX/Fw/F4dx654OH5E4mKTSkRERETCYZNKRERERMJhk0pEREREwmGTSkRERETCsZI7ABEREcknNzcXDx8+lDsGmaGKFSvCyspwK8omlYiIyEzl5ubiwYMHUCgUkCRJ7jhkRtRqNZRKJezt7Q02qjzdT0REZKYePnzIBpVkIUkSFApFoUfx2aQSERGZMTaoJJeXfffYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIREZFZ2rJlC2rUqCF3DABAaGgomjRpUuztREVFQaFQIDU1Ve/yhIQEKBQKnD9/3uA2jFmnNLBJJSIiojLp7t27mDFjBpo3b46qVauiQYMGGDJkCH744Qe5o5EJ8D6pREREVOYkJCSgd+/esLOzw5w5c9C4cWOoVCpERkZi8uTJuHz5cqnkePLkCaytrUvls17myZMnckcwKR5JJSIiomJJSMiEv/8x9O17EP7+x5CQkFninzl16lSo1WocP34cgwYNgre3N+rVq4eAgACcPHkSAJCYmIhRo0ahZs2aqFmzJkaPHo3bt28Xut2NGzeiRYsWqFKlClq0aIFNmzZpLVcoFAgPD8fo0aNRvXp1zJs375Xyr169GnXr1kWNGjUQGBiIrKwsreW//fYbBg0ahDp16qBWrVro3bs3fv311yJnycnJwahRo9ClSxfcu3dPU4+Li0Pv3r3h4uKCNm3a4NixYwaz6ruEQN8lAVeuXMGbb76JmjVrwsvLC+PGjcOdO3eKPDb52KQSERHRK0tIyMTAgYexc+c1nDyZjJ07r2HgwMMl2qimp6fj6NGj8Pf3h52dnc5yhUIBtVqNUaNG4d69e9i/fz8OHDiAlJQUjBo1Cmq1Wu92Dxw4gGnTpiEoKAinT5/G+PHjMWXKFBw+fFhrvSVLlqBnz544deoU3nvvPQBAjRo1Cv01ZMgQzfv37t2L+fPnY+bMmYiMjIS3tzc+//xzrc948OABhg0bhsOHD+Onn35CkyZNMHToUJ1rTfVlyZeZmQk/Pz+kp6fj4MGDqFKlimbZnDlzEBgYiKioKHTt2hUjR45EUlKSEaOvX0pKCt544w00aNAAP/30E/bt24esrCyMGDECKpXqlbbJ0/1ERET0yubPj8H169oN6fXrmZg/Pwbh4d1L5DPj4+OhVqtRt25dg+ucOHECly9fxvnz5+Hu7g4AWL9+PVq0aIHIyEh07dpV5z1r1qzBsGHDEBAQAADw8vLChQsXsHr1avj6+mrWGzRoEMaMGaP13qioqEIz29raan4fFhaGESNGYOzYsQDyjgpHRUUhPj5es46Pj4/W+5cuXYr9+/fj6NGjGDZsmMEsiYmJAID79+8jICAArq6u+Oqrr7Q+HwDeffddDBo0CEBeo3vs2DF8+eWXCAkJKfTPYciGDRvQuHFjzJ07V1Nbu3YtateujfPnz6NVq1ZF3iabVCIiInplycmP9NZTUvTXTcHQkdAXXb16Fa6urpoGFQBq164NV1dXXLlyRW+TevXqVYwaNUqr1r59e50jqS1atNB5b506dYxMn/c5b731llatTZs2Wk3qvXv3sGDBAkRFReHevXt49uwZHj9+jFu3br00CwAMHjwYTZs2xddffw0rK912r02bNprfW1hYoFWrVrhy5YrRf4aCfv/9d5w6dUrv3RKuX7/OJpWIiIhKl6trBb31atX0103B09MTkiTh77//NriOWq02+NjNwh7HqW9ZwVrFihV11nnZrazat2+PXbt2FbrOi4KCgnD37l0sXLgQbm5usLGxQf/+/XUmR+nLAgC9evXC3r178ccff6BZs2ZGf64+FhZ5V4e++I+D3NxcrXVUKhV69uyJ+fPn67z/xcsMioJNKhEREb2ykJDWiIm5p3XK38OjEkJCWpfYZzo6OqJHjx4IDw9HYGCgznWpSqUS9evXR1JSEhISEjRHU2/cuIHk5GTUr19f73br1auHM2fOaB3lPH36tMH1X1SU0/316tVDTEyM1ufExMRorX/mzBksXrwYvXr1ApB3u62iTEKaNWsWHB0dMXDgQERERKBp06Zay2NiYjSXFKjVavz2228YMGCA3m1VrlwZQN51p/m/v3TpktY6zZo1w969e1GrVi2UK1fO6JyFYZNKREREr8zdvRL27fPF/PkxSEl5hGrVKiAkpDXc3SuV6OcuX74cvXr1Qrdu3TBr1iw0atQIarUaUVFRWLVqFS5duoTGjRsjICAAS5YsgVqtxvTp09GsWTN06dJF7zY/+OADvPPOO2jevDm6d++Oo0ePYufOnfj6669fmqcop/vHjx+P8ePHo2XLlujUqRMiIiJw7tw5KBQKzTqenp7YsWMHWrdujUePHmH27NlFvtXVxx9/DLVarWlUX3xYwJdffgkvLy80bNgQ69evR2JiIt59912Df7aaNWti8eLF+M9//oObN29i2bJlWuu899572LRpE8aOHYtJkyahcuXKuHHjhmaSmL29fZGyA2xSiYiIqJjc3SuV2CQpQ2rXro3IyEisWLECc+bMQXJyMpycnNC4cWOsWrUKkiRhy5YtmDFjBvr27QsgbzLS0qVLDZ7u79u3L5YuXYrQ0FDMnDkTtWrVwooVK7QmTZnC4MGDcePGDXzyySd4/PgxfH19MWHCBHz77beaddasWYNJkyaha9euqFatGoKDgw0+Raows2fPhlqtxoABAxAREYFKlfL+8TBnzhx89tln+P3331GrVi188803Bi9ZKFeuHDZs2IApU6agU6dOaNKkCWbPnq01gcvV1RVHjhzB3Llz4efnh5ycHNSsWRPdunWDjY1NkXMDgKRUKl9+9TH948XGxsLb21vuGGUWx694OH6vjmNXPOY+fhkZGXBwcJA7Bpmxwr6DvE8qEREREQmHTSoRERERCYdNKhEREREJR9YmNTo6GsOHD0eDBg2gUCiwZcsWreVqtRqLFi1C/fr1Ua1aNfTp0wd//fWXTGlfjZSbgPLp/qh4vy/Kp/tDyk2QO5KW/Octjx9/vtSet1wUCxachaNjOBSKcDg6hmPBgrNyR9Kye3ccqlffiLZtT6B69Y3YvTtO7kha8vM5O4cLmU9kon/38vO1aXNCyHyif/dEHz8ikrlJffjwIRo2bIjFixejfPnyOstXr16Nzz77TPO4ripVqmDQoEF48OCBDGmLTspNQMW0gbDO3gmrpydhnb0TFdMGCtOovvi85XPnMkrlectFsWDBWSxbdgH59w5Wq4Flyy4I88Nk9+44jBt3HI8e5UKlAh49ysW4cceF+WH8Yr5nz8TLJzLRv3ui5xP9uyf6+BFRHmFm99eoUQNLly7VPI5MrVajfv368Pf3x9SpUwEAjx8/hre3Nz755BPN825FVj7dH9bZO3XqT2yH4rFjuAyJtPn7H8POndd06kOHepb6rUT0cXQMh74n30kSkJ7uX/qBCqhefSMePcrVqVeoYIWkJPm/n6Lne5FoM6xF/+6Jnk/0757o41eaOLuf5FbYd1DY+6QmJCTgzp076N79ebNUvnx5dOjQAb/88ovBJjU2Nra0Ir5UXdt4WOsZ4eyseMTelz9nfPx9A/VUIcbR0KOZ1Wox9nN2tu4P4fw68xWdSJlE/+6Jnk/0757o45dPpH+4EclB2CY1/9FfBZ/3WqVKFSQnJxt8n0h/qW3T6wDZ53TrdnXgXUv+nHXqJOLcuQw9dWchxlGSThg82iFCPlvbk3qPFtnaWjFfEYl2JFX0757o+UT/7ok+fkSUR/jZ/QWfCqFWqw0+KUI02fYheGbpoVV7ZumBbPsQmRJpCwlpDQ8P7cfWlfTzloti6tTmRaqXttDQzkWqlzbR84lM9O+e6PlE/+6JPn5ElEfYJtXFxQUAcPfuXa36/fv3dY6uikpt5Y6HTvvwxHYocst1xhPboXjotA9qK3e5owF4/rzloUM90aqVAkOHemLfPt8Sf96ysWbNaoNp05oj/98kkgRMm9Ycs2a1kTfY//j5eWHDhm6oUMEKFhZ519tt2NANfn5eckcDoJ3P0lK8fCIT/bsnej7Rv3uijx+Vni1bthh8FGhZoFAoEBERYXB5amoqFAoFoqKiSjGV6Qg/cSogIABTpkwBAGRnZ8Pb2xvz5s0rExOnyhLRTreWNRy/4uH4vTqOXfGY+/iV9YlTd+/exYoVK3DkyBEkJSXB2dkZjRo1QkBAAHr27PnS92/ZsgXTp0/H7du3SyGt6SkUCmzatAkDBgzQuzw1NRWenp44cOAAOncW40xGQcJOnMrKykJ8fDwAQKVS4datW7h48SIcHR1Rq1YtBAUFYcWKFfD29oaXlxeWL1+OihUrYsiQIXLGJiIiIpklJCSgd+/esLOzw5w5c9C4cWOoVCpERkZi8uTJuHz5cqnkePLkCaytrUvls8yNrKf7z58/jy5duqBLly54/PgxFi1ahC5dumDhwoUAgH//+9+YMGECpk2bhm7duiElJQV79uyBvb29nLGJiIjoBXI8uGbq1KlQq9U4fvw4Bg0aBG9vb9SrVw8BAQE4efIkACAxMRGjRo1CzZo1UbNmTYwePfqlR003btyIFi1aoEqVKmjRogU2bdqktVyhUCA8PByjR49G9erVMW/evFfKv3LlSnh7e6NGjRoIDAzE4sWL0aRJE81ylUqFpUuXolGjRqhatSo6dOiAQ4cOFbrN3377DT4+PnBxcUHnzp0RExPzStlEIeuR1M6dO0OpVBpcLkkSZs6ciZkzZ5ZeKCIiIjJa/oNrLJ9dzys8BSyfxpToHIz09HQcPXoUISEhsLOz01muUCigVqsxatQo2NraYv/+/ZAkCdOmTcOoUaNw/PhxvZOwDxw4gGnTpmHhwoXo3r07fvrpJ0yZMgVVq1aFr6+vZr0lS5Zg9uzZmD9/vqb2smtb27dvj127dgEAdu/ejSVLlmDZsmXo0KED9u/fj08//VTrtHdYWBhCQ0OxcuVKtGjRAtu3b8dbb72FEydOoGnTpjrbf/jwId5880107NgRYWFhSE5OLvP9k7C3oCIiIiLx2T6Y/7xB/R/LZ9dh+2B+iT24Jj4+Hmq1GnXr1jW4zokTJ3D58mWcP38e7u55zfL69evRokULREZGomvXrjrvWbNmDYYNG4aAgAAAgJeXFy5cuIDVq1drNamDBg3CmDFjtN77sslJtra2mt9/8cUXGDlypGYbkydPRlRUFOLinj+Vbc2aNZg4cSKGDh0KAJg1axZOnTqFNWvWYN26dTrb37lzJ548eYLPPvsMdnZ2aNiwIaZMmYLAwMBCc4mMTSoRERG9Motn+u9dbvEspcQ+U23oiQwvuHr1KlxdXTUNKgDUrl0brq6uuHLlit4m9erVq5oJ3Pnat2+Pw4cPa9VatGih8946deoYmR74+++/dZrcVq1aaZrUzMxMJCcno127djpZfvjhB73bvHr1Kho1aqR1ZPm1114zOpOI2KQSERHRK1NZugJP9dWrldhnenp6QpIk/P333wbXKey+6oXdb13fsoK1ihUr6qxTlNP9L8tQGEPvM6ZxL2vYpBIREdEry7YPgeXTGK1T/iX94BpHR0f06NED4eHhCAwM1LkuValUon79+khKSkJCQoLmaOqNGzeQnJyM+vXr691uvXr1cObMGbz11lua2unTpw2u/6KinO6vW7cufvvtN4wePVpT++233zS/r1SpElxdXXHmzBn4+PhoZalXr57e7devXx9bt27Fw4cPNU302bNnX5pbZGxSiYiI6JXlP7jG9sF8WDxLgcqyGrLtQ0r8wTXLly9Hr1690K1bN8yaNQuNGjWCWq1GVFQUVq1ahUuXLqFx48YICAjAkiVLoFarMX36dDRr1gxdunTRu80PPvgA77zzDpo3b47u3bvj6NGj2LlzJ77++uuX5inK6f7x48fj/fffR4sWLdChQwccPHgQMTExUCgUWlkWLVoET09PNG/eHNu3b8fp06dx4sQJvdscMmQIPvnkE0ycOBHTp09HSkoKVqxYYXQmEbFJJSIiomJRW7mX2CQpQ2rXro3IyEisWLECc+bMQXJyMpycnNC4cWOsWrUKkiRhy5YtmDFjBvr27QsA8PHxwdKlSw2eMu/bty+WLl2K0NBQzJw5E7Vq1cKKFSu0Jk2Zgp+fH27cuIG5c+fi8ePH6Nu3L95991189913mnXGjx+PrKwszJkzB3fv3oW3tzc2b96sd2Y/ANjZ2WH79u2YPHkyfHx84O3tjf/85z8YMWKESbOXJmGeOEXyMvenrhQXx694OH6vjmNXPOY+fmX9iVP/JKNGjUJubi62b98ud5RSJewTp4iIiIjMzaNHj7Bhwwa8/vrrsLKywv79+/Hdd99h8+bNckcTCptUIiIiolIkSRKOHj2KlStXIjs7G3Xq1MHatWvRr18/uaMJhU0qERERUSkqX748IiIi5I4hPAu5AxARERERFcQmlYiIiIiEwyaViIjIjP0Tn1REZcPLvntsUomIiMxUxYoVoVQq2ahSqVOr1VAqlXofMZuPE6eIiIjMlJWVFezt7ZGZmSl3FDJD9vb2sLIy3IqySSUiIjJjVlZWvKE/CYmn+4mIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4nN1PRKRHQkIm5s+PQXLyI7i6VkBISGu4u1eSO5ZGfr74+PuoUydRuHxERMXFJpWIqICEhEwMHHgY168/v3dkTMw97NvnK0QjWDDfuXMZQuUjIjIFnu4nIipg/vwYrQYVAK5fzztyKQLR8xERmQKbVCKiApKTH+mtp6Tor5c20fMREZkCm1QiogJcXSvorVerpr9e2kTPR0RkCmxSiYgKCAlpDQ8P7Ws7PTwqISSktUyJtImej4jIFDhxioioAHf3Sti3zxfz58cgJeURqlUTa3b/i/ni41NRp46zUPmIiEyBTSoRkR7u7pUQHt5d7hgG5eeLjY2Ft7e33HGIiEyOp/uJiIiISDhsUomIiIhIOK/UpN66dQsXLlxAVlaWqfMQERERERWtST148CBatmyJpk2bonv37jh37hwAIDU1FR06dMCBAwdKJCQRERERmRejm9QjR45gzJgxqFy5MmbMmAG1Wq1Z5uzsjJo1a+Lbb78tkZBEREREZF6MblKXLl2Ktm3b4ocffoC/v7/O8jZt2uDSpUsmDUdERERE5snoJvXPP//E4MGDDS53cXHB/fv3TRKKiIiIiMyb0U2qtbU1cnJyDC5PTExEpUq8kTQRERERFZ/RTWq7du2wd+9evcsyMzOxZcsWdO7c2WTBiIiIiMh8Gd2kBgcH448//sDAgQNx+PBhAMDFixfx5ZdfwsfHB5mZmZg+fXqJBSUiIiIi82F0k9qiRQvs2rULt2/fxsSJEwEAs2fPxpQpU2BpaYldu3ahXr16JRaUiIiIiMyHVVFW7tSpE86ePYtLly7h2rVrUKlU8PDwQPPmzSFJUkllJCIiIiIzU6QmNV+TJk3QpEkTU2chIiIiIgJQhNP9jo6OqFu3LqKjo/Uu37FjB5ycnEwWjIiIiIjMV5Eei5qTk4OBAwciLCyspPIQERERERWtSV24cCFGjhyJjz76CAEBAcjOzi6pXERERERkxorUpFpbW2P16tVYuXIlIiIi0KtXLyQmJpZUNiIiIiIyU0VqUvONHTsW+/fvR0pKCrp27YrIyEhT5yIiIiIiM/ZKTSoAtG3bFidOnICHhwf8/Pzw9ddfmzIXEREREZmxV25SAcDV1RXfffcdRowYgZMnT5oqExERERGZOaPvk/r777+jcuXKOnVra2uEhoaif//+uHfvnknDEREREZF5MrpJdXNzK3T5v/71r2KHISIiIiICCmlS82/a37FjR63XL5O/PhERERHRqzLYpPbt2xeSJCElJQXW1taa14ao1WpIkoS0tDSThXv27BkWLVqEHTt24M6dO3BxccGbb76J4OBgWFm90hNdiYiIiKgMMNjpHThwAEDeNacvvi5Nn376KdavX4+wsDA0bNgQf/zxB4KCgmBtbY3p06eXeh4qfed++RUZsbPg7JCO1AxHOHgvQKu2r8kdS2P37jh88EEUsrNzYWt7EqGhneHn5yV3LI3vD0ZCfWcuXJwzcCfVAZLLHPTu6yN3rDJh2rSTCA//S/Pa378Bli3rJGMibaJ/90QXHZ2EoKBIpKU9hpNTDMLCfNCxY3W5YxHRCySlUqmWO4Qhw4YNg6OjI7744gtNbfz48UhPT8f27dtlTPbPExsbC29vb7ljaDn3y69wwwh4uaVqanE3nXETW4VoVHfvjsO4ccd16hs2dBOiWfj+YCRaVR4LL/fnZzfiEpxw7v5G4RpV0b5/BRvUfKI0qqJ/90QXHZ2EAQO+Q27u8x9/VlYSIiLeYKNKJJBi3YLq9u3bOHfuHJRKpYniaGvXrh1OnjyJv//+GwBw5coVREVFcZKWmciInaXVoAKAl1sqMmJnyZRI2wcfRBWpXtrUd+ZqNagA4OWeBvWduTIlKjv0NaiF1Uub6N890QUFRWo1qACQm6tGUBAfTEMkkkIv7IyJicFPP/2Ed999F1WqVNHU79y5g3HjxuHUqVMAAEtLS0yYMAFz55r2h9+kSZOQlZWFtm3bwtLSErm5uZg6dSree+89g++JjY01aQZzItrYOTmk669XShcia3Z2rsG6CPlcnDP01qs6ZwiRryARM+kjQk7Rv3uiS0t7bLAu0viJdHaBSA6FNqkbNmxAVFQUZsyYoVV///33ER0djQ4dOqBly5Y4ceIEQkNDUb9+fYwYMcJk4fbs2YNt27Zh/fr1qF+/Pi5duoTg4GC4ublhzJgxet/Dv9SvRrTTrQBw7BdHvfW0TEc0FyCrre1JPHqk2yzY2loJMZaHf3bQW7+b6oBWAuR7kXjfvxMGl4iQU/TvnuicnGKQlZWlp16e40ckkEJP98fExKBPnz5atevXr+Onn35C9+7dcejQIXzyySc4duwYGjZsaPJHo86ePRsTJ06En58fGjVqhOHDh+P999/HqlWrTPo5JCYH7wWIu+msVYu76QwH7wUyJdIWGtq5SPXSJrnMQVyCk1YtLsEJksscmRKVHf7+DYpUL22if/dEFxbmAysr7bvVWFlJCAsT61ptInNXaJN6584dnX9VHjlyBJIk4Z133tHUypUrhyFDhuDPP/80abhHjx7B0tJSq2ZpaQmVSmXSzyExtWr7Gm5iK/b+1AY/x3hh709thJk0BQB+fl7YsKEbKlSwgoUFUKGClVATV3r39cG5+xux7buWOP6LJ7Z911LISVMiWrask05DKsqkKUD8757oOnasjoiIN+DmZgc7O0u4udlx0hSRgF56s1G1Wvvi8l9//RWA7k37q1SpgseP9V/n86p69+6NTz/9FO7u7qhfvz4uXryIzz77DMOHDzfp55C4WrV9DWj7o9wxDPLz84Kfn5eAp6vz5DWkx+SOUSYtW9ZJmKZUH9G/e6Lr2LE6Ll4cwfEjElihR1I9PDxw5swZzevc3FxERUWhbt26cHLSPo2YmpqKypUrmzTc0qVL0b9/f0yZMgVt27ZFSEgI3n77bXz88ccm/RwiIiIiEkuhR1JHjBiBkJAQeHt7o0OHDti1axdSU1Mxfvx4nXWjo6Ph5WXaU0329vZYvHgxFi9ebNLtEhEREZHYCm1Sx40bh+PHj2PJkiWQJAlqtRqdO3fG+++/r7VeYmIijh07htmzZ5doWCIiIiIyD4U2qeXKlcP27dtx/vx5XL9+HW5ubmjdurXOek+fPsX69et1rlMlIiIiInoVL504BQAtWrRAixYtDC6vU6cO6tSpY7JQRERERGTeivVYVCIiIiKiksAmlYiIiIiEwyaViIiIiITDJpWIiIiIhMMmlYiIiIiEwyaViIiIiIRj8BZUS5YsKfLGJEnC9OnTixWIiIiIiMhgk/oqjyJlk0pEREREpmCwSU1PTy/NHEREREREGrwmlYiIiIiEwyaViIiIiIRj8HR/v379irwxSZKwf//+YgUiIiIiIjLYpKpUKkiSVKSNqdXqYgciIiIiIjLYpB46dKg0cxARERERafCaVCIiIiISTpGa1GfPnmHHjh2YOHEihg0bhsuXLwMAlEol9u7di5SUlBIJSURERETmxegmNSMjAz179kRgYCAiIiLw448/IjU1FQBgb2+PWbNmYd26dSUWlIiIiIjMh9FN6ty5c3HlyhXs3LkTFy5c0JokZWlpiX79+uHHH38skZBEREREZF6MblIPHTqEgIAAvP7663pn/Xt6eiIxMdGk4YiIiIjIPBmc3V+QUqmEh4eHweVqtRpPnjwxSSiifEkJl3H/r5moYHMfj3Iqo3KDRaju3ljuWBrnfvkVGbGz4OSQjmO/OMLBewFatX1N7lgaCQmZmD8/BsnJj+DqWgEhIa3h7l5J7lhlQnR0EoKCIqFU5kChsEFYmA86dqwudyyN/H0bH38fdeokCrdvRf/uiT5+RFSEJtXNzQ1//vmnweXR0dHw8vIySSgiIK9BLX9/EDo3u6ep3UgahCTsFaJRPffLr3DDCHj1SNXU4m6OwLlftgrRqCYkZGLgwMO4fj1TU4uJuYd9+3z5w/gloqOTMGDAd8jNzbusKTPzKQYM+A4REW8I0agW3LfnzmUItW9F/+6JPn5ElMfo0/1Dhw7F5s2bER0dranln/Zfu3YtDh48iJEjR5o+IZmt+3/NRO3q97Rqtavfw/2/ZsqUSFtG7Cx4uaVq1bzcUpERO0umRNrmz4/RahIA4Pr1vKNHVLigoEhNg5ovN1eNoKBImRJpE33fMh8RmYLRR1I//PBDxMTEoH///vDy8oIkSQgODkZaWhru3LmDPn36IDAwsCSzkpmpYHPfQD1Vb720OTukF6le2pKTH+mtp6Tor9NzSmWO3npGhv56aRN93zIfEZmC0U1quXLlsGPHDuzcuRP79u2DJEnIzc1Fs2bNMHjwYLz55ptFfowqUWEe5VQ2UHcu5ST6pWY4Fqle2lxdK+itV6umv07PKRQ2yMx8qlN3cLCRIY0u0fct8xGRKUhKpVL98tXony42Nhbe3t5yx9CSf03qi6f8byRVwePKgl2T6vbiNanOuAlxr0n18Kgk5HV3on3/Cl6TCgBWVpKw16QCYu1b5iMiU3hpk7p7927Y2dmhV69eBtc5cuQIHj58iMGDB5s8IJUO0ZqEfM9n96fiUY6zuLP7K6UjLVPc2f0pKY9QrZp4M6zzifj9y5/dn5GRAwcHkWf3p6JOHWfh9q3o3z3Rx4+IXtKkHjx4EGPGjMGOHTvw+uuvG9zITz/9hKFDh2Lbtm3o2bNniQSlkiVik1CWcPyKh+P36jh2xcPxIxJXobP7t2zZgvbt2xfaoAJAjx490LFjR2zatMmk4YiIiIjIPBXapJ47d67Q0/wv+te//oWYGN6+g4iIiIiKr9AmValUwtnZuJnUzs7OSE8X49Y7RERERFS2FdqkOjg4IDk52agNpaSkwMHBwSShiIiIiMi8FdqktmzZEhEREUZtaN++fWjZsqVJQhERERGReSu0SX3nnXdw+fJlBAcHQ6VS6V1HrVZj5syZ+OOPPzB27NgSCUlERERE5qXQJ075+vpi1KhRWLt2LU6cOIEhQ4agYcOGsLOzQ1ZWFv7880/s2rULV69exVtvvYXevXuXVm4iIiIi+gd76WNR16xZg7p16+LTTz/FggULtB59qlaroVAoMG/ePHzwwQclGpSIiIiIzMdLm1QA+L//+z8EBATgzJkzuHr1Kh48eAB7e3vUq1cP7dq1g62tbUnnJCIiIiIzYlSTCgC2trbo2rUrunbtWoJxiIiIiIheMnGKiIiIiEgObFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOAZvQbVkyZIib0ySJEyfPr1YgYiIiIiIDDapixcvLvLG2KQSERERkSkYbFLT09NLMwcRERERkQavSSUiIiIi4bBJJSIiIiLhGDzdr8+VK1fwxRdf4MKFC8jIyIBKpdJaLkkSLly4YMp8RERERGSGjD6S+ssvv6Bbt244dOgQXFxccOPGDdSuXRuurq5ITExExYoV0aFDh5LMSkRERERmwugmdf78+ahevTrOnj2Lzz//HAAwefJkfP/99zh8+DBu376NIUOGmDxgSkoKxo8fD09PT7i4uKBt27Y4efKkyT/HXEVHJ6Fp063o1i0KTZtuRXR0ktyRtHzxxSU4O6+HQhEOZ+f1+OKLS3JH0jJt2kkoFOFo0+YEFIpwTJsm1ndT9PFLSMiEv/8xjB9/Hv7+x5CQkCl3JI2xo9fiwLpuOLevFQ6s64axo9fKHUmL6N+9/H3bt+9B4fYtACxYcBaOjnnj5+gYjgULzsodiYgKMPp0//nz5zFt2jQoFArNzP/80/1t27bF22+/jQULFqB79+4mC6dUKtGrVy+0a9cOO3bsgLOzMxISElClShWTfYY5i45OwoAB3yE3Vw0AyMrKwoAB3yEi4g107Fhd5nR5DVZw8BnN62fP1JrX48c3kSuWxrRpJxEe/pdWLf/1smWd5IikRfTxS0jIxMCBh3H9el7zcu5cBmJi7mHfPl+4u1eSNdvY0WuxdOISeLmnaWrtmiZg7Ghg4zeBMibLI/p3r+C+BSDMvgXyGtRlyy5oXqvV0LyeNauNPKGISIfRR1IlSYKDgwMAoEKFCgCAtLTn/wP38vLCX3/9pfe9r+q///0vqlWrhrVr16JVq1aoXbs2fHx8UK9ePZN+jrkKCorUNKj5cnPVCAqKlCmRtlmzfilSvbQVbBJeVi9too/f/PkxWk0MAFy/non582NkSvTc4C7btBpUAPByT8PgLttkSqRN9O+eyPsWAJYvv1CkOhHJw+gjqW5uboiPjwcA2NjYwN3dHcePH4efnx8A4NSpU3BycjJpuEOHDqFHjx4YO3YsoqKiUK1aNYwZMwb+/v6QJEnve2JjY02a4Z8sLe2xwboI4/jsmdpgXYR8hREhn+jjFx9/30A9VfZ81avqPzVdvUqm7NleRoR8Iu9bIO/IqaG6CPnyeXt7yx2BSFZGN6ndunVDREQE5s6dC0mS8Pbbb2PevHm4efMm1Go1Tp48iUmTJpk03I0bN7BhwwZMmDABkyZNwqVLlzBjxgwAQEBAgN738C+18ZycYpCVlaWnXl6IcbS0jNTbaFlaSkLkA04YXCJCPtHHr06dRJw7l6Gn7ix7vgPH9Z+STrpXCa0EGDvRv3si71sAkKQTehtVSRJj/Igoj9Gn+6dOnYpNmzYhNzcXADBp0iR8/PHHSE9Px4MHDxAcHIyPPvrIpOFUKhWaNWuGOXPmoFmzZhg9ejQCAwOxfv16k36OuQoL84GVlfYRaSsrCWFhPjIl0rZgQdsi1Uubv3+DItVLm+jjFxLSGh4e2s2gh0clhIS0linRc3t+Ho64BO0zQ3EJTtjz83CZEmkT/bsn8r4FgKlTmxepTkTykJRKpYETH/Jr3LgxunXrhtDQUE1t27ZtmDx5MpKSxJqFXlZFRychKCgSaWmP4eRUHmFhPkJMmsr3xReXMGvWL3j2TA1LSwkLFrQVYtJPvoITWPz9GwgxcSWf6OOXkJB3nWJ8fCrq1HFGSEhrISbWAHmTpwZ32YbqVTKRdK8S9vw8XIhJU/lE/+7l79uUlEeoVq2CUPsWyJs8tXz5BajVeUdQp05tzklTRIIRukl97733cPv2bRw+fFhTmz9/Pg4cOIBffhFj8sc/RWxsLE9zFQPHr3g4fq+OY1c8HD8icRm8JnXJkiWQJAlTp06FhYUFlixZ8tKNSZKE6dOnmyzchAkT0LNnTyxfvhyDBw/GxYsXsW7dOnz88ccm+wwiIiIiEo/BI6mOjo6QJAkpKSmwtraGo6PjyzcmSVq3pTKFI0eOYN68eYiLi0PNmjXh7++PwMBAg7P76dXwaELxcPyKh+P36jh2xcPxIxKXwSOp+TfsN/S6tPTq1Qu9evWS5bOJiIiISB5Gz+4nIiIiIiotbFKJiIiISDgGT/f369evyBuTJAn79+8vViAiIiIiIoNNqkqlKvLkJLWhZ80RERERERWBwSb10KFDpZmDiIiIiEiD16QSERERkXCK1KQ+e/YMO3bswMSJEzFs2DBcvnwZAKBUKrF3716kpKSUSEgiIiIiMi9GN6kZGRno2bMnAgMDERERgR9//BGpqakAAHt7e8yaNQvr1q0rsaBEREREZD6MblLnzp2LK1euYOfOnbhw4YLWJClLS0v069cPP/74Y4mEJCIiIiLzYnSTeujQIQQEBOD111/XO+vf09MTiYmJJg1HRERERObJ6CZVqVTCw8PD4HK1Wo0nT56YJBQRERERmTejm1Q3Nzf8+eefBpdHR0fDy8vLJKGIiIiIyLwZ3aQOHToUmzdvRnR0tKaWf9p/7dq1OHjwIEaOHGn6hERERERkdgzezL+gDz/8EDExMejfvz+8vLwgSRKCg4ORlpaGO3fuoE+fPggMDCzJrERERERkJoxuUsuVK4cdO3Zg586d2LdvHyRJQm5uLpo1a4bBgwfjzTffLPJjVImIiIiI9DG6Sc03dOhQDB06tCSyEBEREREB4GNRiYiIiEhARTqSeuLECWzatAk3btxAenq61g39gbyJVBcuXDBlPiIiIiIyQ0Y3qWFhYZg1axYqV66M1q1bo0GDBiWZi4iIiIjMmNFN6meffYaOHTti9+7dsLa2LslMRERERGTmjL4mNTU1FYMHD2aDSkREREQlzugmtXnz5rh582ZJZvlHupvwA7L/8IYUVx3Zf3jjbsIPckcqU37+YTvSYzygulIN6TEe+PmH7XJH0vL9wUgc3tAdD/4YjsMbuuP7g5FyR9KyYMFZODqGQ6EIh6NjOBYsOCt3JC0JCZnw9z+G8ePPw9//GBISMuWOpNG+/TYoFOGaX+3bb5M7kpb8fdumzQkh9210dBKaNt0KN7ev0LTpVkRHJ8kdSUt+vm7dooTMR0SApFQq1S9fDfjtt98wYsQIhIeHo0uXLiWd6x/hbsIPqC0NR7lyKk3t6VML3FBvQ1X3njIm0xUbGwtvb2+5Y2j5+Yft6FU/CNYvjN+TpxY4ciUMXXoOkzFZnu8PRqJV5bHwck/T1OISnHDu/kb07usjY7I8CxacxbJlF3Tq06Y1x6xZbUo/UAEJCZkYOPAwrl9/3ph6eFTCvn2+cHevJGOyvAb1r78e6NQbNLDH6dPDZUikTfR9Gx2dhAEDvkNu7vMfL1ZWEiIi3kDHjtVlTJZH9HxElMdgk6rvXqg3btzAtWvX4OnpiVq1asHS0lJ7Y5KEHTt2lEzSMij7D2+4ON3Tqd9JqwLbRrEyJDJMxCY1PcYDtWuk69Rv3HaEY+vrMiTSdnhDdwx/4zed+rbvWsJ33DEZEmlzdAyHWs/fbkkC0tP9Sz9QAf7+x7Bz5zWd+tChnggP7y5DoucUinCDy5RK+cdO9H3btOlW3LyZpVN3c7PDxYsjZEikTfR8RJTH4MSpK1eu6H2CVM2aNZGTk4O4uLgSDfZPUN7mocG6UYevzZyD3eMi1Uubi3NGkeqlTV8TU1i9tCUnP9JbT0nRX6fnRN+3SmWO3npGhv56aRM9HxHlMdikXrp0qTRz/CM9zqmIShV1f+A+zqkIWxnylDUZWeXh6JCtvy5DnoLupDoUqV7aJEl/0yLK04tdXSvorVerpr9Oz4m+bxUKG2RmPtWpOzjYyJBGl+j5iCiP0ROnoqOjcf/+fYPLU1NTER0dbZJQ/xSZdp/h6VPtIX761AKZdp/JlKhsuZS2GE8KjN+Tpxa4lLZYpkTaJJc5iEtw0qrFJThBcpkjUyJtU6c2L1K9tIWEtIaHh/a1px4elRAS0lqmRM81aGBfpHppE33fhoX5wMpKu2O2spIQFib/tdqA+PmIKI/RE6ecnJywdu1avdeqAsCePXvw3nvvIS0tTe9yc3U34QdUynof5W0e4nFORWTafSbcpClAzGtSgbzJU02cguFg9xgZWeVxKW2xEJOm8n1/MBLqO3NR1TkDd1MdILnMEWLSVL4FC85i+fILUKvzjrJNnSrGxJp8CQmZmD8/BvHxqahTxxkhIa1lnzSVr+DkKVEmTeUTfd9GRychKCgSGRk5cHCwQViYj1CTkvLzpaU9hpNTeeHyEVERmlRHR0esW7fOYJO6bds2TJw4sdCjrSQuUZvUsoLjVzwcv1fHsSsejh+RuAp94lRmZiYyMp5PAklLS0NiYqLOekqlErt374arq6vpExIRERGR2Sm0Sf3888+xdOlSAHm3l5o5cyZmzpypd121Wo2PP/7Y9AmJiIiIyOwU2qR27doVtra2UKvVmDdvHgYPHowmTZporSNJEipUqIAWLVqgdWv5JzwQERERUdlXaJParl07tGvXDgCQk5ODfv36oVGjRqUSjIiIiIjMV6FN6ouCg4NLMgcRERERkYbBJnXr1q0AgOHDh0OSJM3rlxkxgo+UIyIiIqLiMdikTpgwAZIkwc/PD9bW1pgwYcJLNyZJEptUIiIiIio2g03q77//DgCwtrbWek1EREREVNIMNqlubm6FviYiIiIiKilGT5x60eXLlzU39a9VqxYaNWoESZJe8i4iIiIiIuMUqUndvXs35syZg6SkJK169erVMWfOHIOPTCUiIiIiKgqjm9QtW7Zg4sSJ8Pb2xty5c+Hl5QW1Wo1r165h8+bNCAwMxJMnTzBq1KiSzEtEREREZsDoJnXlypVo1aoVDh48CFtbW61l/v7+eOONN7By5Uo2qURERERUbBbGrnj79m0MHTpUp0EFAFtbWwwbNkznMgAiIiIioldhdJNav359JCcnG1yelJSEevXqmSQUEREREZk3o5vUefPmYdOmTdi7d6/Ost27d2Pz5s345JNPTBqOiIiIiMyT0dekhoaGwtnZGePGjUNwcDA8PDwgSRLi4+Nx7949eHp64r///S/++9//at4jSRJ27NhRIsGJiIiI6J/L6Cb1ypUrkCQJNWvWBADN9ac2NjaoWbMmcnJycPXqVa338N6pRERERPQqjG5SL126VJI5iIiIiIg0jL4mlYiIiIiotBTapK5fvx7x8fGa1yqVCleuXMHjx4911j1//jymT59u+oREREREZHYKbVKnT5+Oc+fOaV4rlUp06NABv/76q866sbGxWL9+vekTEhEREZHZKbRJVavVRtWIiIiIiEypTF2TumLFCigUCkybNk3uKERERERUgspMk3r27Fls2rQJjRo1kjtKkUi5CSif7o+K9/uifLo/pNwEuSNpsciOht2dpmheoRvs7jSFRXa03JG0fLNuPVLPekB1pRpSz3rgm3ViXVLy+af7cWBdN2T+MRwH1nXD55/ulzuSlmnTTkKhCNf8mjbtpNyRtERHJ6Fp063o1i0KTZtuRXS0OI9W7u+7GgfWdcO5fa1wYF039PddLXckLQsWnIWjYzjatDkBR8dwLFhwVu5IWvL3rZvbV8LtWwDYvTsO1atvRNu2J1C9+kbs3h0ndyQiKsDoW1DJKSMjA/7+/ggNDcXSpUvljmM0KTcBFdMGwvLZ9bzCU8DyaQweOu2D2spd3nD4X4OaPgAScvP+uaLKgl36AGQ5RkBl21HuePhm3Xr4954O63IqAICjQzb8XaYjfB0wOuA9mdPlNahD202Cl3uaphaXMAmffwpMmNRfvmD/M23aSYSH/6VVy3+9bFknOSJpiY5OwoAB3yE3N+8SoqysLAwY8B0iIt5Ax47VZc3W33c1NsxZrbVv2zVNQH9fYP/hf8uYLM+CBWexbNkFzWu1GprXs2a1kSfUCwru28zMp8LsWyCvQR037rjm9aNHuZrXfn5ecsUiogJeeiQ1JiYGe/fuxd69e3Hw4EFIkoTo6GhNLf/X2bMl96/4SZMmYcCAAfDx8SmxzygJtg/mP29Q/8fy2XXYPpgvUyJtFTKC8hrUF0jIRYWMIJkSafNtsUDToOazLqeCb4sFMiXSVqvCKq0mBgC83NNQq8IqmRJpK9igvqxe2oKCIjVNTL7cXDWCgiJlSvSc/6B9evet/6B98gQqYPnyC0WqlzaR9y0AfPBBVJHqRCSPlx5JXbduHdatW6dVW7Zsmd51S+IJU5s2bUJ8fDzWrl1r1PqxsbEmz/Cq6trGw1rPCGdnxSP2vvw5m1dI0/vPFHVumhDj6Gmve6szAFDYPxYiX/WqmfrrVTKFyFcYEfKlpenfv2lp8u9f0fetofmrajX3rTGys3MN1kXIl8/b21vuCESyKrRJPXDgQGnl0Cs2Nhbz5s3D4cOHYW1tbdR7RPpLbZteB8g+p1u3qwPvWvLnlO44Aaos3bqVkxDjmHq2PBwdsnXqygfl4d1G/nwHjlfSW0+6VwmtBBg/4ITBJSLsXyenGGRl6X7/nJzKy55P9H0rSSf0NqqSxH1rDFvbk3j0SLdRtbW1EiIfEeUp9HR/p06divzLlH799Vekpqaiffv2cHZ2hrOzM6Kjo7F+/Xo4OzsjJyfHpJ9natn2IXhm6aFVe2bpgWz7EJkSaXvkEAZ1gX+nqGGFRw5hMiXSdvj8LDx5qv0VffLUAofPz5IpkbbERx8iLsFJqxaX4ITERx/KlEibv3+DItVLW1iYD6ystM++WFlJCAuT/7Ke8L0D9e7b8L0D5QlUwNSpzYtUL20i71sACA3tXKQ6EclDUiqVwt74VKlUIilJe0bo+++/D09PT0yePBkNGjQokUsMTEnKTYDtg/mweJYClWU1ZNuHCDFpKp9FdjQqZARBnZsGycoJjxzChJg0le+bdevh22IBFPaPoXxQHofPzxJi0lS+zz/dj1oVVqF6lUwk3auExEcfCjFpKl/ByVP+/g2EmDSVLzo6CUFBkUhLewwnp/IIC/MRYmINkDd5yn/QPs2+Dd87UIhJU/kWLDiL5csvQK3OO4I6dWpzISZN5cvftxkZOXBwsBFq3wJ5k6c++CAK2dm5sLW1QmhoZ06aIhKM0E2qPn369EHDhg0NXhdLryY2NpanuYqB41c8HL9Xx7ErHo4fkbjKzH1SiYiIiMh8lIn7pL7o0KFDckcgIiIiohLGI6lEREREJBw2qUREREQknCI1qZmZmVi+fDn69++PDh06ICYmBgCQlpaG1atX49q1ayUSkoiIiIjMi9HXpCYlJeGNN97A7du34enpib///hsPHz4EADg5OWHz5s1ISkrCkiVLSiwsEREREZkHo5vU//znP8jMzERkZCRcXFzg5aV9P7k+ffrghx9+MHlAIiIiIjI/Rp/uP3r0KAIDA9GwYUO9N9CvXbu2zo33iYiIiIhehdFN6qNHj+Di4lLocpVKZZJQRERERGTejG5SPT09ce7cOYPLjx49ioYNG5okFBERERGZN6Ob1Lfffhvbtm3Dtm3bNEdMJUnCw4cP8fHHH+Pnn3/GuHHjSiwoEREREZkPoydOBQQE4K+//kJQUBDs7e0BAO+++y6USiWePXuGwMBADBs2rMSCEhEREZH5KNJjUVetWoXhw4dj7969iI+Ph0qlgoeHBwYPHoz27duXVEYiIiIiMjNFalIBoG3btmjbtm1JZCEiIiIiAsDHohIRERGRgAweSe3Xr1+RNyZJEvbv31+sQEREREREBptUlUql96b9hVGr1cUORERERERksEk9dOhQaeYgIiIiItLgNalEREREJByjZ/cnJiYWulySJNja2sLZ2bnIlwkQEREREb3I6Ca1adOmRjWftra26NixI6ZPn442bdoUKxwRERERmSejm9TQ0FCsW7cOiYmJGDJkCLy8vKBWq3Ht2jXs2rUL7u7uGDlyJK5du4YdO3agb9++2LdvH2/yT0RERERFZnSTmpaWhsePH+O3336Do6Oj1rLg4GD06tULOTk5WLJkCaZNmwYfHx8sXrwYERERJg9NRERERP9sRk+cCg8Px5gxY3QaVABwdnbGmDFjEB4eDgCoXLkyRo8ejfPnz5suKRERERGZDaOb1Hv37iE3N9fg8tzcXNy9e1fzunr16oWuby5sknvDPlmBSskK2CcrYJPcW+5IWmySu8I+WYFWFdv8L19XuSNp2bhiBOxuKVApSQG7WwpsXDFC7khaFs/bhQPruiHzj+E4sK4bFs/bJXckLbt3x6F69Y1wdg5H9eobsXt3nNyRtHx/MBKHN3THgz+G4/CG7vj+YKTckTRatdoChSJc86tVqy1yR9ISHZ2Epk23olu3KDRtuhXR0UlyR9KSn8/N7Suh84k6fkQESEql0qg78Pfo0QN37tzBkSNHUKNGDa1lt27dQu/evVGtWjUcPXoUABASEoKDBw/iwoULJg9dVtgk94YNzuDF6WZqADlohxzX7+WKpWGT3BU2uKAnX3PkuJ6QKdVzG1eMwL9HHMaL8/XUamD1Vl+MnbJVvmD/s3jeLozrOR1e7mmaWlyCEzb8sBTBs4fImCzP7t1xGDfuuE59w4Zu8PPzkiGRtu8PRqJV5bE643fu/kb07usjY7K8BvXatUc6dU/PCjh3bpQMibRFRydhwIDvkJv7/H/fVlYSIiLeQMeO1WVMlof5iMgUjG5ST58+DT8/P6jVavj6+qJOnToAgPj4eBw+fBhqtRp79+5F+/btkZ2djaZNm6JXr14IDQ0t0T+AyOyTFXoPVasAPHBVlnIaXaLns7ulgKWlbv3ZMyCrprLU8xR0YF03jO6ne0nLNwdaoF+AbnNY2qpX34hHj3TPZlSoYIWkpLEyJNJ2eEN3DH/jN536tu9awnfcMRkSPadQhBtcplT6l2IS/Zo23YqbN7N06m5udrh4Uf6zDcxHRKZg9MSp9u3b48iRI1i4cCG+//57PH78GABQvnx5dOvWDTNnzkSTJk0A5N2G6u+//y6ZxGWIoRt2iXIXWdHzWRi4GMVQvbRVr5qpv15Ff7205eTov9zGUL20uThnFKlOzymVOXrrGRn666WN+YjIFIxuUgGgSZMm2Lp1K1QqFe7duwcAqFKlCixE6RoEo4b+hs+oQ9elQPR8KhX0HklVqUo/iz5Jdyvpr9+rhFalnEUfGxsrvUdSbWyK9Ne+xNxJdShSnZ5TKGyQmflUp+7gYCNDGl3MR0Sm8ErdpYWFBVxcXODi4sIGtRBP0E6n4VP/ry6CJ2huIF9zGdLoCt3uC3WBgGp1Xl0Ef6S8j7gEJ61aXIIT/kh5X6ZE2kJDOxepXtoklzl6x09ymSNTouc8PSsUqV7awsJ8YGWl/U9MKysJYWHyXsubj/mIyBSMviYVAJRKJXbv3o0bN24gPT0d6gIdhCRJWLNmjclDlmU2yb1h/b/JU/kNqgiTpvLZJHeFNS5AUgNqKa9BFWHSVL6NK0bgg2GHYWGRdwQ1dLsYk6byLZ63C42qfYbqVTKRdK8S/kh5X4hJU/l2747DBx9EIScnFzY2VggN7SzEpKl83x+MhPrOXFR1zsDdVAdILnNknzSVr+DkKVEmTeWLjk5CUFAk0tIew8mpPMLCfISa9JOfLyMjBw4ONsLmE3X8iKgITWpkZCTeeustPHjwAPb29lAoFLobkyT8/vvvps5IpSA2Nhbe3t5yxyizOH7Fw/F7dRy74uH4EYnL6IvTPvroIzg6OuLQoUOaCVJERERERCXB6AtK4+LiEBQUxAaViIiIiEqc0U2qu7s7srOzSzILERERERGAIjSpkydPxsaNG5Genl6SeYiIiIiIjL8m9c6dO3ByckLLli0xaNAg1KxZE5YFbmIpSRL+7//+z+QhiYiIiMi8GN2k/uc//9H8fuPGjXrXYZNKRERERKZgdJPKW0sRERERUWkxukl1c3MryRxERERERBp8pikRERERCcfgkdS+ffvCwsICe/bsgZWVFfr16/fSjUmShP3795s0IBERERGZH4NNqlqthkql0rxWqVSQJKnQjanVRj1hlYiIiIioUAab1EOHDhX6moiIiIiopPCaVCIiIiISjtGz+wuKiorCjh07kJKSgrp162L8+PGoVauWKbMRERERkZkq9Ejq4sWLUaVKFdy5c0ervmXLFgwYMADffPMNjh49is8//xzdu3fHzZs3SzQsEREREZmHQpvUqKgodO/eHS4uLppaTk4OZs6ciUqVKiEiIgK3bt3Cl19+iaysLKxcubLEAxMRERHRP1+hTWp8fDxat26tVYuMjMSDBw8wceJEdOnSBRUrVsSgQYPw5ptv4sSJEyWZlYiIiIjMRKFNanp6OqpVq6ZVi4qKgiRJ6NWrl1a9efPmSElJMX1CIiIiIjI7hTapVatWRVJSklbt9OnTsLOzQ+PGjbU3ZGEBa2tr0yckIiIiIrNTaJPasmVLfPvtt1AqlQCAy5cv4/z58+jSpYvOjf2vXr2KGjVqlFhQIiIiIjIfhd6Catq0aejevTtatmyJ+vXr4/Lly5AkCf/+97+11lOr1Th48CC6d+9eomGJiIiIyDwUeiS1UaNGiIiIQOvWrXH//n289tpr2LNnD9q0aaO1XlRUFOzs7NC/f/8SDUtERERE5uGlN/Nv164dduzYUeg6Xbp0walTp0wWioiIiIjMm9CPRV25ciW6deuGWrVqwdPTE8OGDcOff/4pdywiIiIiKmFCN6knT57EuHHjcOTIEezfvx9WVlYYOHAg0tPT5Y5mNJsEBexvK1ApKe+/NgkKuSNpsbmel6tVxTZ5+a4r5I6kJT+fZvwEy/fTvpWwiKuKZravwSKuKn7aJ9YDLSK+XgKLuKqokOgIi7iqiPh6idyRtCQkZMLf/xjGjz8Pf/9jSEjIlDuSxs8/bEd6jAdUV6ohPcYDP/+wXe5IRERmRVIqlWq5QxgrKysLbm5u2LJlC3x9feWO81I2CQrYlANevBGCWg3kPAVy3JWy5cpnc10BGxs9+XKAHA+lbLnyiZ7vp30rMei1eTr59v46Gz0GTpYv2P9EfL0Eb/VYpJPv659mYsBbM+QL9j8JCZkYOPAwrl9/3ph6eFTCvn2+cHevJGOyvAa1V/0gWJdTaWpPnlrgyJUwdOk5TMZkumJjY+Ht7S13jDKL40ckLqGPpBaUlZUFlUoFhUIhdxSjWFtpN1hA3mvrl14JXDqsrQ3kE+R2t6Ln+1fjxXrz/avxYnkCFTCo/Qq9+Qa1XyFPoALmz4/RalAB4Pr1TMyfHyNToueaOAVrNagAYF1OhSZOwTIlIiIyP4K0S8YJDg5GkyZN8NprrxlcJzY2thQTFa5VRf11SRIjJ/MVTzPbp3rrtjZP8TvzvVR8/H0D9VTZ96+n3WO99Up2j2XPpo+ImcoSUcePR3jJ3JWZJvWjjz7CmTNn8P3338PS0tLgeiL9pVbf1j0SCOSdchUhJ/MVT3ZcOZSzeqJbzynHfEaoUycR585l6Kk7y54vPaY8HB2ydeqZWeXh3Vr+sXsRT1cXD8ePSFxl4nT/zJkzsXv3buzfvx+1a9eWO47RnuTmNVQvUqvz6iJ48sRAPt2+Rhai5/vxcrDefD9eFuOU8N7TU/Tm23t6ijyBCggJaQ0PD+1rTz08KiEkpLVMiZ67lLYYT55q/+/xyVMLXEoT41IOIiJzIPzEqRkzZmDPnj04ePAg6tWrJ3ecIrNJUGiuTc1vUEWYNJXP5rpCc+1nfgMowqSkfKLn+2nfSvyr8WLY2jxFdk45/Hg5WIhJU/kivl6CQe1XaPLtPT1FiElT+RIS8q5BjY9PRZ06zggJaS37pKl8P/+wHU2cguFg9xgZWeVxKW2xcJOmAB4JLC6OH5G4hG5Sp06diu3bt+Obb75B/fr1NfWKFSvCzs5OxmT/PPwfdfFw/IqH4/fqOHbFw/EjEpfQp/vXr1+PBw8eYMCAAahXr57mV2hoqNzRiIiIiKgECT1xSqlUyh2BiIiIiGQg9JFUIiIiIjJPbFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOGxSiYiIiEg4bFKJiIiISDhsUomIiIhIOFZyB/ins0luBWtcgwRADeAJPJHjek7uWBo2CTVgbfUQrSoC6tvAk9yKyHG/LXcsDZvk3rDGmRfGrx1yXL+XOxaZAYvsaFTICIKkUkJtocAjhzCobDvKHYuIyGzwSGoJskluBRtcgwUACXmDbYNrsEluJXOyPDYJNWBT7iEsLABJAiwsAJtyD2GTUEPuaADyGlQbnCkwfmdgk9xb5mT0T2eRHQ279AGwVN2EBTJhqboJu/QBsMiOljsaEZHZYJNagvKPoL5I+l9dBNZWDyEVCChJeXUR5B9BfZH0vzpRSaqQEQQJuVo1CbmokBEkUyIiIvPDJrUEFWywXlYvbQUb1JfVS5vo40f/XJJKaaCeUbpBiIjMGJvUEqQuYr20qQ0EMVQvbaKPH/1zqS0UBuoOpRuEiMiMsUktQU/gqdNQ5U+eEsGT3Io6DalanVcXwRO0MzB+7eSIQ2bkkUMY1AXmlaphhUcOYTIlIiIyP2xSS1CO6znkwBMq5DVXKgA5As3uz3G/jZynFaFS5TWnKhWQ81Sc2f05rt8jB+0KjB9n91PJU9l2RJZjBJ5ZuEEFBzyzcEOWYwRn9xMRlSLegqqE5TWq4spxv40cALGxsfD29pY7jo68RpWo9KlsOyLL9qLcMYiIzBaPpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDYpBIRERGRcNikEhEREZFw2KQSERERkXDKRJO6fv16NG3aFC4uLvDx8cGpU6fkjkREREREJUj4JnXPnj0IDg7GlClT8PPPP+O1117D0KFDkZiYKHc0IiIiIiohklKpVMsdojA9evRAo0aN8N///ldTa9myJQYMGIA5c+bImIyIiIiISorQR1KfPHmCCxcuoHv37lr17t2745dffpEpFRERERGVNKGb1NTUVDx79gxVqlTRqlepUgV3796VKRURERERlTShm9R8kiRpvVar1To1IiIiIvrnELpJdXZ2hqWlpc5R0/v37+scXSUiIiKifw6hm1Rra2s0b94cx48f16ofP34cbdu2lSkVEREREZU0K7kDvMz777+PwMBAtGrVCm3btsWXX36JlJQUjB07Vu5oRERERFRChD6SCgCDBw/GokWLsGzZMnTu3BlnzpzBjh074ObmplmHN/t/NStXrkS3bt1Qq1YteHp6YtiwYfjzzz/ljlUmrVixAgqFAtOmTZM7SpmRkpKC8ePHw9PTEy4uLmjbti1Onjwpd6wy4dmzZ5g/f77m/3tNmzbF/PnzkZubK3c0IUVHR2P48OFo0KABFAoFtmzZorVcrVZj0aJFqF+/PqpVq4Y+ffrgr7/+kiktEeUTvkkFgPfeew+XLl3C3bt3ERkZiY4dO2qW8Wb/r+7kyZMYN24cjhw5gv3798PKygoDBw5Eenq63NHKlLNnz2LTpk1o1KiR3FHKDKVSiV69ekGtVmPHjh345ZdfsHTpUl5rbqRPP/0U69evx5IlS/Drr79i8eLFCA8Px8qVK+WOJqSHDx+iYcOGWLx4McqXL6+zfPXq1fjss8+wZMkSHDt2DFWqVMGgQYPw4MEDGdISUT7hb+b/MrzZv+lkZWXBzc0NW7Zsga+vr9xxyoSMjAz4+Phg9erVWLp0KRo2bIhly5bJHUt48+bNQ3R0NI4cOSJ3lDJp2LBhcHR0xBdffKGpjR8/Hunp6di+fbuMycRXo0YNLF26FKNGjQKQdxS1fv368Pf3x9SpUwEAjx8/hre3Nz755BNeWkYkozJxJNUQ3uzftLKysqBSqaBQKOSOUmZMmjQJAwYMgI+Pj9xRypRDhw6hVatWGDt2LLy8vNCpUyesW7cOanWZ/jdzqWnXrh1OnjyJv//+GwBw5coVREVF4V//+pfMycqehIQE3LlzR+vnSPny5dGhQwf+HCGSmfATpwrDm/2bVnBwMJo0aYLXXntN7ihlwqZNmxAfH4+1a9fKHaXMuXHjBjZs2IAJEyZg0qRJuHTpEmbMmAEACAgIkDmd+CZNmoSsrCy0bdsWlpaWyM3NxdSpU/Hee+/JHa3MuXPnDgDo/TmSnJwsRyQi+p8y3aTm483+i++jjz7CmTNn8P3338PS0lLuOMKLjY3FvHnzcPjwYVhbW8sdp8xRqVRo0aKF5pKcZs2aIT4+HuvXr2eTaoQ9e/Zg27ZtWL9+PerXr49Lly4hODgYbm5uGDNmjNzxyiT+HCEST5luUnmzf9OYOXMm9uzZgwMHDqB27dpyxykTfv31V6SmpqJ9+/aa2rNnz3Dq1Cl8+eWXSEpKgo2NjYwJxebi4oJ69epp1erWrYtbt27JlKhsmT17NiZOnAg/Pz8AQKNGjZCYmIhVq1axSS0iFxcXAMDdu3dRs2ZNTZ0/R4jkV6avSeXN/otvxowZ2LVrF/bv34+6devKHafM6NOnD06dOoWoqCjNrxYtWsDPzw9RUVE8uvoS7dq1Q1xcnFYtLi4OtWrVkilR2fLo0SOdMx6WlpZQqVQyJSq73N3d4eLiovVzJDs7G6dPn+bPESKZlekjqQBv9l8cU6dOxfbt2/HNN99AoVBors2qWLEi7OzsZE4nNoVCoTPBrEKFCnB0dETDhg3lCVWGTJgwAT179sTy5csxePBgXLx4EevWrcPHH38sd7QyoXfv3vj000/h7u6O+vXr4+LFi/jss88wfPhwuaMJKSsrC/Hx8QDyLjW5desWLl68CEdHR9SqVQtBQUFYsWIFvL294eXlheXLl6NixYoYMmSIzMmJzFuZvwUVkHcz/9WrV+POnTto0KABFi5cqHUvVdLP0Cz+GTNmYObMmaUb5h+gT58+vAVVERw5cgTz5s1DXFwcatasCX9/fwQGBvI6QCM8ePAACxYswMGDB3H//n24uLjAz88P06dPh62trdzxhBMVFYV+/frp1EeMGIGwsDCo1WosXrwYX331FZRKJVq1aoXly5fzH5xEMvtHNKlERERE9M9Spq9JJSIiIqJ/JjapRERERCQcNqlEREREJBw2qUREREQkHDapRERERCQcNqlEREREJBw2qUQm1KRJEwQFBcny2VFRUVAoFIiKijLpdoOCgjSPjjQXffr0QZ8+feSOQURk1tikEhViy5YtmqdL5f/y9PSEr68vIiIi5I5XLA8ePMDy5cvh4+ODWrVqwcXFBa1bt8a0adNw7do1ueOVuNOnT2PRokVQKpVyRyEiIj3K/GNRiUpDcHAwPDw8oFarce/ePWzfvh1vv/021q9fXyYfnXjjxg0MGjQICQkJ6N+/P0aOHIny5cvj6tWr2LNnD7766ivcu3dP7pgl6syZM1iyZAlGjhyp8/S1vXv3yhOKiIg02KQSGaFHjx5o06aN5vU777yDevXqYdeuXWWuSc3NzcXo0aORkpKC/fv3o1OnTlrLP/74Y8ybN88kn6VWq5GTk1PmHtVpbW0tdwQiIrPH0/1Er8De3h4VKlRAuXLlCl3vyZMnWLBgAbp27Qp3d3dUq1YNPXr0wHfffaezrkKhwIcffogff/wRnTt3houLC1q2bIldu3bprBsbG4vBgwfD1dUVdevWxccff4ynT58alX3//v24fPkyJk+erNOgAoCtrS0WLlyoU7979y7Gjh2LWrVqwd3dHf/+97+RnZ2t98+wb98+dOjQAVWrVsXu3bsBAImJifD390edOnXg4uKCTp06YevWrVrvT0hIgEKhwKpVq7Bp0ya0aNECrq6u6NevH27cuAEAWLNmDZo0aYJq1arBz88PKSkpWts4deoU3nnnHTRu3BhVq1ZF/fr1MWnSJK3T+osWLcLcuXMBAM2aNdNcypF/PW/Ba1JfzLV161a0adMGVatWRYcOHXDixAmjxp2IiIqGR1KJjJCZmYnU1FQAwL179/Dll18iNTUVw4cPL/R9Dx48wMaNGzFo0CCMHj0ajx8/xs6dOzFq1Cjs2rULPXr00Fr/7NmzOHToEMaOHYu33noLmzdvRkBAAJo0aYJ69eppPr9Pnz54/Pgx3n//fTg5OWHbtm04fvy4UX+Ww4cPA8BLs79IpVJh0KBBaNSoEebOnYuYmBhs2rQJzs7OmD17tta6p0+fRkREBPz9/eHi4oK6desiNTUVvXv3Rnp6OgICAlCtWjXs2bMHQUFBUCqVOpPN9u7di8ePH+Pdd99FVlYWVq9ejVGjRsHPzw/79+/HhAkTkJKSgjVr1mDy5Mn49ttvtd6bnp6OMWPGwMXFBZcvX8bmzZvx119/4ciRIwCAfv36ITY2Fnv27MHChQvh7OwMAJoxNiQiIgKpqakYO3YsbG1tERYWhtGjR+PSpUtwdHQ0ejyJiOjl2KQSGcHPz0/rdbly5bBq1aqXzgBXKBT4448/YGNjo6kFBgaic+fOCA0N1WlSr1y5gujoaE2zNHDgQDRu3BjffPMNPvnkEwDAp59+irt37+K7775Dhw4dAORdfqDvqKg+V69eRaVKlVCrVi2j1geAp0+fwtfXFyEhIQCAd999F0qlEps2bdJpUq9evYrIyEg0bdpUUwsJCcHt27cREREBHx8fzTZ8fX0xf/58jBw5Eg4ODpr1b926hd9++01zraiFhQUWLVqE7OxsnDp1SjOeWVlZ+PLLL3H//n1UrlwZADB37lxUqFBBK1Pr1q0RGBiIM2fOoF27dmjcuDGaNGmCPXv2oE+fPnB3dzdqHK5fv45z585pPqtTp07o0qULdu3aBX9/f2OHk4iIjMDT/URGWLJkCfbt24d9+/Zh3bp16NatG6ZMmfLSGf6WlpaahurJkydIT0/HgwcP0LFjR1y4cEFn/c6dO2sdzatatSq8vb01p7oB4MiRI2jWrJmmQQWAChUq4J133jHqz/LgwQPY29sbte6Lxo0bp/W6Y8eOSE1NxYMHD7Tqbdu21WpQ8zM3bdpU06ACedd9BgUF4eHDhzh58qTW+v3799eazNS6dWsAwJAhQ7Qa/latWkGtViMhIUFTy29Q1Wq15gh427ZtAUDvmBfFwIEDNQ0qADRt2hSVKlXS2j9ERGQaPJJKZISWLVtqTZwaMmQIfHx8MH36dPj6+hY60Wbz5s34/PPPcfXqVajVak1dkiSddfUd3VQoFEhPT9e8TkxMRL9+/XTW8/LyMurPYm9vX+Smqly5cnB1ddXJBQDp6elaTW/t2rV13n/z5k29mfMb8ps3b2rVa9asqfW6UqVKAIAaNWrorb94vemtW7cwe/Zs/PjjjzoNdEZGhk6GotC3fxwcHLT2DxERmQaPpBK9AgsLC3Tq1Al37twp9J6iu3btwv/93//Bw8MDn3/+OXbt2oV9+/Zh6NChWg1rPktLS73bKbiuvgZX3/b0qVevHjIzM3Hr1i2j1gfy/ryGFPzc8uXLG71dQ5kNjcPLxkelUmHw4ME4ceIEPvzwQ3zzzTfYu3evZvKWSqUyOturfD4REZkOj6QSvaLc3FwAwMOHDw2us2fPHtSuXRvffvutVmO5ZcuWV/7cWrVq4e+//9apG3sDfl9fX+zcuRPbtm3D1KlTXzlHUbi5uenNHBsbq1luCpcvX8bff/+Nzz//HCNHjtTU9Y2NvkafiIjEwSOpRK/g6dOnOH78OKytrVG3bl2D6+UfeXvxSNuNGzdw8ODBV/7snj174vfff8epU6c0tUePHuGrr74y6v39+/dH48aNsXLlSpw+fVpneU5ODmbNmvXK+fTp1asXLl68iJ9//llTe/r0Kb744gtUqFDB6ElfL6NvvAEgNDRUZ938a1f5xCkiIjHxSCqREX766SfEx8cDyLsF1J49exAXF4cPP/xQc12kPr6+vjhw4ABGjBgBX19fJCUlYcOGDfD09MTly5dfKcukSZOwY8cODB8+HAEBAZpbUBWc0W6IlZUVvvnmGwwcOBB9+/ZF//790aFDB9jY2CAuLg579uzB3bt3sWDBglfKp8+HH36IPXv2YMSIEQgMDISLiwv27t2Ls2fPYuHChVoz+4ujbt268PT0REhICJKSkuDo6Igff/wRSUlJOuu2aNECAPDJJ5/Az88P1tbW6NKlC6pUqWKSLEREVDxsUomMsHjxYs3vbW1t4e3tjZUrV2Ls2LGFvm/kyJG4f/8+NmzYgBMnTqBOnTpYuHAh4uPjX7lJrVq1Kg4dOoQZM2ZgzZo1sLe3x7Bhw9C9e3cMHjzYqG3Url0bP//8M9auXYv9+/fjhx9+QG5uLmrVqoU+ffro3Le0uJydnXHkyBHMnTsXGzduxKNHj+Dl5YWwsDCMGDHCZJ9Trlw5bNu2DcHBwQgNDYWFhQVef/117N69W+eId5s2bRASEoKvvvoK77//PlQqFQ4cOMAmlYhIEJJSqeQV/0REREQkFF6TSkRERETCYZNKRERERMJhk0pEREREwmGTSkRERETCYZNKRERERMJhk0pEREREwmGTSkRERETCYZNKRERERMJhk0pEREREwvl/nVOw+wdtqcEAAAAASUVORK5CYII=\n", "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "\n", "pwc_darkblue = patients_with_colors[patients_with_colors['Color'] == 'darkblue']\n", "pwc_gold = patients_with_colors[patients_with_colors['Color'] == 'gold']\n", "\n", "fig, ax = plt.subplots(figsize=(7,6))\n", "\n", "ax.scatter(pwc_darkblue['Bland Chromatin'], \n", " pwc_darkblue['Single Epithelial Cell Size'], \n", " label='Color=darkblue', \n", " color='darkblue')\n", "\n", "ax.scatter(pwc_gold['Bland Chromatin'], \n", " pwc_gold['Single Epithelial Cell Size'], \n", " label='Color=gold', \n", " color='gold')\n", "\n", "x_label = 'Bland Chromatin'\n", "\n", "y_label = 'Single Epithelial Cell Size'\n", "\n", "plt.ylabel(y_label)\n", "\n", "plt.xlabel(x_label)\n", "\n", "ax.legend(bbox_to_anchor=(1.04,1), loc=\"upper left\")\n", "\n", "plt.xlim(0, 11)\n", "plt.ylim(0, 11);\n", "\n", "plt.show()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Oops. That plot is utterly misleading, because there are a bunch of points that have identical values for both the x- and y-coordinates. To make it easier to see all the data points, I'm going to add a little bit of random jitter to the x- and y-values. Here's how that looks:" ] }, { "cell_type": "code", "execution_count": 11, "metadata": { "tags": [ "remove_input" ] }, "outputs": [ { "data": { "text/html": [ "
\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "
Bland Chromatin (jittered)Single Epithelial Cell Size (jittered)ClassColor
02.8921691.9601920gold
12.8876527.0179600gold
23.1446262.2157010gold
32.9998733.1970080gold
43.0255121.9855260gold
\n", "
" ], "text/plain": [ " Bland Chromatin (jittered) Single Epithelial Cell Size (jittered) Class \\\n", "0 2.892169 1.960192 0 \n", "1 2.887652 7.017960 0 \n", "2 3.144626 2.215701 0 \n", "3 2.999873 3.197008 0 \n", "4 3.025512 1.985526 0 \n", "\n", " Color \n", "0 gold \n", "1 gold \n", "2 gold \n", "3 gold \n", "4 gold " ] }, "execution_count": 11, "metadata": {}, "output_type": "execute_result" } ], "source": [ "def randomize_column(a):\n", " return a + np.random.normal(0.0, 0.09, size=len(a))\n", "\n", "jittered = pd.DataFrame(\n", " {'Bland Chromatin (jittered)':randomize_column(patients['Bland Chromatin']),\n", " 'Single Epithelial Cell Size (jittered)':randomize_column(patients['Single Epithelial Cell Size']),\n", " 'Class':patients['Class']})\n", "\n", "\n", "jwc = pd.merge(jittered, color_table, on='Class')\n", "\n", "jwc.head()\n" ] }, { "cell_type": "code", "execution_count": 12, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAqkAAAGTCAYAAAALL4uRAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAACEVElEQVR4nO3deVhUZf8G8HsYQBAhEBFQdETAfY9et1zzl5KoqKGZLVrhUrZo5fI2aQul2GK+amqaZWWLlqK4lrnkmmKWWxoKjrIpIsgiCLP8/qAZGebMMMDMnIPcn+vquuI5Z858PTMw9zzneZ4jy83N1YGIiIiISEKcxC6AiIiIiKgihlQiIiIikhyGVCIiIiKSHIZUIiIiIpIchlQiIiIikhyGVCIiIiKSHIZUIiIiIpIchlQCACQlJYldQq3G81czPH/Vx3NXMzx/RNLFkEpEREREksOQSkRERESSw5BKRERERJLDkEpEREREkuMsdgFEREQkHrVajcLCQrHLoDrIw8MDzs7moyhDKhERUR2lVquRn58Pb29vyGQyscuhOkSn0yE3Nxeenp5mgyov9xMREdVRhYWFDKgkCplMBm9vb4u9+AypREREdRgDKomlsvceQyoRERERSQ5DKhERERFJDkMqEREREUkOQyoRERHVSevWrUPTpk3FLgMAsGTJEnTs2LHGxzlw4AC8vb2RnZ0tuF2lUsHb2xsnT540ewxr9nEEhlQiIiKqla5fv45Zs2ahS5cuaNy4Mdq2bYtHH30UP//8s9ilkQ1wnVQiIiKqdVQqFYYMGYIGDRpg3rx56NChA7RaLfbv348ZM2bgzJkzDqmjpKQErq6uDnmuypSUlIhdgk2xJ5WIiIhqRKXKQ0zMHkRGbkVMzB6oVHl2f87XXnsNOp0Oe/fuxciRIxEWFobWrVtj0qRJOHjwIADg6tWrGD9+PIKCghAUFIQnnngCaWlpFo/7xRdfoGvXrvDz80PXrl2xdu1ao+3e3t5YtWoVnnjiCTRp0gTvvPNOtepfvHgxWrVqhaZNm2Ly5MkoKCgw2v7HH39g5MiRaNmyJZo1a4YhQ4bg2LFjVa7lzp07GD9+PPr27YusrCxD+8WLFzFkyBD4+/vjgQcewJ49e8zWKjSEQGhIwPnz5zFmzBgEBQUhNDQUzz77LK5du1blc6PHkEpERETVplLlISpqBzZsuISDBzOwYcMlREXtsGtQzcnJwe7duxETE4MGDRqYbPf29oZOp8P48eORlZWFLVu2ICEhAZmZmRg/fjx0Op3gcRMSEvD6669j6tSpOHLkCKZMmYJXX30VO3bsMNovLi4ODz/8MA4fPoznnnsOANC0aVOL/z366KOGx2/atAmxsbGYM2cO9u/fj7CwMHz66adGz5Gfn4+xY8dix44d+PXXX9GxY0dER0ebjDUVqkUvLy8Po0ePRk5ODrZu3Qo/Pz/Dtnnz5mHy5Mk4cOAA+vfvj8cffxzp6elWnH1hmZmZeOSRR9C2bVv8+uuviI+PR0FBAcaNGwetVlutY/JyPxEREVVbbGwiUlKMA2lKSh5iYxOxatVAuzxncnIydDodWrVqZXafffv24cyZMzh58iQUCgUAYPXq1ejatSv279+P/v37mzxm6dKlGDt2LCZNmgQACA0NxZ9//onFixcjIiLCsN/IkSPx1FNPGT32wIEDFmt2c3Mz/P/y5csxbtw4TJw4EUBZr/CBAweQnJxs2Kdfv35Gj1+4cCG2bNmC3bt3Y+zYsWZruXr1KgDgxo0bmDRpEgIDA/Hll18aPT8APPPMMxg5ciSAsqC7Z88erFmzBkql0uK/w5zPP/8cHTp0wNtvv21oW7lyJVq0aIGTJ0/i/vvvr/IxGVKJiIio2jIybgu2Z2YKt9uCuZ7Q8i5cuIDAwEBDQAWAFi1aIDAwEOfPnxcMqRcuXMD48eON2nr27GnSk9q1a1eTx7Zs2dLK6sue58knnzRqe+CBB4xCalZWFt577z0cOHAAWVlZ0Gg0KCoqQmpqaqW1AMCoUaPQqVMnfP3113B2No17DzzwgOH/nZyccP/99+P8+fNW/xsq+uuvv3D48GHB1RJSUlIYUomIiMixAgPrC7YHBAi320JISAhkMhn++ecfs/vodDqzt920dDtOoW0V2zw8PEz2qWwpq549e+LHH3+0uE95U6dOxfXr1/H++++jefPmqFevHoYPH24yOUqoFgAYPHgwNm3ahLNnz6Jz585WP68QJ6ey0aHlvxyo1WqjfbRaLR5++GHExsaaPL78MIOqYEglIiKialMqw5GYmGV0yT842AtKZbjdntPHxwcPPfQQVq1ahcmTJ5uMS83NzUWbNm2Qnp4OlUpl6E29fPkyMjIy0KZNG8Hjtm7dGkePHjXq5Txy5IjZ/curyuX+1q1bIzEx0eh5EhMTjfY/evQoFixYgMGDBwMoW26rKpOQ3njjDfj4+CAqKgqbN29Gp06djLYnJiYahhTodDr88ccfGDFihOCxGjVqBKBs3Kn+/0+fPm20T+fOnbFp0yY0a9YMLi4uVtdpCUMqERERVZtC4YX4+AjExiYiM/M2AgLqQ6kMh0LhZdfn/fDDDzF48GAMGDAAb7zxBtq3bw+dTocDBw5g0aJFOH36NDp06IBJkyYhLi4OOp0OM2fOROfOndG3b1/BY7744ouYMGECunTpgoEDB2L37t3YsGEDvv7660rrqcrl/ilTpmDKlCno1q0bHnzwQWzevBknTpyAt7e3YZ+QkBCsX78e4eHhuH37NubOnVvlpa7efPNN6HQ6Q1Atf7OANWvWIDQ0FO3atcPq1atx9epVPPPMM2b/bUFBQViwYAHeeustXLlyBR988IHRPs899xzWrl2LiRMn4pVXXkGjRo1w+fJlwyQxT0/PKtUOMKTahUytglt+LJw0GdDKA1HsqYTOWVH5A4mIqkGlKpukkpFxG4GBjgkI9yKex+pTKLzsNknKnBYtWmD//v346KOPMG/ePGRkZKBhw4bo0KEDFi1aBJlMhnXr1mHWrFmIjIwEUDYZaeHChWYv90dGRmLhwoVYsmQJ5syZg2bNmuGjjz4ymjRlC6NGjcLly5fx7rvvoqioCBEREXj++efx7bffGvZZunQpXnnlFfTv3x8BAQGYPXu22btIWTJ37lzodDqMGDECmzdvhpdX2Xt63rx5WLZsGf766y80a9YM33zzjdkhCy4uLvj888/x6quv4sEHH0THjh0xd+5cowlcgYGB2LVrF95++22MHj0ad+7cQVBQEAYMGIB69epVuW4AkOXm5lY++pisJlOr4HEzCnJNiqFNIw9GYcN4SQfVpKQkhIWFiV1GrcXzVzO18fxJIdCoVHl48cVfcOzYLRQXawztwcFlPVsMWJXTv/f0yyhVvGR9r5/HW7du4b777hO7DKrDLL0HuU6qjbnlxxoFVACQa1Lglm86kJjuLWIsZk3iEGNdSHM1/PbbTaOACtxd/kdstel3wtIySkQkDl7utzEnTYaZ9kwHV0KOlJZWhOnTjXthEhOz7vlemLpKjHUhramhPHsu/2MNoZ5Jqf1OqFR5ePPNcygouIALF3IE9xH7PBLVZQypNqaVBwKlQu0Bji+GHGbFihTRQwvZT8VL+8nJwuHQkYHG3NqUevZc/kfP0pAHKQR5c1SqPMyZcwS7d6eipMTynXAccR6JSJioIfXQoUNYsmQJ/vrrL2RkZGDZsmVGi+jqdDosWLAAa9euRW5uLu6//358+OGHaNu2rYhVW1bsqYS8NNFkTGqxZ/Xu4FBXlP+w8/JygU6nw/XrxcjKKkLjxu6G5Uyk0AMj9MGclXVHcF8p9cJIYQxlbSTUI+jhIfyn05GBxtzalAAQFORh1+V/gMp7SsVY4N0aQnWb4+YmR0FBCVSqPP6uEIlA1JBaWFiIdu3aYdy4cZgyZYrJ9sWLF2PZsmVYtmwZwsLCsHDhQowcORLHjx+v1lIGjqBzVqCwYfy/s/szoZUHcHZ/JSr70LhypQCJiVmSuFRo7oO5WTPhNeGk0gtTGy69SpVQj2BhoRoeHs4oLLy7mLW914WsSKkMx/btKqMa9Dp2bGj317WynlIxFni3RmXDJFxdneDkJENxsQbFxRrs2HEV58/v4O8KkQhEnTj18MMPY+7cuRgxYoThbgZ6Op0Oy5cvxyuvvIIRI0agXbt2WL58OQoKCqp0xwYx6JwVKPJZhcJGCSjyWVVrAqpYkxwq+9DQk8IkBnMfzIAOwcHGH2CODi2WcFKIeZW97831CLZr1xDR0SHo0ycQ0dEhDg8xCoUX2rTxEdxWUGAaXG2tsp5SpTLc5HfCw8MZEyZUvii6PVU2TEImg2QnohHVNZIdk6pSqXDt2jUMHHh37JK7uzt69eqF33//HRMnThR8XFJSkqNKvKekpRVh2rTNSE0tNrQdOZKGpUs7o2lTd7s+d3LyjSrsmy3qa2yu1sJCLRYtaosVK1KQlVUCPz9XTJkSjJKSa0hKsv4OIbaWllaEFStScPCg8Np6Yp/P8sSoo+x9/5fF972TU4mZR5dg5sxmd38S4bX28zN3y8c7dj+fDRpoBNs9PDSG5541KxjTp59GUVHZuM/CQjUmT/7VIX9XzDFXt169ejLcERi9I8bvSm1blo3I1qwKqSkpKdi6dSuOHj2Kf/75B9nZ2ZDJZPD19UWrVq3QvXt3PPLIIwgJCbFZYfpbf1W836ufnx8yMoRn0AP8pa6uN980DqgAkJpajHXrbth9kkPLlldx4sQtK/f1FfU1Nlern58r+vfvhP79Owk8ShwqVZ7JigMViX0+9cRaJ3Xhwj2Vvu89PC4BMA35p0/nwdXVX7RLwCpVHpyckuHiIkNpqfFy18nJd+xeW1ycPy5cMF1XNC5ugOF5Fy7cYwioeo76u2KOUN16QUEe6NTJF9u3XzHZJpXfFaK6xOLl/p07d+KRRx7B/fffj7lz5+Lvv/9Gs2bNMGDAAPTr1w9BQUE4e/Ys5s6diwceeAARERHYsWOHTQuseFcInU5n9k4RVH1iTvwRuiwoJCjIAwUFJaKuuShUa3CwF6ZMCXZ4LZWpbBiFIybXSJ01k3vy84UvnRcXa0W7BKwfY7x9+xWTgAoAqamFdq9NfytMS0MepDh5qnzdDzzQGIGB9RAe7ofo6BBs2xaJ+fN7SnroDlFdYrYnddCgQTh9+jSGDBmCL774Av369TO6p2x5ubm52LNnDzZv3owJEyagU6dO+OWXX2pUmL+/PwDg+vXrCAoKMrTfuHHDpHeVas7PT/iWZY6Y5FDxvs+enmWz+7OyipGeXmgYH3bjRhF27LhqeJwYE3/M3aO6pOTuZV6pzKKvbOydIybXSJ01k3sszaIXK2xZM47bEbVVditMqU6eKl+3UC++GPehJ3GsW7cOM2fORFpamtilVIu3tzfWrl2LESNGCG7Pzs5GSEgIEhIS0KdPHwdXV3NmQ2rPnj3xzTffICCg8vU9vb29MWrUKIwaNQoZGRn49NNPa1yYQqGAv78/9u7di27dugEAiouLceTIEbzzzjs1Pj4ZmzIlGBcuFJtcunNU74HQh52+tyg9XfjDVqw1F4Vq1Y9FlNIsekvhCnDM5BqpUyrDkZiYZfF9b2kWvVhhq7IvIID4QRCw7vxKkRj3oafquX79Oj766CPs2rUL6enp8PX1Rfv27TFp0iQ8/PDDYpdHNWQ2pL777rvVOmBgYKDVjy0oKEBycjIAQKvVIjU1FadOnYKPjw+aNWuGqVOn4qOPPkJYWBhCQ0Px4YcfwsPDA48++mi1aiPzmjZ1l1zvgVR6i6pCSguYCwWE8qQQYsRmrme8/PteofDC+vWDMWbMLlGXnCqvsi8gUgmC1pxfoupSqVQYMmQIGjRogHnz5qFDhw7QarXYv38/ZsyYgTNnzjikjpKSEri6ujrkueoaUWf3nzx5EsOGDTP8PH/+fMyfPx/jxo3D8uXL8fLLL6OoqAivv/66YTH/jRs3SnaN1NpOar0HtaW3qDwpjcHTB4Q5c45gz540o2V1pBJipMCa933v3k1w+PBoyYQtoS8gHh7OaNvWR1I3vgCk93eF7EOmVv27PngGtPJAh6wP/tprr0Gn02Hv3r1o0KCBob1169YYM2YMAODq1auYPXs29u/fDwDo378/4uLi0LRpU7PH/eKLL/C///0PqampCAoKwiuvvIKnn37asN3b2xsffPAB9u/fjz179uCZZ55BbGxslev/+OOPsXz5cty+fRuRkZEIDg7GunXrcPr0aQBlnXcffvgh1q5di6ysLISGhuKNN97A0KFDzR7zjz/+wPTp03H+/Hm0atUKSmXtvpGQ2ZD63XffVeuA48aNs3rfPn36IDc31+x2mUyGOXPmYM6cOdWqhWq32tJbVJ7UxuApFF749tvBhnGyUghYtZWUwlb5Hsrk5Gy0bOnL15REI1Or4HEz6u6dFksBeWkiChvG2y2o5uTkYPfu3VAqlUYBVc/b2xs6nQ7jx4+Hm5sbtmzZAplMhtdffx3jx4/H3r17BSdhJyQk4PXXX8f777+PgQMH4tdff8Wrr76Kxo0bIyIiwrBfXFwc5s6daxROLQVfoGwYpX6d959++glxcXH44IMP0KtXL2zZsgWffPIJ7rvvPsP+y5cvx5IlS/Dxxx+ja9eu+OGHH/Dkk09i37596NTJdCWZwsJCjBkzBr1798by5cuRkZFR6/OT2ZD6/PPPm7TpX1CdTifYDlQtpBJZYq63qF27hmjRwlOSH8pSHYMnpYBFtqF/TcVavotIzy0/1uhW4AAg16TALT8WRT6r7PKcycnJ0Ol0aNWqldl99u3bhzNnzuDkyZNQKMrC8urVq9G1a1fs378f/fv3N3nM0qVLMXbsWEyaNAkAEBoaij///BOLFy82CqkjR47EU089ZfTYAwcOWKzZzc3N8P8rVqzA448/bjjGjBkzcODAAVy8eNGolmnTpiE6OhoA8MYbb+Dw4cNYunQpPvvsM5Pjb9iwASUlJVi2bBkaNGiAdu3a4dVXX8XkyZMt1iVlZkPqX3/9ZfRzfn4+pkyZAk9PT0yePBmhoaHQ6XS4ePEiVq5cicLCQqxYscLuBVPdURvHs9XGmomIasJJI7x2uZMm027PWbGzTMiFCxcQGBhoCKgA0KJFCwQGBuL8+fOCIfXChQsYP368UVvPnj1Nltfs2rWryWNbtmxpZfXAP//8YxJy77//fkNIzcvLQ0ZGBnr06GFSy88//yx4zAsXLqB9+/ZGPcv/+c9/rK5JisyG1ObNmxv9/NJLL8HHxwebN2826jnt0KEDhg8fjhEjRmDlypVYvHix/aqlOqc29gDWxpqJiKpLKw8ESoXaK18dqLpCQkIgk8nwzz//mN3H0rrqltZbF9pWsc3Dw8Nkn6pc7q+sBkvMPc6a4F7bWFzMv7yEhAQMGzZM8OQ4OTlh+PDhSEhIsGlxREREJG3Fnkpo5MY3NNHIg1Hsab9JOz4+PnjooYewatUqFBQUmGzPzc1FmzZtkJ6eDpVKZWi/fPkyMjIy0KZNG8Hjtm7dGkePHjVqO3LkiNn9yztw4IDF//73v/8Z9m3VqhX++OMPo8eX/9nLywuBgYGCtbRu3Vrw+du0aYNz586hsLDQ0Hb8+PFK65Yyq2f3q9VqXLlieqs4vcuXL6O0VOCrFBEREd2zdM4KFDaM/3d2fya08gCHzO7/8MMPMXjwYAwYMABvvPEG2rdvD51OhwMHDmDRokU4ffo0OnTogEmTJiEuLg46nQ4zZ85E586d0bdvX8Fjvvjii5gwYQK6dOmCgQMHYvfu3diwYQO+/vrrSuupyuX+KVOm4IUXXkDXrl3Rq1cvbN26FYmJiUY3TXrxxRcxf/58hISEoEuXLvjhhx9w5MgR7Nu3T/CYjz76KN59911MmzYNM2fORGZmJj766COra5Iiq0PqwIED8dlnn6FTp0549NFHjSZRbdiwAatXrzYaVExERER1g85ZYbdJUua0aNEC+/fvx0cffYR58+YhIyMDDRs2RIcOHbBo0SLIZDKsW7cOs2bNQmRkJACgX79+WLhwodlL5pGRkVi4cCGWLFmCOXPmoFmzZvjoo49snm9Gjx6Ny5cv4+2330ZRUREiIyPxzDPPYPv27YZ9pkyZgoKCAsybNw/Xr19HWFgYvvrqK8GZ/QDQoEED/PDDD5gxYwb69euHsLAwvPXWW7V6QrssNzfXqkEM165dw/Dhw5GUlAQ/Pz8EBwdDJpMhOTnZcPK2bNli1R2qSHo4Q7hmeP5qhuev+njuaqaun79bt24ZLXtE4hk/fjzUajV++OEHsUtxKEvvQat7Uv39/fHbb7/hyy+/xM8//4yrV69Cp9OhQ4cOePjhh/H0008bLa9ARERERKZu376Nzz//HIMGDYKzszO2bNmC7du346uvvhK7NEmp0h2n6tWrh8mTJ9fqNbeIiIiIxCSTybB79258/PHHKC4uRsuWLbFy5Uqju3BSNW6LWlRUhJMnTyIrKwu9e/dGo0aN7FEXERER0T3J3d0dmzdvFrsMybN6CSqg7A4JrVu3xtChQzFx4kScPXsWAJCdnY3mzZuzm5qIiIiIbMLqkLpu3TrMmTMHgwYNwtKlS40WjfX19cWAAQOwadMmuxRJRERERHWL1SF12bJlGDx4MNasWSO4FEOXLl1w4cIFmxZHRERE9nUv3qmIaofK3ntWh9RLly5h8ODBZrf7+voiOzvb+sqIiIhIVB4eHsjNzWVQJYfT6XTIzc0VvMWsntUTpzw9PXHr1i2z2y9dusRJVERERLWIs7MzPD09kZeXJ3YpVAd5enrC2dl8FLU6pPbt2xfr1q3D1KlTTbalpaVh7dq1GDFiRPWqJCIiIlE4OztzQX+SJKsv9yuVSty4cQP9+/fHqlWrIJPJ8Msvv+Ctt95C79694eLigpkzZ9qzViIiIiKqI6wOqS1btsTOnTsREBCAuLg46HQ6LFu2DIsXL0bnzp2xc+dONG3a1J61EhGRGSpVHmJi9iAycitiYvZApeLlWyKq3ay63K/VapGWlobGjRtj06ZNyM3NRXJyMrRaLVq0aMGxqER0T1Kp8hAbm4iMjNsIDKwPpTIcCoWX2GWZUKnyEBW1Aykpd4NpYmIW4uMjJFkvEZE1rOpJ1Wg06Nq1K9atWwcA8Pb2Rrdu3RAeHs6ASkT3JH3w27DhEg4ezMCGDZcQFbVDkj2UsbGJRgEVAFJSygI2EVFtZVVIdXFxQUBAAGQymb3rISKShNoU/DIybgu2Z2YKtxMR1QZWj0l96qmn8O2336K4uNie9RARSUJtCn6BgfUF2wMChNuJiGoDq5egCg4Ohk6nwwMPPIBx48ahRYsWcHd3N9lv5MiRNi2QiEgMtSn4KZXhSEzMMur5DQ72glIZLmJVREQ1Y3VInTRpkuH/P/jgA8F9ZDIZQyoR3RNqU/BTKLwQHx+B2NhEZGbeRkCAdCd5ERFZy+qQmpCQYM86iIgkpbYFP4XCC6tWDRS7DCIim7E6pD744IP2rIOISHIY/IiIxGN1SNUrKirCyZMnkZWVhd69e3MJKiIiIiKyOatn9wPAihUr0Lp1a0RGRmLixIk4e/YsACA7OxvNmzfHV199ZZciiYiIiKhusTqkrlu3DnPmzMGgQYOwZMkS6HQ6wzZfX18MGDAAmzZtskuRRERERFS3WB1Sly1bhsGDB2PNmjWIiIgw2d6lSxdcuHDBpsURERERUd1kdUi9dOkSBg8ebHa7r68vsrOzbVIUEREREdVtVodUT09P3Lp1y+z2S5cucRIVEREREdmE1SG1b9++WLduHe7cuWOyLS0tDWvXrsWgQYNsWhwRERER1U1Wh1SlUokbN26gf//+WLVqFWQyGX755Re89dZb6N27N1xcXDBz5kx71kpEREREdYTVIbVly5bYuXMnAgICEBcXB51Oh2XLlmHx4sXo3Lkzdu7ciaZNm9qzViIiIiKqI6q0mH/r1q2xadMm5ObmIjk5GVqtFi1atOBYVCIiIiKyKat7UuPi4nDu3DkAgLe3N7p164bw8HBDQP37778RFxdnnyqJiIiIqE6xOqQuWLDAcIcpIQypRERERGQrVbotqiUFBQVwcXGx1eGIiIiIqA6zOCb1zJkzOH36tOHnI0eOQK1Wm+yXm5uLNWvWIDQ01PYVEhEREVGdYzGkbt261XAJXyaT4YsvvsAXX3whuK+npydWrVpl+wqJiIiIqM6xGFKfeuopDBo0CDqdDg8//DBmz56Nhx56yGgfmUyG+vXrIyQkBK6urnYtloiIiIjqBoshtUmTJmjSpAkAICEhAW3atOFyU0RERERkd1ZPnHrhhRdw7Ngxs9t37tyJzp0726QoIiIiIqrbrA6pV65cQWFhodnthYWFuHr1qk2KIiIiIqK6rUpLUMlkMrPbLl68CE9PzxoXRERERERkcUzqt99+i++++87w84cffoi1a9ea7Jebm4tz585h8ODBtq+QiIiIiOociyG1sLAQ165dM/x869YtaLVao330s/uffvppzJ492z5VEkmMSpWH2NhEZGTcRmBgfYwf3whhYWJXRUREdO+wGFJjYmIQExMDAOjUqRMWLFiARx55xCGFEUmVSpWHqKgdSEnJM7QdOZKGbdtaQKHwErEyUxXDtFIZLrkaiYiIhFgMqeWdOnXKnnUQ1RqxsYlGARUAUlOLERubiFWrBopUlSmhMJ2YmIX4+AgGVSIikjyrQyoRlcnIuC3Ynpkp3G4P1vSQ6sO0omk2Yl/ehSaN85B+3Qsrl2rx/gfjHFYrERFRdZgNqT4+PnByckJGRgZcXV3h4+NjcXY/UDY+NTs72+ZFUt1QWy5NBwbWF2wPCBButzVrekhVqjzs25cGRdNs7P78M4Qqbhr27X99HmTqXtA5KxxSLxERUXWYDakzZ86ETCaDs7Oz0c+OpNFoMH/+fKxfvx7Xrl2Dv78/xowZg9mzZxvqontDbbo0rVSGIzExy6jWoCA3KJXhDnl+oeEGKSl5huEG+nOZlVWMrxfuMgqoABDU+DpK8mNR5LPKIfXeC2rLFygionuJ2aQ3Z84ciz87wieffILVq1dj+fLlaNeuHc6ePYupU6fC1dUVM2fOdHg9ZD+Wgtfq5SFwy4+FkyYDWnkgij2VovYCKhReiI+PQGxsIjIzbyMgoGx2v6NCS2XDDcqfyyaN8wT3ddJk2qe4e4Q+lKak5CEtrQA3btxBaendlU2OHMnEtm2RDKpERHYk6e7IY8eOYciQIYiIiAAAKBQKRERE4MSJEyJXRrZmLnih9DI8br4KuSbl35+B61f2Y/43b2PytKGihQSFwstoklRSUpLRdnv2vFU23KD8uUy/LvycWnmATWq5Fwn16leUmlqIOXOO4NtvxVkbuvz7q0EDDeLi/BmYieieYzakHjp0CADQu3dvo58rPaCzM3x9fREaGlrj4nr06IHPP/8c//zzD1q1aoXz58/jwIEDmD59eo2PTdJiLni9+NimuwH1X0GNr6Nn2GeIinKS5HAAew9dEBpuEBzsZRhuUP5cKhcPRo9OKqNL/hp5MIo9lTWu414l1Ksv5Pjx6w6oxpTQ++vChR2S/F2QGqEvj9bsw/NKJA5Zbm6uTmiDfqJUZmam1ROnymvatCm+/vprdOnSpdrF6XQ6xMbG4uOPP4ZcLodarcZrr70GpdL8B2zFHi2qHdLSijBt2l9ITS02tAUFueGP+DXw8zhpsv+eoyF4aOIUDBnSGO++286RpVbqzTfPYedO0wBjy1rT0oqwYkUKsrJK4OfniilTgtG0qbthW/lzqWiajY/n7EafHho4ufojrWQKSnRNbVLHvWjixBM4cya/0v0aNnTBrl29HVCRMUe8v+5F5v7GLF3a2ezvjtA+jhTGO4RQHWe2JzUhIQEA4OrqavRzZTQaDTIzM/HJJ59gxowZ2LNnT7WL27hxI77//nusXr0abdq0wenTpzF79mw0b94cTz31lOBj+EtdPUlJSaKeu7AwYNu2FkbjPJXKcNzn9RtQbBpS07PKejYKC+UOq9tSD0v581dQcEHw8basNSwM6N+/k9ltxucyBKF9nofrv7VKcU6/2O+/8vLyEq3ar3v3AFFqdsT76160cOEeo/AJlK1vvGJFCr7/foTFfdatuyGpNZCJ6gqzIfXBBx+0+HNlioqKMGvWrOpV9a+5c+di2rRpGD16NACgffv2uHr1KhYtWmQ2pFLtVXGcJwAUq5WQlyYaXfK/qGoI5eKysYBSWvZJT+wlqgDhc0nW8fNzx5UrBRb3cXNzwoIFvRxUkTFz76/z53MQE7OHl6fNMDfuPSurpNJ9HLkGMhHd5WSvA48ZMwbHjx+v0TFu374NuVxu1CaXy6HVas08gu41OmcFChvGI0cThcN/tsY3CV0x6NlJUKX5Go3DtDdLqw9UpFSGIzjYOCQ4slaqmZYtLQc8Dw9n/PSTeOM/hd5fAJCVVYwNGy4hKmoHVKrKx9TWNebCvZ+fa6X7OPILJhHdZTakxsbGIicnp8oHzM7ORmxsLOrXr4/mzZvXqLghQ4bgk08+wa5du6BSqZCQkIBly5YhMjKyRsel2kXnrIBT0Jdo0O4XbDn+Jpq37IDo6BCHThSpSg+Lfomq6OgQ9OkT6PBaqWaEQqCHhzPCw/0QHR2Cw4dHo3fvJiJVZ/z+8vNzM9lu7stTXWfuy+OUKcGV7sMvmETiMDtxqm/fvkhOTsbw4cPx6KOPonfv3qhXr57gQYqLi3HgwAH89NNPSEhIQFhYGPbt21fj4vLz8/Hee+9h69atuHHjBvz9/TF69GjMnDkTbm6mf5yp+qQ0JlCKYmL2YMOGSybt0dEhWLVqIM9fDUnt/OnHH5cfHy3FLxmRkVtx8GCGSXufPoFISOCX+YqEXteSkmtG773a8toT1QVmQyoAbNq0CUuWLMHJkyfh4uKC1q1bQ6FQwNvbGzqdDrm5uVCpVLhw4QLUajW6dOmCl156CSNHjnTkv4FsQGohQWqExqQGB3sZekh5/mqG5696xo3biR07rpq0R0Q0w3ffDRGhotqH7z0i6bK4mP/IkSMxcuRInD17Flu3bsXvv/+OP//8Ezdvlq252LBhQ7Ru3RrDhw/H0KFD0b59e4cUTeRoQneZYg8Lic3csoCOvoU1EZE9WHXHqfbt2zOAUp3HGfMkNXl5pYLt+fnC7UREtYndZvcTEZF9cTY6Ed3LGFKJiGoppTIcQUHGk0g5G52I7hVWXe4nIiLpUSi8sHRpZ6xbd4NjpYnonsOQSkRUizVt6s6x0kR0T+LlfiIiIiKSHIZUIiIiIpKcaoXU1NRU/PnnnygoKLB1PUREREREVQupW7duRbdu3dCpUycMHDgQJ06cAABkZ2ejV69eSEhIsEuRRERERFS3WB1Sd+3ahaeeegqNGjXCrFmzoNPdvZuqr68vgoKC8O2339qlSCIiIiKqW6wOqQsXLkT37t3x888/IyYmxmT7Aw88gNOnT9u0OCIiIiKqm6wOqefOncOoUaPMbvf398eNGzdsUhQRERER1W1Wh1RXV1fcuXPH7ParV6/Cy4sLSBMRERFRzVkdUnv06IFNmzYJbsvLy8O6devQp08fmxVGRERERHWX1SF19uzZOHv2LKKiorBjxw4AwKlTp7BmzRr069cPeXl5mDlzpt0KJSIiIqK6w+qQ2rVrV/z4449IS0vDtGnTAABz587Fq6++Crlcjh9//BGtW7e2W6FEREREVHc4V2XnBx98EMePH8fp06dx6dIlaLVaBAcHo0uXLpDJZPaqkYiIiIjqmCqFVL2OHTuiY8eOtq6FiIgsUKnyEBubiIyM2wgMrA+lMlzskoiI7Mbqy/0+Pj5o1aoVDh06JLh9/fr1aNiwoc0KIyKiu1SqPERF7cCGDZdw8GAGNmy4hKioHUhLKxK7NCIiu6jSbVHv3LmDqKgoLF++3F71EJEVVKo8xMTsQWTkVsTE7IFKlSd2SfckKZ3n2NhEpKQYP39KSh5WrEgRqSIiIvuq0uX+999/H8eOHcN///tfnDx5Ev/73//g5uZmr9qoDpKpVXDLj4WTJgNaeSCKPZXQOSvELktS9D1q5QNLYmIW4uMjoFBwrWJbkdp5zsi4LdielVXi4EqIiByjSiHV1dUVixcvRpcuXTB79mxcuHAB33zzDZo1a2av+qgOkalV8LgZBbnm356hUkBemojChvGSCqrlxwV6eblAp9Ph+vU8tGx5FUpluN0DjLketdjYRKxaNdCuz30vqzjes6CgRFLnOTCwvmC7n5+rgyshInKMak2cmjhxItq1a4ennnoK/fv3x5o1a2xdF9VBbvmxdwPqv+SaFLjlx6LIZ5VIVRkT6l3TO3HilkN62sz1qGVmCrdT5YReVzc3ueC+Yp1npTIciYlZRjUGB3thypRgUeoxR2hyF3v4iag6qhVSAaB79+7Yt28fnnzySYwePRo9e/a0ZV1UBzlpMsy0Zzq4EvMq9mIqmmYj9uVdaNI4D+nXvaBcPNjuPW3metQCAoTbqXJCvdPFxRrBfcU6zwqFF+LjIxAbm4jMzNsICCgLgCUl10SpR4jUhkhYi8GaSJqqHVIBIDAwENu3b8err76Kb775hmulUo1o5YFAqVB7gOOLMaN8L6aiaTZ2f/4ZQhU3DW09Oqnw3xWN7VqDuR41LkdUfeZ6p93c5EZhVezzrFB4mXwBSkqSTkitjUNR0tKKMH167QvWRHWB1SH1r7/+QqNGjUzaXV1dsWTJEgwfPhxZWVk2LY7qlmJPJeSliUaX/DXyYBR7KkWsylj5XszYl3cZBVQACFXcxIuPbQLwjN1qMNejxg/U6jPXOz1wYFN4eLjwPFupNg5FWbEipdYFa6K6wuqQ2rx5c4vb/+///q/GxVDdpnNWoLBh/L+z+zOhlQdIbnZ/+V7MJo2FlyPq2lEN4QvFtiPUo0bVZ653ev78ngylVVAbh6JkZd0RbJdysCaqK8yGVP2i/b179zb6uTL6/YmqQ+esEJwkJZUxY+V7MdU6fwCXTPZxrR8ELq9eu7B32jZq41AUP796gu1SDtZEdYUsNzdXJ7TBx8cHMpkMmZmZcHV1Nfxsjk6ng0wmw82bN83uQ9KVlJSEsLAwscsQJDQZIzjYS/QxYyZLZqFseILUlsyqDaT8/pM6qZ07/RfK2hL29+07henT/5bc3xcistCTmpCQAKBszGn5n4kcTaqTMcoPTyguSIZbg5aSG55A5Gi1bShK06bu7EUnkiizIfXBBx+0+DORo0h5MoZ+eELSjSSENZNObxYRWa+2BWuiusKpJg9OS0vDiRMnkJuba6NyiEzVxskYREREVDMWQ2piYiLi4uJMlpa6du0aIiMj0bFjR/zf//0fwsLCMG/ePLsWSnWXUhmO4GDjS29Sn4xBRERENWMxpH7++ef4+uuv4efnZ9T+wgsv4NChQ+jZsydeeOEFtGnTBkuWLMF3331n12KpbtLPvI6ODkGfPoGIjg7hpAYiIqJ7nMV1UhMTEzF06FCjtpSUFPz6668YOHAgfvrpJwBAaWkpBgwYgK+//hrjxo2zX7VUZ3HMGBERUd1isSf12rVrJkub7Nq1CzKZDBMmTDC0ubi44NFHH8W5c+fsUiQRERER1S2VTpzS6YyXUT127BgA00X7/fz8UFTEJcyJiIiIqOYshtTg4GAcPXrU8LNarcaBAwfQqlUrNGzY0Gjf7OxsNGrUyD5VEhEREVGdYnFM6rhx46BUKhEWFoZevXrhxx9/RHZ2NqZMmWKy76FDhxAaGmq3QomIiIio7rAYUp999lns3bsXcXFxkMlk0Ol06NOnD1544QWj/a5evYo9e/Zg7ty5di2WiIiIiOoGiyHVxcUFP/zwA06ePImUlBQ0b94c4eGma1OWlpZi9erVJuNUiYiIiIiqw2JI1evatSu6du1qdnvLli3RsmVLmxVFRERERHVbjW6LSkRERERkDwypRERERCQ5DKlEREREJDkMqUREREQkOVZNnKJ7m0qVhzffPIeCggsIDKwPpTIcCoWX2GURERFRHcaQWsepVHmIitqBlJQ8Q1tiYhbi4yMYVGsplSoPsbGJyMi4zS8dJBq+D4mopsyG1Li4uCofTCaTYebMmTUqiBwrNjbRKKACQEpK2YfLqlUDRaqKqotfOmyHIav6pP4+LP/aNmigQVycvyTqIiJjZkPqggULqnwwhtTaJyPjtmB7xeBK0qb/0N23Lw1ZWcVG2/ilwzxzQVQoZG3frsL69YPRu3cTESuuHaT85Vfotb1wYYdkAjQR3WU2pObk5DiyDhJJYGB9wfa//86BSpUnmT/aju7VqsrziT2mV+hDt6J9+9IQGbmVPYLlWOrtEwpZhYVqjBmzC4cPj5bM+RP7vWeOuS+/mZnC7Y4k5QBNRMY4JrWOUyrDsX27CoWFaqP2wkK1ZP5om+vVatPGBy1betn8g7kqlyodXZsQoQ/dirKyipGVlQFAWpddxWQprJg7n4WFagwatBn9+zcVPRBK+ZK6uS+/AQHC7Y5kLkD//fdNB1dCRJWR/BJUmZmZmDJlCkJCQuDv74/u3bvj4MGDYpd1z1AovNC2rY/gNin0egDCYaKwUI0TJ7KwYcMlREXtgEplu+EJlsJLeSpVHoYN2+bQ2oSY+9A1R+jfIhUqVR5iYvYgMnIrYmL22OXcydQquOfEYNbjb+Drhd9C0TTbaHtm5m1cv15k9vFZWcUOe20tmT37sFXvUzEoleEIDjYOysHBZV/axGYuQJ89m4NDh9IdXA0RWWK2J3XYsGFVPphMJsOWLVtqVFB5ubm5GDx4MHr06IH169fD19cXKpUKfn5+NnsOKvvwSEzMMmmXQq+HSpWHffvSLO5j60t11lyqPHQoHWPG7DLpgbZ3bULMfej6+blBo9Hh5s07JtsuX863Wz3V5YieQZlaBY+bUZBrUnB/G+D+NkCPTioMenYSVGm+AMre97dvq3HlSoHFYznqErHQ0BMA+PVX4d8LKXy5VCi8DMMmMjNvIyBAOkMRlMpwbNyYDI1GZ9Su0wFTp+7HqVPjRKqMiCoyG1K1Wi1kMlmVDqbT6SrfqQr+97//ISAgACtXrjS0tWjRwqbPQWV/tI8cSUNq6t0JN1Lo9dCHlooTgYTY8oO5skuVKlWeVQHVHrUJUSrDkZiYZRTugoPLQsKwYdsEQ+q1a+IHmYocMVbQLT8Wck2KUVuo4iZiX96FJ2c+bnjfx8Ym4sQJ0y9uFdn7tTUX3Bs3dkdJiVbwMVL4cgmUBVUpDBeqSKHwgru7HAUFpr+/GRmFkhqLT1TXmQ2p27Ztc2QdZmt46KGHMHHiRBw4cAABAQF46qmnEBMTYzZAJyUlObjKe8PSpZ2xYkUKsrJK4OfniilTglFScg1JSddEq+nNN89ZvcqAh4fGZq/9+PGNTEJ7UJAbxo9vhKSkJLz55jmrA6qtazNn0aK2gq+fp6fw/p6eMsn9riQn3zDTnm2zWlu5JcNV4K+eokk++vZtiBkzwlBSck3wPSDE3q+t0O9ASkoeLl82/3uhf5+SeZ6ewiG1tFSHwYPjsWJFFzRt6i5CZcbCwsLELoFIVJKeOHX58mV8/vnneP755/HKK6/g9OnTmDVrFgBg0qRJgo/hL3V1JeH770eIXYSRgoILVu0XHOyFuLgBNuv9CAsDtm1rYfZSpbV12aM2c8LCgP79O5m0t2t3FWfPml62bteusaR+V5KSktCyZSOcOHHLZFvLlr42q9UtpyVQfMKkXZXuiatX1QgObgGFwsvoPXD5cj4uX76FrCzjHmlnZxlefPEBhIXZb0mqqrzX9PT/BjJv9WoPjBixHWq16dW/zMw7+OyzDHz77WARKiOi8qo0cUqj0WD9+vWYNm0axo4dizNnzgAoGzu6adMmZGZm2rQ4rVaLzp07Y968eejcuTOeeOIJTJ48GatXr7bp85A0mbvsrufn54bo6BC7zGbWX6pMSIjEqlUDjY5fWV0eHs4ID/ezW21VIeUJLBU5otZiTyU08mCjtouqhlAuHmwYWqCfvPXCC7+hsLAUV67kmQRUAFCrdfjyy/M2q02Iufeaq6v5P91SmDgldb17N8HmzY/AycxpPH78umMLIiJBVvek3rp1C6NGjcIff/yBBg0aoLCwEM8//zwAwNPTE2+88QYee+wxzJ0712bF+fv7o3Xr1kZtrVq1Qmpqqs2eg6RLaKxleW3a+Igy5k2oLrkcaN++IVq39pHMBBFA2hNYKnJErTpnBQobxuNowlQ44xrSs7ygXDzYMGkqJaXyNWfLE2u8sVJ5P559dq8oNd0revduAl9fN6vGvBOROKwOqW+//TbOnz+PDRs2oGvXrggNDTVsk8vlGDZsGH755RebhtQePXrg4sWLRm0XL15Es2bNbPYcJF360DJs2DbBmdZiTRARClPjxzcSvNwuBVKdwCLEEbXqnBVYvf01bNhwyWTb9etFlc7qL8/e70FLwf3rry9g3z7TJZOkMnGqNggP98OOHVcF24lIfFZf7t+2bRsmTZqEQYMGCU5aCgkJwdWrpr/sNfH888/j+PHj+PDDD5GcnIz4+Hh89tlneO6552z6PCRdCoUXEhKGSu6SdcXhAFKYZEHWMze0oHFj619HR70HzQ09Wby4j+R+L2qbBQt6wd/f1agtKMgDCxb0EqkiIirP6p7U3NxcBAcHm92u0+lQUlJik6L0unXrhnXr1uGdd97BBx98gKCgIPz3v/9lSK1jatMla6odzL2nYmMTBdcMrqhJk/qijzfW/xtmzdqLwkI5fy+qQaHwwsqVXbFu3Q3+bSGSIKtDavPmzXHu3Dmz2w8dOmQ0BMBWBg8ejMGDOcuyrqtNl6ypdhB6TwmPN5YZLfweFOSBbdsiJRFkFAovvPtuO0mt1FDbNG3qzr8tRBJl9eX+6OhofPXVVzh06JChTX/Zf+XKldi6dSsef/xx21dIROQg+t7J6OgQ9OkTiOjoEGzZ8ojRz1IJqERE9zqre1KnT5+OxMREDB8+HKGhoZDJZJg9ezZu3ryJa9euYejQoZg8ebI9ayUisjuhHtbeve23FioREQmzOqS6uLhg/fr12LBhA+Lj4yGTyaBWq9G5c2eMGjUKY8aMqfJtVImIiIiIhFT5jlPR0dGIjo62Ry1ERERERACsGJP6008/YdeuXRb32bVrFzZu3GizooiIiIiobrMYUrdu3YqYmBjI5XKLB3F2dsZzzz2Hn3/+2abFEREREVHdZDGkrlu3Dj179sSgQYMsHuShhx5C7969sXbtWpsWR0RERER1k8WQeuLECavXKP2///s/JCYm2qQoIiIiIqrbLIbU3Nxc+Pr6WnUgX19f5OTk2KQoIiIiIqrbLIbU++67DxkZGVYdKDMzE/fdd59NiiIiIiKius1iSO3WrRs2b95s1YHi4+PRrVs3mxRFRERERHWbxZA6YcIEnDlzBrNnz4ZWqxXcR6fTYc6cOTh79iwmTpxolyKJiIiIqG6xuJh/REQExo8fj5UrV2Lfvn149NFH0a5dOzRo0AAFBQU4d+4cfvzxR1y4cAFPPvkkhgwZ4qi6iYiIiOgeVukdp5YuXYpWrVrhk08+wXvvvWd061OdTgdvb2+88847ePHFF+1aKBERERHVHVbdFvWll17CpEmTcPToUVy4cAH5+fnw9PRE69at0aNHD7i5udm7TiIiIiKqQ6wKqQDg5uaG/v37o3///nYsh4hIelSqPMTGJiIj4zYCA+tDqQyHQuEldllERPc0q0MqEVFdpFLlISpqB1JS8gxtiYlZiI+PYFAlIrIji7P7iejeoVLlISZmDyIjtyImZg9UqrzKH1SH6c/XoEGbjQIqAKSklPWsSgVfWyK6F7EnlagaKl7+HT++EcLCxK7KPPYGVo3Q+apo3740qFR5op+/tLQiTJ/O17a60tKKsHDhHg7lIJIghlSSjNow7k+lysOcOUfw669puHNHA0XTbEwevgt+twugTW0PecDb0DkrxC7TRGxsotnewFWrBopUlXQJna+KsrKKERW1Q/QwuGJFiuBrO2fOEXh4uEj690lsKlUepk37C6mpxYY2Bnwi6WBItSOZWgW3/Fg4aTKglQei2FMpyQAjBbWhp69ijYqm2dj9+WcIVdz8d48kaG7+hcKG8ZJ7nZOThQNXZUGsrsrIuG3VflII+llZdwTb9+xJQ3GxxvCz1H6fpCA2NtEooALSeE2JqAzHpNqJTK2Cx80ouBZvgHPpQbgWb4DHzSjI1CqxS5MkSz19UlGxxtiXd5ULqGXkmhS45cc6urRKZWUVCbZfvy7c7kgqVR7efPOcpMZTBgbWt3rfy5fz7ViJsPJjUNPTiwX3KR9QAfF/n6Q4btbcl5HMTOu+pBCRfZntSY2Li6vywWQyGWbOnFmjgu4VbvmxkGtSjNr0AabIZ5VIVUmXuQ8LqYz7A0xrbNJY+EPWSZPpiHIqpR+acPz4deTkCPe2+ftbH8bsQWo96PohJykpeXByAszcDdrItWuODTTWjJd1c5ObhFTAMeFLaNgOAEm9znrmvowEBIj7e0FEZcyG1AULFlT5YAypdzlpMgTbS26nAj4OLqYWMPdhIZVxf4BpjenXhevRygMcUY5FKlUehg7ditTUQov7NWpUz0EVCZPSWFlrwp+Qxo3d7VTRXeWD35Ur+bhypUBwPzc3OQYObAqdTocdO66abLd3+DL3paNtW2/RXmdLY92VynAcOZJmdMk/ONjLEKyJSFxmQ2pOTo4j67jnaOWBQKlp++59GrR8UBo9g1LytrIxHu+/AF4e2Ui/7gXl4sFQpfkCkM4YMaUyHImJWYYPW+XiwejRWYXQ5ncv+WvkwSj2VIpVokHZWDvLARUATp++KWpPtZQut1ozWUqISpWPmJg9dpuYVJXwXFysgYeHC5TKcJw/b/wYR4Qvc186CgpKBPe39+tcWU+9QuGFpUs7Y926G8jMvI2AAE4wI5ISjkm1k2JPJTKz/Y3aLqoa4pX3B0pqnKUUyNQqtHJ/ElEDj2Fg90t4YthJ7P78MyiaZhv2Kf9hJtbYNoXCC/HxEXjkkeZwc5NDleaLQc9MwjcJXXHoZBhyNFGSmTRl7cSf1NRCUd+PUrrcau05qygrqxgbNlxCVNQOu7wXqxqeMzNvG96r0dEh6NMnENHRIQ65GlHVc2jv19mase5Nm7pj1aqBSEiIxKpVAxlQiSSEs/vtROeswIsfzMKI3l+jiV8e0rPu9g4256B8I0Ljd0MVNxH78i48OfNxAHc/zNJVZ5B8cAamDL3b4xoV5bixbQqFFzw8XAzj/VRpvoYao6NDsGqV+AEVqNrEHzEniVTsnQbEu9xalXMmxF49/tUNfgqFl8OvPpg7h+Hhfjh//pbDX2cp9dQTUdVVKaSeP38eK1aswJ9//olbt25BW2FWgUwmw59//mnL+mo1mWsLQ4Apj4PyjZkbv9vEr+wDTf9hJlOr4JM/GlEDrxn26dFJhUHPTnLocIDa8MFXNtYu06pL/mK+H/U9frNm7UVhoVzUy61Cgbmq7PEeMBf8mjSpj5s37xhNkBJ7PKW5Lx0LFvQCUNaz6cjL6lLqqSeiqrM6pP7++++IiopCgwYN0K1bN/z111/o27cv7ty5g2PHjqFNmzbo0qWLHUutfaTUSyRl5sbvquGP6OgQw4eZW86r8PK9ZrSPvsf1s4QODqq2dnzwKRRe2LYt0jC7HwDatfPGpUv5RsFVCu9HhcIL777bDmEi37JLH5j1QUqlMj9ByRx7vAfM/R2Jj48AAEkEfL2K57BiTY7u2eXfYKLaTZabm6uzZsdhw4YhPT0dv/76KzQaDUJDQxEfH49+/frh999/x5gxY/DFF19g4EAugAzcXci/5HYqTp52xpLvRwIuLUT/EDEnKSlJtJCgX1O2/CV/jTzYZHynx41IOJceNHn8nqMhWLH9A4d9AApNxggKcsO2bSMk+dqWp5/pLLVJImK+/8yJjNyKgweFe/nd3Jzg7e1m1HOqD472mjxl7nWT4rmTksre8zx/RNJldU/qyZMn8frrr8Pb29sw819/ub979+54+umn8d577zGkwjh0uToBfToDvbql/hu6xA8EUqNzVqCwYfy/d+fKhFYeIHh3LnM9rnm3fR3aMyLUWzR+fCNJhL3KiDFOsbayNEa1uFiLrl190aBBoEMCP1+36uO5I6q9rA6pMpkM9913HwCgfv2yP943b95deic0NBSrV6+2cXm1Exfyrzqds6LSc1PsqYS8NNHo3GZm+6P1gx+jiYMDYsUPvqSkJIc+P9lfZWNUCwrU+O67IQ6uioio7rB6CarmzZsjOTkZAFCvXj0oFArs3bvXsP3w4cNo2LCh7SushcxNBJLKnYhqK32Pa4lbNNQufVDiFo36bX5GE4XjxqNS3aHvMW/evIHgdimNQSYiuhdZHVIHDBiAzZs3Q6crG8L69NNPY926dRg+fDiGDRuGH374AdHR0XYrtDbRygPNtIt/J6LaTt/jWtgoAUU+qySxJinduxQKLyQkDEVwsHFPPSffEBHZn9WX+1977TU8+uijUKvVcHFxwSuvvAKdTodNmzZBLpdj9uzZmDFjhj1rrTWELktL5U5ERFQ1lc1YJyIi+7B6dj9VjX52v6WJQFLCGa41w/NXMzx/1cdzVzM8f0TSxTtO2Yk1E4GIiIiISJjZkBoXFweZTIbXXnsNTk5OiIuLq/RgMpkMM2fOtGmBRERERFT3mL3c7+PjA5lMhszMTLi6usLHx6fyg8lkRstSUe3BS141w/NXMzx/1cdzVzM8f0TSZbYnVb9gv7mfiYiIiIjsxeolqIiIiIiIHIUhlYiIiIgkx+zl/mHDhlX5YDKZDFu2bKlRQUREREREZkOqVquFTCar0sH0d6MiIiIiIqoJsyF127ZtjqyDiIiIiMiAY1KJiIiISHKqFFI1Gg3Wr1+PadOmYezYsThz5gwAIDc3F5s2bUJmZqZdiiQiIiKiusXqkHrr1i08/PDDmDx5MjZv3oxffvkF2dnZAABPT0+88cYb+Oyzz+xWKJFUqVR5ePPNc4iM3IqYmD1QqfLELomIiKjWszqkvv322zh//jw2bNiAP//802iSlFwux7Bhw/DLL7/YpUgiqVKp8hAVtQM7d17HwYMZ2LDhEqKidkgiqKpUeYiJ2cPwXA08d0RE4jM7caqibdu2YdKkSRg0aJDgrU9DQkLwww8/2LQ4IqlRqfIQG5uIjIzbCAysj8LCUqSkGAeYlJSyfVatGihSlXfDc/naEhOzEB8fAYXCS7S6agOeOyIiabA6pObm5iI4ONjsdp1Oh5KSEpsURSRFQuGlXj254L6ZmbcdVRaA2hOepUymVsEtPxZOqX/jnakuUC4eDFWaL4CyczdnzhF4eLgYzrFSGc7QSkRkR1aH1ObNm+PcuXNmtx86dAihoaE2KYqovIoBTKxwEBubaBL87tzRCO4bEFDfESUBkHZ4Nqfiazp+fCOEhYlXj0ytgsfNKMg1KejQEujQEujRSYVBz04yBNU9e9JQXHz39ZZy76pUfmeIiGrC6jGp0dHR+Oqrr3Do0CFDm36x/5UrV2Lr1q14/PHHbV9hOR999BG8vb3x+uuv2/V57kUytQruOTHwuBEJ95wYOBUfMvrZVZYmdomC9AHs2OFjmDz8I0wZ+jqSDz6KdNUZh9eSkWFdwHNzk6OgoMRh4xilGp7N0b+mGzZcMozjnTbtL1HHfbrlx0KuSTFqC1XcROzLuww/lw+oQFnv6qBBmyU3ZlXo/EplnLRUlB9z/Oab53huiCTK6p7U6dOnIzExEcOHD0doaChkMhlmz56Nmzdv4tq1axg6dCgmT55st0KPHz+OtWvXon379nZ7jntV+V4iAEAp4FK8CTKoDT+3cj+CEvU26JwV4hVajr4naN++NNR3TcPuzz9DqEI/FvoSMrNHQ6b+2aH1BgbWh6JpNmJf3oUmjfOQft3L6JKwkxOg1ZaFmR07ruL8+R0O6WmzNjw7O8swZEhzxMTsMfSwTZjQBl9+ed6hPW5CoTo1tRjDhm1DQsJQUXr88nJUaORu2t7Ez3J4ycoqxoYNl0TrVT10KB3PPXcEhYWH4O1dD8uX98OXX57nUA8LVKo8DB26FamphYa2M2e2Ytu2SPY2E0mM1SHVxcUF69evx4YNGxAfHw+ZTAa1Wo3OnTtj1KhRGDNmTJVvo2qtW7duISYmBkuWLMHChQvt8hz3MqFeIkNA1e/jlAqn/FgU+axyZGmCKl6+/nrhrnIBtUyA7zWUOLjet5WN4X7jc7RokmVoK39JWKs13t9RwSAw0LreUbVah5deOoDCwruv/aZNyVCr767U4YiwZS5UX7lSgKgoxwT78g4dSkfOuVKMjzTdlp5lXR1ihMBDh9IxYsR2w+uXl1eKESO2o3Vrb8H9pTLUAxB3OMLs2YeNAioApKYWYvbsw/juuyEOqYGIrGN1SNWLjo5GdHS0PWox65VXXsGIESPQr18/htRqcNJkWLmf42/GYJisosmAVh6IYk8lYmMvGfUENWks3JtVcjsVMTP3OOyDLsRrMVxds4za9JeEn5wpPNTFEcFAqQxHYmKWyZhUoUv+5QMqAKOACjgmbFkK1WKEvalT90OmGYzuHVVGX4YuqhpCuXiw1cdxdAicOnW/yeunVuuQkpIvuL8UhnoA4q+ekJiYVaV2IhJPlUOqo61duxbJyclYuXKlVfsnJSXZuaLaJ7heA/i6VL7frdseSHHg+XOVpaGV+zS4OqWWNZQC2ttHUJQ3FYCrYb/068IfXD/vLcWGDZcMPx85koalSzujaVOB67Y20MotGa4CvzFN/PLg7u6EoiKtyTYPD41D3pOLFrXFihUpyMoqgZ+fK27f1uC337Krdazk5Gy71jx+fCMcOZKG1NRiUZ6/ops3i1BQ4ItBz04qG8rhl4f0LOOhHNZw1Gutd/NmkWC7TKZFUJCb0fkNCnLD+PGNJPH38c03zwkOR5g1ay/efbed3Z9foxEer63ROPb1s0aYmLMJiSSgSiF13759WLt2LS5fvoycnByjBf2BsolUf/75p82KS0pKwjvvvIMdO3bA1dW18geg9v1SC/Uk2nqcpUwdB83NC0aX/HVwNrrkX6wNgkuTOIQ5cIyne85CuBanGrW5OaVi5sSd2LpruKFNuXgwenQy7uVKTm2EGfMHGT02NbUY69bdsFsvnFtOS6D4hEm7i3sTLFrUEXFxKUYfvsHBXnjxxQewcKH9x3yGhQH9+3cy/CzUW+Xh4WzSkyqkZUtfu/4ehYUB27a1wLBh23DlSoHDn7+ihg0TUVBQAFWar9ke8coEB3shLm6AQ4cpeHkdQ0GBae+tr299JCQMRWxsIjIzbyMgQJzZ/eYu6RcUXBDcv7BQbvfXXaXKg5ubC4BSk209egTWus8Ponud1SF1+fLleOONN9CoUSOEh4ejbdu29qwLAHDs2DFkZ2ejZ8+ehjaNRoPDhw9jzZo1SE9PR7169exeh70ITWiSlyaisGG8TYOqzlmBwobx/4bhTGjlAbjjPgH1ir40/PxP9ngoHDxpytwwhK4d1QgO9jIELFWaaS/Xu8sjoErzMXmsPS+5FnsqIS9NNAr7GnkwOg9aCveUEsTHtzEKBhMmtMG0aQdEuaypUHghPj7CpJ7Ro3eazFIvLzjYC0pluF1r09eXkDDUJEg76vnLW768n9HYTms5OQHduvkZanZkCFSp8qDRmPbcy+Vl/x6FwkuyN5MwN9zD3sMR9DWlp5v+jQgK8sD8+T0FHkVEYpLl5uZa9Ze5Q4cOCA4Oxk8//WR1r2ZN5ebmIj093ajthRdeQEhICGbMmIG2bdvabbKWI7jnxMC1eINJe4lbtMMnMCUlJTm8F8HSv/983keIjU3E5cv5OHfuplU9gAAQHR1i1w/nuz3fZeFe3/MtdP5iYvYYDUdwVI2WjBu3Ezt2XDVp9/NzQ//+TUUJW7GxiUhOzkbLlr6ired56FA6pk7dj/T0QqvDakREM9Em2ph7b9WrJ8OxY2NEn6Vu6b2vVIYLfjmx95c3czUFBtbDzp1Rop8zIjJldU9qdnY2Xn31VYcFVADw9vaGt7e3UVv9+vXh4+ODdu3sP3bJ3sz1JIoxgUkM5nomiz2VUPjc7QlSqfLMXhouzxG9cDpnhdVfIMzNYhdzlvWCBb1w/rzjA4I5+h4/Mb4klde7dxOcOjUOKlUeevX6qdIvRcHBXliwoJeDqjNl7r11545OEktNWXrvC/XyO+LLibmamjRxZ0AlkiirQ2qXLl1w5coVe9ZS52jlgUJDo6CVBzi+GBEIDUMQGpOrUHiheXNPwZDq5+eGNm18RBt3Z4lYlzUtESsg1BYKhRfWrx+MMWN2GQXVoCAPdOrki/z8UkmcM0srJEhhqanK3vtiDEcwV5Ofn+M6XoioaqwOqe+99x7GjRuHAQMGoG/fvvasyaJt27aJ9ty2Zqknsa6wtmfS3AdM//5NRe81MkdoaSgxxlxWJPZ4Ranr3bsJDh8eLekgr1SGY/t2lWCPrxSWmpLie99cTVOmBItWExFZZnZMqtBaqJcvX8alS5cQEhKCZs2aQS43vj+4TCbD+vXr7VPpPcrcGEdHE/tya2WEJmKIeZm6InPnTz/mUqphRyqk/v6TokOH0k16fKX0OyHF975QTSUl1/jeI5IosyG1Y8eO1ZqUdOrUqRoXRY5XG0KCFD/09GrD+ZMynr/qUanK1hctLJRL7neituB7j0i6zF7uP336tCPrIKoUL1MTGVMovPDuu+0YsojonuRk7Y6HDh3CjRs3zG7Pzs7GoUOHbFIUEREREdVtVofUYcOGYe/evWa379+/H8OGDbNJUURERERUt1kdUiveArWikpISODlZfTgiIiIiIrMsLkGVl5eHW7duGX6+efMmrl41vVtNbm4ufvrpJwQGBtq+QiIiIiKqcyyG1E8//RQLFy4EULa81Jw5czBnzhzBfXU6Hd58803bV0hEREREdY7FkNq/f3+4ublBp9PhnXfewahRo9CxY0ejfWQyGerXr4+uXbsiPFzcRcqJiIiI6N5gMaT26NEDPXr0AADcuXMHw4YNQ/v27R1SGBERERHVXVbfFnX27Nn2rIOIiIiIyMBsSP3uu+8AAI899hhkMpnh58qMGzfONpURERERUZ1lNqQ+//zzkMlkGD16NFxdXfH8889XejCZTMaQSkREREQ1Zjak/vXXXwAAV1dXo5+JiIiIiOzNbEht3ry5xZ+JiIiIiOzF6olT5Z05c8awqH+zZs3Qvn17yGQymxZG9iVTq+CWHwsnTQa08kC4ysYDCBO7LCIiIiIAVQypP/30E+bNm4f09HSj9iZNmmDevHmIjo62aXFkHzK1Ch43oyDXpJQ1lAKt3I+gRL0NAIzCa7GnEjpnhai1SqkeqhxfMyIisgWrQ+q6deswbdo0hIWF4e2330ZoaCh0Oh0uXbqEr776CpMnT0ZJSQnGjx9vz3rJBtzyY+8GVH2bUyqccl+GXKsyCq/y0kQUNowXJWQIhWkx66HK8TUjIiJbkeXm5uqs2fH++++Hj48Ptm7dCjc3N6NtxcXFeOSRR3Dr1i2cOHHCLoWSbcjUKjS4MQhOuiyTbTo4QQatSXuJWzSKfFY5ojwj7jkxcC3eYNJ+4K8+uK/tOigUXg6vyZykpCSEhXG4hLnXrLL3EM9f9fHc1QzPH5F0OVm7Y1paGqKjo00CKgC4ublh7NixJsMAyJhMrYJ7Tgw8bkTCPScGMrXKoc/vVHwInlm9BAMqAMGACgBOmkx7lmVCpcpDTMwenDpxWnB7aVE6oqJ2QKXKc2hdgPivYUX6cxUZuRUxMXtEOSflOWkyzLQ79j1ERES1n9WX+9u0aYOMDOEPIABIT09H69atbVLUvUjsy6AytQoeuWMgQ2GVH6uVB9ihImEqVR6ionZAW5KChpOuCe6TnuWFlJQ8DBq0Gf37N4VSGe6QXlVLr2FaWhEWLtyDlJQ8XL9eBD8/d7Rs6WXX2vTnKiXlbjBNTMxCfHyEaL3MWnkgUCrU7rj3EIlPpcpDbGwiMjJuIzCwvsN+R4no3mL15f7ffvsNTz/9ND7++GOMHDnSaNtPP/2E1157DV999RX69Oljl0Jru+peBrX381ekgzNkUBt+1siDHTqeMCZmD44dPobdn3+GUMVNk+15Ba54ZPIzOPRHiKEtONjLIcHM3DnccagHRr8YjaIi057ooCAPdOrki7y8Upt/WMfE7MGGDZdM2qOjQ7Bq1UCrjmHrMGES5FH5e0ilysOsWXtRUCCXbKA5dCgdU6fuR27uHXh718Py5f3Qu3cTscuS5LkT+vLkqN/R6uDlfiLpsjqkRkdHIyUlBcnJyfDz80NwcDBkMhmSk5ORlZWFkJAQtGjRwvjgMhnWr19vj7prhfKznJ3U5+CkMw1daucHUOj3i91r8bgRCefSg5Xup5Z1gLZeWzhpMqGVBzh8ZnZk5FZMHv4Rnhh20uw+F1UNMejZSVCl+RraqhLMqkueFoEGTkdM2vccDcFDE6dYdQxbflhHRm7FwYOmVzf69AlEQkKkxceqVHmYM+cIfv01DXfuaGxa3933feXvISkFmvKB3dkZuHDhFm7duoPiYg20Fb5/ODvLsHnzIw4Jqua+SEjp3JVniy9PjsSQSiRdVl/uP3/+PGQyGYKCggDAMP60Xr16CAoKwp07d3DhwgWjx9TltVOdig+hQU7ll9dlWuFL2rZm7jJsRTJZnqhLBgUG1keTxpbHVYYqbiL25V14cubjhrbz53PsXRpOnnZGn86m7elZ1geClJSywGGLD+vAwPqC7QEBwu16QuHGlvXpnBVWXx2IjU00qcOW58haKlUehg7ditRU64bDqNU6TJ26H6dO2fc20JaGdEjl3FWUkXFbsD0zU7jdkcoHfk9PZ8hkMly7dgstW16VRC80ERmzOqSePi08iYVMlQXU4ZBBU+m+OlljB1QEFHsqIS9NNLoMqwNQ8WuEXHsFHjejRFkySKXKQ0FBCa5l31fpvk38jD+c//47BypVnl0/ZP733UgEep81GoZwUdUQysWDq3QcW31YK5XhSEzMMulJUyrDLT5OKNzYoz5rSCXQzJlzxOqAqnfr1h07VXOXpSAqlXNXUXW/PNmbpS9nJ07cEn08NxGZsnp2P1nn7gSlygMqAGhdgu1cURmdswKFDeNRUu8R6OAKwDSg6sk1KXDLj3VIXXr6D5AdO65izscP43ax5e9PFXsv1WodYmMT7VkiZK4tMOjZSfgmoSv2HA3BNwldTYYdWMNWH9YKRdml3ejoEPTpE4jo6BCrPmTNhRtb11cZlSoPV67ki1qD3vHj16v8mPr1XexQiTFLQVSqYVCpDEdwsPF7sPyXJ7FWpKjsy5k+/BORdFhMAqtXr8bAgQPRsmVLAIBWq8U///wDhUIBd3d3o31PnjyJ7777DgsXLrRftbWA263ZcNJZ1yOjkQej2FNp54ru0jkrAJ0OMpRUuq+jlwwq/wGiSvPFroOtMHLQOcF98wpdBXsv7d2DpFSGo1cvldEwg/I8PJwREuKF3NwSNG7sDj8/N5w+fdOoh86ans6qUCi8qnxp11y4AWxfnzn6LyVXrhSIVkNNabVau/feWwqi1e1Jtzf9l6fY2ERkZt421GpuHK2jejAr+3IGiN8LTUTGLPakzpw502hx/tzcXPTq1QvHjh0z2TcpKQmrV6+2fYW1iEytgkvJ3kr306IeSlwjRLmk7lxqXU+B1snTzpUYq/gBMn3BcLO9qWcu+Av2Xtq7B0mh8EKbNj6C2xo2dMHhw6Px22+jcerUOOzeHYXvvhuCbdsiq9zTaW9CPV1ubnJERDRzWH3merWcnWVYurSPw89ReLhflR9z7Vqx3XveLPVK6sPgkCGNJfX+Au5+eUpIiMSqVQMNNVkavmBvlr6c6YndC01Exiz2pOp0phP/hdqojFt+LGQornQ/J9yBXHPeARXVgINf54ofIJZ6U5PTGpm0OaoHqWVLL5w4YXozhP/8x0cwHFSnp9PeLPV0OYq5Xi21Wocvvzzv8OWdFizohdOnrZ84pWfvnrfKXiuFwgvvvtuu1sxOF3McrVDPc3lS6IUmImNWT5yiypm7244Q/bhPR99uVO36AFzvbK90PyeN8F2p7EXoA+Tjbx7Hw/1WwsPlqqGt/EQlDw9ntGvXEC1aeDosZJm7xDplimPGFtuK2OHZUq+WGJdcFQovbNsWaejpu369CAUFpbh50/LkKEf0vIn9WtmSmONoKwb+Bg30s/vz0LKlL2f3E0kQQ6oNmb3bDuRwEphIJcatIou95kOefQpybarF/WS6qk8kqQlzPUaaJsNQ8u+am/nFvlj002A0b+mJ//QSZ+Fyc3WWlDhmKbF7hVIZju3bVSgsVJtsE+uSa8UwqFLloXv3H1FcLDwJkj1vVSf2OFqhwM91UomkiyHVhoSWedI4BcFJewMQCKli3CpS56xAoe82w2LrTuqzgjcZ0Dn5O7w2oQ8QHbwMvc1OAN7/wOFlmRD+oGNIrQqFwgvr1w/GmDG7jIKqlIKfQuGFAQOaYMeOqybbmjdvIJnxn7WJFIaaEFHtUWlITUxMhLNz2W75+fmQyWQ4dOgQbt40DjbHjx+3T4W1iH6Zp/J324G2APKSHSb7amUeDp3ZX175xdbN3epT69zCwVVRXdO7dxMcPjwasbGJSE7OluQl1wULeuH8eend1ak2u5eGLxCRfVm8LaqPj/BMZrMHk8lMwmtdZ+52pI66HWplqnOvdTLFS4Y1I+Xzp79LkVR7/qR87moDnj8i6bLYk5qQkOCoOu5ZZsepSqSnUt/7W5o+C/fVL6z0XutEdQ17/oiIxGExpD744IOOquOeJThO1cGL+FdG56xAyp13EdacvQlEREQkDZw4ZWdC41TZU0lERERkGUOqA5SfqERERERElbN4W1QiIiIiIjEwpBIRERGR5DCkEhEREZHkMKQSERERkeRUKaTm5eXhww8/xPDhw9GrVy8kJiYCAG7evInFixfj0qVLdimSiIiIiOoWq2f3p6en45FHHkFaWhpCQkLwzz//oLCwEADQsGFDfPXVV0hPT0dcXJzdiiUiIiKiusHqkPrWW28hLy8P+/fvh7+/P0JDQ422Dx06FD///LPNCyQiIiKiusfqy/27d+/G5MmT0a5dO8hkMpPtLVq0QHp6uk2Lq+1kahXcc2LgcSMS7jkxkKlVYpdEREREVCtY3ZN6+/Zt+Pv7W9yu1WptUtS9QKZWweNm1N3boZYC8tJEFDaMl8TdpmRq1b93wcqAVh4IV9l4ALwtKhEREUmD1SE1JCQEJ06cwIQJEwS37969G+3atbNVXbWaTK2CR/YwyLVXjNrlmhS43XoZcnUyZNpc6Jy8cfu+5dC69XZ8fRUCdCv3IyhRb5NEgBZSMVTfcZ+AekVfGn7mrWaJiIjuLVaH1KeffhpvvPEGevfujUGDBgEAZDIZCgsLsWDBAvz2229Yvny53QqtDWRqFdzy5sDlzq+Q4Y7gPi4l+2AYLKHNQ4OcESjw2Wz3oGoIeeoUOKnPwQm3jba7OaXCKT9WkrdvFQrVLsUb7p5HifVSExERUc1ZHVInTZqEv//+G1OnToWnpycA4JlnnkFubi40Gg0mT56MsWPH2q1QKanYq1fsqQQA4yBl7rEmP6vhkRMNrUs3u/UImoQ8M5yLN8KpeAK0br0F/42ODIDln19WeglyZBhvr7C/XJMCN4mGbCIiIqo6q0MqACxatAiPPfYYNm3ahOTkZGi1WgQHB2PUqFHo2bOnvWqUFHNjTTXObSsNgeY44TacSg/apUfQ3NAD4To0aJAzFLc9FsDt9lLIdallG0oB+Z0jKGxk/+EAd3ujf4EMpVV6rJMm005VERERkaNVKaQCQPfu3dG9e3d71FIruOXHmoRRuSYFMu0tmxzflj2ChkBtRUA1PAaAe+Fsk2Uf5LpUuN2ajSLf72pcl+DzqlVwy3kJLuoDkKF6E/BkGhVkapVol/xVqjzExiYiI+M2vLxcoNPpkJ+vRmBgfSiV4VAovESrSVdyGa8//R26tkmB3EkGtUs4iu9bwOERVVT+NRbzdSUiqguqHFLrOidNhvAGXZ7tnkN9uUaP118qd76zD066rKo/v5l259Lfa1SXOTK1Ch5ZD0OOazU6jlx7BR43o2w+NrV80Htp3CZ07aiGa/0goyEQaWlFmD59B1JShN8HiYlZiI+PcEig0debnJyH8+dz0Mj7Gg5+8ymCAv6tTQe4luyA/MZph/SO3ytUqjxERRm/xo58XYmI6hqzIXXYsGFVPphMJsOWLVtqVFB5H3/8MRISEnDx4kW4uroiPDwc8+bNE3UVAa08EEJXoWVQ2+w5ZNrqhzVrx59W69i6fJsfEwDc8ubUOKDq2Xpsqj6YaEtSsPvzzxCquFm2odh4aMaKFSlmAyoApKSUBcdVqwbapK7K6i1fy9cLttwNqOXIdakcx2sllSoPw4Ztw5UrBUbtjnpdiYjqIrMhVavVCi7ab4lOp6txQeUdPHgQzz77LLp16wadTof3338fUVFR+P333+Hj42PT57JWsacS8tJEoxCogxwyaGz2HDpZ42o/Vmg4gq3oTKYr2YZzyXGbHs+WY1NjYxORkpKHrxfuuhtQ/1U+EDvrUvH1wh/RpHEe0q97Qbl4MFRpvkb7Z2Yar6hgD/p6y+vZxfxwD47jNVXxkv6ECW0wbdoBk4Cq54jXlYioLjIbUrdt2+bIOgRt3LjR6OeVK1eiefPmOHr0KCIiIkSpSeesQGHD+LKZ56UpkGv+hgyFNn0OrbxBtR9rdjiCDcigtemYT/2wBJku2ybH09PKA2x2rIyMsgDSpLFwL6mTJhMytQor31iMJn7XDe3DB57FI5OewaE/QgxtAQH1bVaXOfp6jVj47mjLc3UvUKny8MKkrzB59E+GLxyvvfwIUlK8zT7GEa8rEVFdZPVtUaWgoKAAWq0W3t7eotahc1agyGcVtC7BNg+oACAvuVDtx2rlgTasxJgMajTI6gGn4kM1P9a/wxJcizdUe6KUEI0syLAkmC0EBpYFkPTrwmMOtfIAuOXHGgVUAPDyKMH2lWugaFoWwD08nKFUhtusLnM8PU2/dx75q7ngvsV3XHEp72V7l2SRSpWHmJg9mDLlJGJi9kClst3Y7upYuXQbvnj7Yzwx7CQGdr+EJ4adxJalyw2vY0XBwV4OeV2JiOoiWW5urlXX6K9evWr5QDIZ3Nzc4OvrW+VhAtaaMGECLl26hH379kEulwvuk5SUZJfnFtLKbQq8nE/Y/LhqbQP8eXtvtR7rKktDK/dpcHNKtXFVd2l0bjh7+3uU6JpW6/GusjS0cpsKN7nte33vaBrjjq4ZSnV+SCuZUu0a9dLSijBt2l+Q69KMx6QCKNYG4Z+ipWhR712z74NvErpi0rwnsGhRR9x/v32HqKSlFWHKlD+RmWl8IwlF02zs+/JTtAi6GwDzC50RMek5qK63x9KlndG0qbtdaxOiP7epqcWGtqAgN9HqAYCsv15ARO9jJu2bdrfDqBcnGrUFBtbD8uVdRKuV7n1hYbxVNdVtVodUHx8fq8Knm5sbevfujZkzZ+KBBx6ocYF6//3vf7Fx40bs3LkTLVq0sNlxa8I9JwauxRtsflyNUxMU+J+r9uMNs/uLf4YTbLM0VkUlbtHVmnBjz4ldFWnkwTaZ6a8fo4jSy3jxMdPZ/ZbeB6eTO0AXtN0hs79jYvZgw4ZLgtsUTbMR+/IuNPHLQ3qW8ZjZ6OgQUSb+mKtXrHoA4OqhB9Gh5RmT9tvFzmgX+ZrhnAUHe0lmVn9SUhLDTA3w/BFJl9VLUC1ZsgSfffYZrl69ikcffRShoaHQ6XS4dOkSfvzxRygUCjz++OO4dOkS1q9fj8jISMTHx9tkkf85c+Zg48aNSEhIkExABYQnUdmCxqlmfzD1wxHsFaKB6k+4sefEropsNdNfofAqF5qegQZAUbntxZ5KyIu2Qi4rMnls63ZtUeTjmCAjOB71X6o0Xzw583HBbWJN/DFXr5gTkZoqQgGYhtT6bmp8/dEhvLFsMgICuD4qEZEjWB1Sb968iaKiIvzxxx8mM+tnz56NwYMH486dO4iLi8Prr7+Ofv36YcGCBdi8eXONCpw1axY2btyIrVu3olWrVjU6lq3pJ1FZe0cnaznJbDNG014hGqj+hBt7TuwSfj77z17XOSvwT9EitPZ4FU66u2OUNfJgm46PrYx+/GxFHh7OKCw0v0SaWBN/zNUr5kQkecDb0F7fASfZHZNtPcOBhIRIEaoiIqqbrJ44tWrVKjz11FOCSz/5+vriqaeewqpVZT1WjRo1whNPPIGTJ0/WqLjXXnsN3377LVavXg1vb29cu3YN165dQ0GB8FIwYtA5K6CTC09MqS5bzbjWh2iNk23r0zhVf3KSvSZ2mRuz4qjZ64Xa+1HQ6DBK3KKhdumDErdom99UoDJKZTiCg41794KDvbB+/WBER4cgPNwPHh7OJtvFmvhjrl4xJyLpnBVQ1xMeasCVEIiIHMvqntSsrCyo1eZ7Y9RqNa5fvzvDuUmTJhb3t8bq1asBACNGjDBqnzVrFubMmVOjY9uSuQX+q8PWvW86ZwUKfRNsMg5UB6DUpT+KvRdXO3wJrzPrVKMZ/lq44bbXMrgXGg8lcHRPpn6YhVgUirJxkrGxicjMvG10Wbp37yYA7o6vrbhd7HqTk7PRsqWvJC6jF9+3APKb50V9LxERURUmTj300EO4du0adu3ahaZNjWdMp6amYsiQIQgICMDu3bsBAEqlElu3bsWff/5p86KlxlaTgTROzVHom2CX3reyW48OgRyVX27XAYLL9pe4RqDI9zub1OKWHwsnTSa08gA43/kVTrqblT+wHC2coHW+H1rnFoYJTBWPW/62pfbGyRc1I7XzJ+Z7qaqkdu5qG54/Iumyuic1NjYWo0ePRnh4OCIiItCyZUsAQHJyMnbs2AGdTme43F9cXIz169dj8ODB9qlaYiou8C/TpEGGbDihxOpj2GomusUa/XbC48ZQyHWWl6cqde4Hue6KaU/SfQtsVkv5HkfPzKp/QKjrDUFRw28tHpeouvheIiISn9UhtWfPnti1axfef/997Ny5E0VFZTOZ3d3dMWDAAMyZMwcdO3YEULYM1T///GOfiiWq4oeaUO+qDh7QyIIhk+VBJ/OGTJcLnawxtC7BDump0TkrUNhoW7kwrYITso0utWvkwSj2+R8AOKwnSe36AFzvbDdp18IJTgLDAHRwR7HXfLvUQkRERNJgdUgFgI4dO+K7776DVqtFVlYWAMDPzw9OTrXqxlUOYdS7KqFLhkJh2i0/FsUFyXBr0NKoRkf1JBV7zYc8+xTk2rs9vBqnINy+byXq500zCvpamQcKvdeLfh6JiIjIvqoUUvWcnJzg7+9v61ruObXhkqG+xqQbSQhrJs64rLLJXdsEA32hs/SCPhEREdlflUJqbm4ufvrpJ1y+fBk5OTnQ6YznXMlkMixdutSmBVLdYC7Q14agT0RERLZndUjdv38/nnzySeTn58PT0xPe3t4m+1hz21QiIiIiospYHVL/+9//wsfHB9u2bTNMkCIiIiIisgerZzxdvHgRU6dOZUAlIiIiIruzOqQqFAoUFxfbsxYiIiIiIgBVCKkzZszAF198gZycHHvWQ0RERERk/ZjUa9euoWHDhujWrRtGjhyJoKAgyOVyo31kMhleeuklmxdJRERERHWL1SH1rbfeMvz/F198IbgPQyoRERER2YLVIfWvv/6yZx1ERERERAZWh9TmzZvbsw4iIiIiIgOrJ04RERERETmK2Z7UyMhIODk5YePGjXB2dsawYcMqPZhMJsOWLVtsWiARERER1T1mQ6pOp4NWqzX8rNVqK73tqU6ns11lVCMytQpu+bFw0mRAKw9EsacSOmeF2GURERERWcVsSN22bZvFn0m6ZGoVPG5GQa5JKWsoBeSliShsGG82qLrK0uCes1AyoZYhm4iIqG6zeuIU1R5u+bF3A+q/5JoUuOXHoshnlcn+MrUKrd2nwLU4s6yhFJCXHEGh7zZRgqFMrYJH9lDItamGepyLt0Lr3B5a52AGViIiojqg2iH1wIEDWL9+PTIzM9GqVStMmTIFzZo1s2VttZ5YvYFOmgwz7ZmC7W55c+DqZLxNrk2FW94cFDX81ub1VcYtb87dgPovJxTBSZ0IqBMr7RUmIiKi2s9iSF2wYAE++ugjnDlzBv7+/ob2devW4cUXXzSMQd29ezfWr1+PX3/9tU4tVWUphApdcncp3g6NvA20Li3tGli18kCgVKg9AE7Fh1A/5znIkAUZZNA6+cBJmy14HJc7v6BYrXJ4GHQuOW5xu6VeYSJ74RAUIiLHsrgE1YEDBzBw4ECjgHrnzh3MmTMHXl5e2Lx5M1JTU7FmzRoUFBTg448/tnvBUqEPoa7FG+BcehCuxRvgcTMKMrUKgPAldxkK4aw5UbZv9lC4Z4+Dx41IuOfEGB5nC8WeSmjkwUZtGnkwSlyHoEHOMMiRASeoIUMp5NrrkEEj/G9EKTxuDLVpbbZirleYyB4q+30nIiLbsxhSk5OTER4ebtS2f/9+5OfnY9q0aejbty88PDwwcuRIjBkzBvv27bNnrZJiadwnYP6Su2FfbSpcS3bY5QNP56xAYcN4lLhFQ+3SByVu0ShsGA/3grchg7byA5SvU5cKt1uzbVKXtdQu4ZXuo5UHOKASojKV/b4TEZHtWQypOTk5CAgwDgMHDhyATCbD4MGDjdq7dOmCzMy607tlLoQ639kHjxuRkGmuVOl4tv7A0zkrUOSzCoWNEgyXxWXa9Gody7k00WZ1WaP4vgWwtJiZDs644z7BUeUQVXmcNxER1ZzFkNq4cWOkpxsHmyNHjqBBgwbo0KGD8YGcnODq6mr7CiVKKw8UbHfSZcG59CDk2isWg5bgY+30gae/VOkEdfUOoKvm46pJ56xAqWt/s9tlUMMjd4LNh0kQmWPu9509+kRE9mMxpHbr1g3ffvstcnNzAQBnzpzByZMn0bdvX5OF/S9cuICmTZvarVCpERr3WZHlWx+YstcHntClyqrQObnbsBrrFN+3GBr4m93upMviuEByCJlaBegKoUM9o3aNvGw5NCIisg+LIfX1119HZmYmunXrhkceeQSPPPIIZDIZXn75ZaP9dDodtm7diu7du9u1WCmpOO5TK/Or2fHgYbcPvMrGx1ZG5+T4Lx86ZwU0rm0r3Y/jAsmeDBOm7myHDHcAADq4ocQ1gsugERHZmcWQ2r59e2zevBnh4eG4ceMG/vOf/2Djxo144IEHjPY7cOAAGjRogOHDh9u1WKkpP+5TXa9/jY6lkbe175JUNXm8cwvbFFIFMrUKLiVHrNqX4wLJXoRX6SgGnBowoBIR2Vmli/n36NED69evt7hP3759cfjwYZsVVRsVeyohL02s9mV1rYvloQM1UeyphEvxdshQWOm+OngY7SfGJU1975W+56oyHBdI9sIJU0RE4rHYk0rWK3/5Xwsvs/tp4Q4djCeY2TsI6pwV0MjbVLqfRh6MAp/1JktXObrHqCpjaDkukOyJE6aIiMRT7duikin95X+PG5FwKj1osl0r80NBo90A8O+dazKhlQc45M41WpeWgOaESXtyqg8KS5qiSbMguPjFlf0b3HrbtZbKWBpDq4E/NK7d4KQrcNi5o7pL6AoJvxgRETkGQ6odmLstqbpef0OgcvQtPYs9ldAVHUM92d2Z8BdVDTFx3gws++wppNy5hjCJhD1z50/j1ByFvgkMpeQw+iskjv5SSUREDKl2IcXeF52zAncab8HtzHlIVV1ExnUvbD78JJZ9NhQKhReSkq6JVltF5s4fZ1OTGPRXSIiIyLEYUu1Aqr0vOmcFnIK+RPMgoDmA7iNFLccsqZ4/IiIichyGVDth70vN8PwRERHVbZzdT0RERESSw5BKRERERJLDkEpEREREksOQSkRERESSw5BKRERERJLDkEpEREREksOQSkRERESSw5BKRERERJLDkEpEREREksOQSkRERESSw5BKRERERJLDkEpEREREksOQSkRERESSw5BKRERERJLDkEpEREREksOQSkRERESSw5BKRERERJLDkEpEREREklMrQurq1avRqVMn+Pv7o1+/fjh8+LDYJRERERGRHUk+pG7cuBGzZ8/Gq6++it9++w3/+c9/EB0djatXr4pdGhERERHZiSw3N1cndhGWPPTQQ2jfvj3+97//Gdq6deuGESNGYN68eSJWRkRERET2Iume1JKSEvz5558YOHCgUfvAgQPx+++/i1QVEREREdmbpENqdnY2NBoN/Pz8jNr9/Pxw/fp1kaoiIiIiInuTdEjVk8lkRj/rdDqTNiIiIiK6d0g6pPr6+kIul5v0mt64ccOkd5WIiIiI7h2SDqmurq7o0qUL9u7da9S+d+9edO/eXaSqiIiIiMjenMUuoDIvvPACJk+ejPvvvx/du3fHmjVrkJmZiYkTJ4pdGhERERHZiaR7UgFg1KhRmD9/Pj744AP06dMHR48exfr169G8eXPDPlzsv3o+/vhjDBgwAM2aNUNISAjGjh2Lc+fOiV1WrfTRRx/B29sbr7/+util1BqZmZmYMmUKQkJC4O/vj+7du+PgwYNil1UraDQaxMbGGv7uderUCbGxsVCr1WKXJkmHDh3CY489hrZt28Lb2xvr1q0z2q7T6TB//ny0adMGAQEBGDp0KP7++2+RqiUiPcmHVAB47rnncPr0aVy/fh379+9H7969Ddu42H/1HTx4EM8++yx27dqFLVu2wNnZGVFRUcjJyRG7tFrl+PHjWLt2Ldq3by92KbVGbm4uBg8eDJ1Oh/Xr1+P333/HwoULOdbcSp988glWr16NuLg4HDt2DAsWLMCqVavw8ccfi12aJBUWFqJdu3ZYsGAB3N3dTbYvXrwYy5YtQ1xcHPbs2QM/Pz+MHDkS+fn5IlRLRHqSX8y/Mlzs33YKCgrQvHlzrFu3DhEREWKXUyvcunUL/fr1w+LFi7Fw4UK0a9cOH3zwgdhlSd4777yDQ4cOYdeuXWKXUiuNHTsWPj4+WLFihaFtypQpyMnJwQ8//CBiZdLXtGlTLFy4EOPHjwdQ1ovapk0bxMTE4LXXXgMAFBUVISwsDO+++y6HlhGJqFb0pJrDxf5tq6CgAFqtFt7e3mKXUmu88sorGDFiBPr16yd2KbXKtm3bcP/992PixIkIDQ3Fgw8+iM8++ww6Xa3+zuwwPXr0wMGDB/HPP/8AAM6fP48DBw7g//7v/0SurPZRqVS4du2a0eeIu7s7evXqxc8RIpFJfuKUJVzs37Zmz56Njh074j//+Y/YpdQKa9euRXJyMlauXCl2KbXO5cuX8fnnn+P555/HK6+8gtOnT2PWrFkAgEmTJolcnfS98sorKCgoQPfu3SGXy6FWq/Haa6/hueeeE7u0WufatWsAIPg5kpGRIUZJRPSvWh1S9bjYf83997//xdGjR7Fz507I5XKxy5G8pKQkvPPOO9ixYwdcXV3FLqfW0Wq16Nq1q2FITufOnZGcnIzVq1czpFph48aN+P7777F69Wq0adMGp0+fxuzZs9G8eXM89dRTYpdXK/FzhEh6anVI5WL/tjFnzhxs3LgRCQkJaNGihdjl1ArHjh1DdnY2evbsaWjTaDQ4fPgw1qxZg/T0dNSrV0/ECqXN398frVu3Nmpr1aoVUlNTRaqodpk7dy6mTZuG0aNHAwDat2+Pq1evYtGiRQypVeTv7w8AuH79OoKCggzt/BwhEl+tHpPKxf5rbtasWfjxxx+xZcsWtGrVSuxyao2hQ4fi8OHDOHDggOG/rl27YvTo0Thw4AB7VyvRo0cPXLx40ajt4sWLaNasmUgV1S63b982ueIhl8uh1WpFqqj2UigU8Pf3N/ocKS4uxpEjR/g5QiSyWt2TCnCx/5p47bXX8MMPP+Cbb76Bt7e3YWyWh4cHGjRoIHJ10ubt7W0ywax+/frw8fFBu3btxCmqFnn++efx8MMP48MPP8SoUaNw6tQpfPbZZ3jzzTfFLq1WGDJkCD755BMoFAq0adMGp06dwrJly/DYY4+JXZokFRQUIDk5GUDZUJPU1FScOnUKPj4+aNasGaZOnYqPPvoIYWFhCA0NxYcffggPDw88+uijIldOVLfV+iWogLLF/BcvXoxr166hbdu2eP/9943WUiVh5mbxz5o1C3PmzHFsMfeAoUOHcgmqKti1axfeeecdXLx4EUFBQYiJicHkyZM5DtAK+fn5eO+997B161bcuHED/v7+GD16NGbOnAk3Nzexy5OcAwcOYNiwYSbt48aNw/Lly6HT6bBgwQJ8+eWXyM3Nxf33348PP/yQXziJRHZPhFQiIiIiurfU6jGpRERERHRvYkglIiIiIslhSCUiIiIiyWFIJSIiIiLJYUglIiIiIslhSCUiIiIiyWFIpVqnY8eOmDp1qijPfeDAAXh7e+PAgQM2Pe7UqVMNt2esK4YOHYqhQ4fa/LhFRUVo27Yt1q5da2hbt24dvL29oVKpDG1Tp05Fx44dbf78YhB6Xz711FO8qQkR1WoMqSQ6fYAo/19ISAgiIiKwefNmscurkfz8fHz44Yfo168fmjVrBn9/f4SHh+P111/HpUuXxC7P7o4cOYL58+cjNzfXYc/52WefQSaTYdy4cVV+7AcffICtW7eatJ87dw7z5883CrlSN336dMTHx+PUqVNil0JEVC0MqSQZs2fPxsqVK7FixQq88soryM/Px9NPP40ff/xR7NKq5fLly+jbty/ef/99BAcHQ6lU4oMPPsDgwYOxdetW9OjRQ+wS7e7o0aOIi4vDrVu3TLZt2rQJmzZtsunzqdVqfPrpp3jiiSfg6upqaH/ssceQmZmJ5s2bG9r+97//ITEx0ejxH374IbZt22Zy3L///htxcXG4cuWKTeu1p65du6Jz585YunSp2KUQEVWLs9gFEOk99NBDeOCBBww/T5gwAa1bt8aPP/5Y6+6hrVar8cQTTyAzMxNbtmzBgw8+aLT9zTffxDvvvGOT59LpdLhz506tux1m+RBpK7/88guuXbuG0aNHG7XL5XLI5XKjNhcXF5s/f1Xdvn0b9evXt9vxR40ahfnz5yMvLw9eXl52ex4iIntgTypJlqenJ+rXr19pmCgpKcF7772H/v37Q6FQICAgAA899BC2b99usq+3tzemT5+OX375BX369IG/vz+6desm2FublJSEUaNGITAwEK1atcKbb76J0tJSq2rfsmULzpw5gxkzZpgEVABwc3PD+++/b9J+/fp1TJw4Ec2aNYNCocDLL7+M4uJiwX9DfHw8evXqhcaNG+Onn34CAFy9ehUxMTFo2bIl/P398eCDD+K7774zerxKpYK3tzcWLVqEtWvXomvXrggMDMSwYcNw+fJlAMDSpUvRsWNHBAQEYPTo0cjMzDQ6xuHDhzFhwgR06NABjRs3Rps2bfDKK68YXdafP38+3n77bQBA586dDUM59OMmK45JLV/Xd999hwceeACNGzdGr169sG/fPqvO+9atWxEYGIjWrVsbtVszJtXb2xt37tzBd999Z6h16NChWLduHZ599lkAwLBhwwzb1q1bZ3jsyZMnMXbsWDRv3hwBAQEYOHAgdu7cKVjDb7/9htmzZ6NVq1Zo0qRJlY4BVO192a9fPxQVFWHPnj1WnT8iIilhTypJRl5eHrKzswEAWVlZWLNmDbKzs/HYY49ZfFx+fj6++OILjBw5Ek888QSKioqwYcMGjB8/Hj/++CMeeugho/2PHz+Obdu2YeLEiXjyySfx1VdfYdKkSejYsaMh3GRlZWHo0KEoKirCCy+8gIYNG+L777/H3r17rfq37NixAwAqrb08rVaLkSNHon379nj77beRmJiItWvXwtfXF3PnzjXa98iRI9i8eTNiYmLg7++PVq1aITs7G0OGDEFOTg4mTZqEgIAAbNy4EVOnTkVubq7JZLNNmzahqKgIzzzzDAoKCrB48WKMHz8eo0ePxpYtW/D8888jMzMTS5cuxYwZM/Dtt98aPTYnJwdPPfUU/P39cebMGXz11Vf4+++/sWvXLgBlgS4pKQkbN27E+++/D19fXwAwCZAVbd68GdnZ2Zg4cSLc3NywfPlyPPHEEzh9+jR8fHwsPvbo0aPo0qWLtafcyMqVKzFt2jSEh4djwoQJAIDGjRsjODgYMTExWLVqFV599VW0atUKANC9e3cAwMGDBzF69Gi0a9cOr7/+OlxdXbFp0yaMGzcOa9euxfDhw42eZ9asWbjvvvswY8YM5OXlVekYVX1ftm/fHm5ubjhy5AiioqKqdV6IiMTCkEqSUfESrYuLCxYtWlTpDHBvb2+cPXsW9erVM7RNnjwZffr0wZIlS0xC6vnz53Ho0CFDWIqKikKHDh3wzTff4N133wUAfPLJJ7h+/Tq2b9+OXr16ASgbfiDUKyrkwoUL8PLyQrNmzazaHwBKS0sREREBpVIJAHjmmWeQm5uLtWvXmoTUCxcuYP/+/ejUqZOhTalUIi0tDZs3b0a/fv0Mx4iIiEBsbCwef/xx3HfffYb9U1NT8ccff8Db2xsA4OTkhPnz56O4uBiHDx82nM+CggKsWbMGN27cQKNGjQAAb7/9tsll6vDwcEyePBlHjx5Fjx490KFDB3Ts2BEbN27E0KFDoVAorDoPKSkpOHHihOG5HnzwQfTt2xc//vgjYmJizD5OrVYjOTkZ//d//2fV81Q0duxYvPTSS2jRogXGjh1rtK1Hjx5YtWoV+vfvjz59+hjadTodpk+fjv/85z/YvHkznJzKLk7FxMRg8ODBmDt3rklIrV+/PrZu3QpnZ+cqH6Oq70tnZ2c0bdoU//zzT7XOCRGRmHi5nyQjLi4O8fHxiI+Px2effYYBAwbg1VdfrXSGv1wuNwSqkpIS5OTkID8/H71798aff/5psn+fPn2MevMaN26MsLAww6VuANi1axc6d+5sCAJAWbjQ97BVJj8/H56enlbtW57+srJe7969kZ2djfz8fKP27t27GwVUfc2dOnUyBFSgbNzn1KlTUVhYiIMHDxrtP3z4cENABcpCJgA8+uijRoH//vvvh06nM7pUrg+oOp3O0AOu71kUOudVERUVZQioANCpUyd4eXkZvT5CcnJyoNPpjP5N9nb69GkkJSVhzJgxyMnJQXZ2NrKzs5GTk4NBgwbh8uXLJpOtnn76aUNAreoxqvO+9PHxMVyhICKqTdiTSpLRrVs3o4lTjz76KPr164eZM2ciIiLC4kSbr776Cp9++ikuXLgAnU5naJfJZCb7CvVuent7Iycnx/Dz1atXMWzYMJP9QkNDrfq3eHp6VhqqKnJxcUFgYKBJXUBZACsfelu0aGHy+CtXrgjWrA/kFcNSUFCQ0c/6iTVNmzYVbC8/3jQ1NRVz587FL7/8YhKghWbyV4XQ63PfffcZvT6WlH/97U2/jNiLL76IF198UXCfGzduGK0qUPG1q8oxqvO+1Ol0gr8HRERSx5BKkuXk5IQHH3wQy5cvx6VLl9C2bVvB/X788Ue89NJLiIiIwMsvvww/Pz84Oztj3bp12LBhg8n+FWd561UMN0If7NYGoNatW+PUqVNITU01CYPm6C/zWlObu7u7VccUeqyeufNQ2fnRarUYNWoUbty4genTp6NVq1bw8PCAVqvF6NGjodVqra6tOs9vTsOGDSGTyRy6Jqv+3/rWW2+ZHQtbMUBWfO2qeoyqvi9zc3OtHmpBRCQlDKkkaWq1GgBQWFhodp+NGzeiRYsW+Pbbb40+wMvPvq6qZs2aCY7js3YB/oiICGzYsAHff/89XnvttWrXURXNmzcXrDkpKcmw3RbOnDmDf/75B59++ikef/xxQ7vQuXFkD55cLkdISEiNFtw3V6+59uDgYABAgwYN0L9//2o9Z1WOUdX3ZWlpKdLS0qo9TpeISEwck0qSVVpair1798LV1dUwo1qIvuetfG/S5cuXBe8cZK2HH34Yf/31Fw4fPmxou337Nr788kurHj98+HB06NABH3/8MY4cOWKy/c6dO3jjjTeqXZ+QwYMH49SpU/jtt98MbaWlpVixYgXq169v9aSvygidbwBYsmSJyb76sauO6t3s3r17jcbE1q9fX7BWc/+OLl26ICQkBEuWLBEc5nDjxo1Kn7Mqx6jq+/Ls2bMoLi42jBcmIqpN2JNKkvHrr78iOTkZQNlSOxs3bsTFixcxffp0iwuRR0REICEhAePGjUNERATS09Px+eefIyQkBGfOnKlWLa+88grWr1+Pxx57DJMmTTIs9WPtwuvOzs745ptvEBUVhcjISAwfPhy9evVCvXr1cPHiRWzcuBHXr1/He++9V636hEyfPh0bN27EuHHjMHnyZPj7+2PTpk04fvw43n//faOZ/TXRqlUrhISEQKlUIj09HT4+Pvjll1+Qnp5usm/Xrl0BAO+++y5Gjx4NV1dX9O3bF35+fjappaJHHnkE69atw99//212eIglXbt2xf79+7FkyRI0adIEjRo1Qr9+/dC5c2c4OTlh0aJFuHXrFtzd3XH//fejRYsWWLp0KUaPHo0ePXpg/PjxaN68OTIzM3H8+HFcvXoVR48etficTk5OVh+jqu/Lffv2wd3dHQMHDqzyuSAiEhtDKknGggULDP/v5uaGsLAwfPzxx5g4caLFxz3++OO4ceMGPv/8c+zbtw8tW7bE+++/j+Tk5GqH1MaNG2Pbtm2YNWsWli5dCk9PT4wdOxYDBw7EqFGjrDpGixYt8Ntvv2HlypXYsmULfv75Z6jVajRr1gxDhw41Wbe0pnx9fbFr1y68/fbb+OKLL3D79m2EhoZi+fLl1bqPvTkuLi74/vvvMXv2bCxZsgROTk4YNGgQfvrpJ5Me7wceeABKpRJffvklXnjhBWi1WiQkJNgtpA4ePNhwcwP9Ul5VsWDBAsyYMQMLFixAYWEhevfujX79+iEwMBCffPIJPvnkE7z88svQaDRYtmwZWrRogZ49e+LXX3/FwoUL8eWXXyIvLw9+fn7o0KED5syZY9XzWnuMqr4v4+PjERkZabMvKEREjiTLzc113FRYIiI7++STT7By5Ur8+eefhqW0vvrqK7z00ks4e/asyeoF96qTJ09i4MCB2LdvHzp37ix2OUREVcYxqUR0T5k8eTIAGN0O9tq1a5DJZJXesepesmjRIowYMYIBlYhqLfakEtE96/r169i8eTMWLVqEZs2aGW7ZSkRE0seeVCK6Z124cAFz585FixYt8Omnn4pdDhERVQF7UomIiIhIctiTSkRERESSw5BKRERERJLDkEpEREREksOQSkRERESSw5BKRERERJLz/0gsuuG5UwxJAAAAAElFTkSuQmCC\n", "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "jwc_darkblue = jwc[jwc['Color'] == 'darkblue']\n", "jwc_gold = jwc[jwc['Color'] == 'gold']\n", "\n", "fig, ax = plt.subplots(figsize=(7,6))\n", "\n", "ax.scatter(jwc_darkblue['Bland Chromatin (jittered)'], \n", " jwc_darkblue['Single Epithelial Cell Size (jittered)'], \n", " label='Color=darkblue', \n", " color='darkblue')\n", "\n", "ax.scatter(jwc_gold['Bland Chromatin (jittered)'], \n", " jwc_gold['Single Epithelial Cell Size (jittered)'], \n", " label='Color=gold', \n", " color='gold')\n", "\n", "x_label = 'Bland Chromatin (jittered)'\n", "\n", "y_label = 'Single Epithelial Cell Size (jittered)'\n", "\n", "plt.ylabel(y_label)\n", "\n", "plt.xlabel(x_label)\n", "\n", "ax.legend(bbox_to_anchor=(1.04,1), loc=\"upper left\")\n", "\n", "plt.xlim(0, 11)\n", "plt.ylim(0, 11);\n", "\n", "plt.show()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "For instance, you can see there are lots of samples with chromatin = 2 and epithelial cell size = 2; all non-cancerous.\n", "\n", "Keep in mind that the jittering is just for visualization purposes, to make it easier to get a feeling for the data. We're ready to work with the data now, and we'll use the original (unjittered) data." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "First we'll create a training set and a test set. The data set has 683 patients, so we'll randomly permute the data set and put 342 of them in the training set and the remaining 341 in the test set." ] }, { "cell_type": "code", "execution_count": 13, "metadata": {}, "outputs": [], "source": [ "shuffled_patients = patients.sample(683, replace=False) \n", "training_set = shuffled_patients.take(np.arange(342))\n", "test_set = shuffled_patients.take(np.arange(342, 683))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Let's stick with 5 nearest neighbors, and see how well our classifier does." ] }, { "cell_type": "code", "execution_count": 14, "metadata": {}, "outputs": [ { "data": { "text/plain": [ "0.967741935483871" ] }, "execution_count": 14, "metadata": {}, "output_type": "execute_result" } ], "source": [ "evaluate_accuracy(training_set, test_set, 5)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "Over 96% accuracy. Not bad! Once again, pretty darn good for such a simple technique.\n", "\n", "As a footnote, you might have noticed that Brittany Wenger did even better. What techniques did she use? One key innovation is that she incorporated a confidence score into her results: her algorithm had a way to determine when it was not able to make a confident prediction, and for those patients, it didn't even try to predict their diagnosis. Her algorithm was 99% accurate on the patients where it made a prediction -- so that extension seemed to help quite a bit." ] } ], "metadata": { "anaconda-cloud": {}, "kernelspec": { "display_name": "Python 3", "language": "python", "name": "python3" }, "language_info": { "codemirror_mode": { "name": "ipython", "version": 3 }, "file_extension": ".py", "mimetype": "text/x-python", "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", "version": "3.8.5" } }, "nbformat": 4, "nbformat_minor": 1 }